Нажмите кнопку OK в диалоговом окне Добавить ограничение. Диалоговое окно Параметры поиска решения должно выглядеть, как на следующем рисунке.

7. В диалоговом окне Параметры поиска решения, открываемом нажатием кнопки Параметры в диалоговом окне Параметры поиска решения, введем ограничение, что все изменяемые ячейки – неотрицательны.

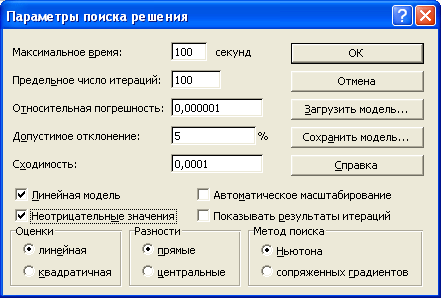
Выберите параметры Линейная модель и Значения не отрицательны, а затем нажмите кнопку "OK".

Что означает выбор этих параметров?

Выбор параметра Значения не отрицательны гарантирует, что надстройка "Поиск решения" будет рассматривать только такие комбинации изменяемых ячеек, в которых значение каждой изменяемой ячейки будет неотрицательным.

Мы выбрали Линейная модель, так как проблема номенклатуры продуктов – это специальный тип проблемы поиска решений, называемый линейной моделью. По существу, модель поиска решений является линейной при следующих условиях:

• Целевая ячейка вычисляется путем сложения членов формы (изменяемая ячейка)*(константа).

• Все ограничения удовлетворяют требованиям линейной модели. Это означает, что каждое ограничение оценивается путем сложения членов формы (изменяемая ячейка)*(константа) и сравнения этих сумм с константой.

Почему эта проблема поиска решения линейна?

Наша целевая ячейка (прибыль) вычисляется следующим образом:

(Прибыль на килограмм лекарства 1) *

(Произведенные килограммы лекарства 1) +

(Прибыль на килограмм лекарства 2) *

(Произведенные килограммы лекарства 2) +

...

(Прибыль на килограмм лекарства 6) *

(Произведенные килограммы лекарства 2)

Этот расчет соответствует модели, в которой значение целевой ячейки получается путем сложения членов формы (изменяемая ячейка)*(константа).

Наше ограничение на трудовые ресурсы оценивается путем сравнения доступных трудовых ресурсов со значением, рассчитываемым следующим образом:

(Трудозатраты для производства килограмма лекарства 1)*

(Количество килограммов лекарства 1) +

(Трудозатраты для производства килограмма лекарства 2)*

(Количество килограммов лекарства 2) +

...

(Трудозатраты для производства килограмма лекарства 6)*

(Количество килограммов лекарства 6)

Следовательно, ограничение на трудовые ресурсы оценивается путем сложения членов формы (изменяемая ячейка)*(константа) и сравнения этих сумм с константой. Оба ограничения, на трудовые ресурсы и на исходные материалы, удовлетворяют требованиям линейной модели.

Наше ограничение на спрос принимает следующий вид

(Произведенное лекарство 1)<=(Спрос на лекарство 1)

(Произведенное лекарство 2)<=(Спрос на лекарство 2)

...

(Произведенное лекарство 6)<=(Спрос на лекарство 6)

Все ограничения на спрос удовлетворяют требованиям линейной модели, так как каждое из них оценивается путем сложения членов формы (изменяемая ячейка)*(константа) и сравнения этих сумм с константой.

Почему важно показать, что наша модель номенклатуры продуктов является линейной?

• Если модель поиска решения линейна, и выбран параметр Линейная модель, то надстройка "Поиск решения" гарантированно найдет оптимальное решение для соответствующей модели. Если модель поиска решения не является линейной, надстройка "Поиск решения" может найти оптимальное решение, а может и не найти.

• Если модель поиска решения линейна, и выбран параметр Линейная модель, надстройка "Поиск решения" использует очень эффективный алгоритм (симплексный метод), чтобы найти оптимальное решение для модели. Если модель поиска решения линейна, но параметр Линейная модель не выбран, надстройка "Поиск решения" использует очень неэффективный алгоритм (метод GRG2) и может испытывать трудности при поиске оптимального решения модели.

8. Нажав кнопку OK в диалоговом окне Параметры поиска решения, мы возвращаемся в основное диалоговое окно Поиск решения. После нажатия кнопки Выполнить надстройка "Поиск решения" вычисляет оптимальное решение (если оно существует) для нашей модели номенклатуры продуктов.

Оптимальное решение для модели номенклатуры продуктов представляет собой набор значений изменяемых ячеек (количество произведенных килограммов каждого продукта), который обеспечивает прибыль, максимальную из набора всех подходящих решений. И снова, под термином подходящее решение понимается набор значений изменяемых ячеек, удовлетворяющий всем ограничениям. Значения изменяемых ячеек, показанные на рис. 2, – это подходящее решение, так как все уровни производства неотрицательны, ни один из уровней производства не превышает спроса, и используемые ресурсы не превышают доступные ресурсы.

Рис. 2. Подходящее решение проблемы номенклатуры продуктов, учитывающее ограничения.

Значения изменяемых ячеек, приведенные на рис. 3, представляют собой недопустимое решение по следующим причинам:

• Уровень производства лекарства 5 превышает спрос.

• Используемые трудовые ресурсы превышают доступные.

• Используемые исходные материалы превышают доступные.

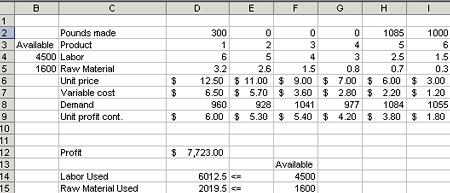
Рис. 3. Недопустимое решение проблемы номенклатуры продуктов не удовлетворяет заданным ограничениям.

После нажатия кнопки Выполнить надстройка "Поиск решения" быстро находит оптимальное решение, показанное на рис. 4. Чтобы сохранить значения оптимального решения в электронной таблице, необходимо нажать кнопку Сохранить найденное решение.

Рис. 4. Оптимальное решение проблемы номенклатуры продуктов.

Наша фармацевтическая компания может обеспечить ежемесячную максимальную прибыль на уровне 6625,20 руб., производя 596,67 килограммов лекарства 4, 1084 килограммов лекарства 5, и не производя никаких других лекарств! Мы не можем определить, можно ли добиться максимальной прибыли 6625,20 руб. другими способами. Можно гарантировать только, что с нашими ограничениями со стороны спроса и ресурсов не существует способа получить ежемесячную прибыль, превышающую 6625,20 руб.

Всегда ли надстройка "Поиск решения" находит решение?

Пусть должен быть удовлетворен спрос на каждый продукт. При этом понадобится изменить наши ограничения на спрос с D2:I2 <= D8:I8 на D2:I2 >= D8:I8. Чтобы изменить это ограничение:

1. Откройте надстройку "Поиск решения".

2. Щелкните ограничение D2:I2 <= D8:I8, а затем нажмите кнопку Изменить.

Появится диалоговое окно Изменить ограничение.

3. В центральном поле выберите >=, а затем нажмите кнопку OK.

Теперь надстройка "Поиск решения" будет рассматривать только те значения изменяемых ячеек, которые удовлетворяют спрос на все лекарства.

После нажатия кнопки Выполнить появится сообщение Поиск не может найти подходящего решения. Это сообщение означает, что при наших ограниченных ресурсах нельзя удовлетворить спрос на все продукты. В нашей модели нет никакой ошибки! Надстройка "Поиск решения" просто информирует, что если нужно удовлетворить спрос на все продукты, требуется увеличить доступные трудовые ресурсы, исходные материалы, или и то, и другое.

Что означает, если заданные значения не сходятся к решению?

Посмотрим, что произойдет, если позволить неограниченный спрос на каждый продукт и допустить возможность производства отрицательного количества каждого лекарства. Чтобы найти оптимальное решение для этой ситуации, выполните следующие действия:

1. Откройте надстройку "Поиск решения".

2. Нажмите кнопку Параметры, и затем снимите флажок Значения не отрицательны.

3. В диалоговом окне Параметры поиска решения щелкните ограничение на спрос D2:I2 <= D8:I8, а затем нажмите кнопку Удалить для удаления ограничения.

После нажатия кнопки Выполнить надстройка "Поиск решения" вернет сообщения Значения целевой ячейки не сходятся. Это сообщение означает, что, если должно быть получено максимальное значение (как в нашем случае), существуют подходящие решения со сколь угодно большими значениями целевой ячейки. (Если целевая ячейка должна быть минимизирована, это сообщение означает, что существуют подходящие решения со сколь угодно малыми значениями целевой ячейки.)

В нашем случае, разрешив отрицательные количества лекарств, мы фактически "создаем" ресурсы, которые могут быть использованы для производства сколь угодно больших количеств других лекарств. В условиях неограниченного спроса это позволяет получить неограниченную прибыль. В реальной ситуации невозможно получить неограниченные суммы денег. Вкратце, если появляется сообщение Значения целевой ячейки не сходятся, то ваша модель содержит ошибку.

Проверьте себя

Решения этих проблем содержатся в файлах с s25_1.xls по s25_5.xls, включенных в набор загружаемых файлов примеров.

1. Пусть наша фармацевтическая компания может приобрести до 500 человеко-часов с ценой 1 руб. за час. Получит ли она преимущество от этой возможности?

2. На фабрике по производству микросхем четыре техника (A, B, C и D) производят три продукта (продукты 1, 2 и 3). Производитель микросхем может продать в этом месяце 80 единиц продукта 1, 50 единиц продукта 2 и, самое большее, 50 единиц продукта 3. Техник A может производить только продукты 1 и 3. Техник B может производить только продукты 1 и 2. Техник C может производить только продукт 3. Техник D может производить только продукт 2. Каждая произведенная единица продукта дает следующую прибыль: продукт 1: 6 руб.; продукт 2: 7 руб.; продукт 3: 10 руб. Время (в часах), требуемое каждому из техников для производства продукта, показано в следующей таблице.

   Продукт	Техник A	Техник B	Техник C	Техник D
   1	2	2,5	Не может	Не может
   2	Не может	3	Не может	3,5
   3	3	Не может	4	Не может

4. Каждый техник может работать до 120 часов в месяц. Как производитель микросхем может добиться максимальной ежемесячной прибыли?

5. Завод по производству компьютеров производит мыши, клавиатуры и джойстики для видеоигр. Прибыль на единицу продукта, трудозатраты на единицу продукта, ежемесячный спрос и машинное время на единицу продукта приведены в следующей таблице:

   	Мыши	Клавиатуры	Джойстики
   Прибыль на единицу	8 руб.	11 руб.	9 руб.
   Трудозатраты на единицу	0,2 часа	0,3 часа	0,24 часа
   Машинное время на единицу	0,04 часа	0,055 часа	0,04 часа
   Ежемесячный спрос	15 000	25 000	11 000

7. Каждый месяц суммарно доступно 13000 человеко-часов и 3000 часов машинного времени. Как производитель может получить максимальную прибыль от своей фабрики?

8. Рассмотрим снова наш пример с лекарствами, предположив, что для каждого лекарства должен быть удовлетворен минимальный спрос в 200 единиц.

9. Ювелир Петров делает бриллиантовые браслеты, ожерелья и серьги. Он хочет работать не больше 160 часов в месяц. У него есть 800 унций бриллиантов. Прибыль, время работы и количество бриллиантов в унциях, необходимые для производства каждого продукта, приведены ниже. Если спрос на все продукты неограничен, как может Петров максимизировать свою прибыль?

12