23.Энтропия

«Недостатки» W - огромные числа, не обладает аддитивностью. Две подсистемы (не взаимодействующие) Þ W1, W2 Þ каждое из W1 1й подсистемы может совместно реализоваться с каждым из W2 2й подсистемы Þ W = W1W2 – различных комбинаций Þ lnW = lnW1 + lnW2 – аддитивная величина.

Характеристика вероятности состояния системы Þ s = lnW - энтропия системы – функция состояния термодинамической системы (f(p,V,T)).

Методы статистической физики Þ ds = d’Q/kT Þ приращение энтропии, обусловленное получением системой в ходе обратимого процесса количества теплоты d’Q.

Экспериментальная физика Þ S = ks = k ln W .

[S] = Дж/К, 1 моль О2 Þ s = 1,5·1025, S = 200 Дж/К.

dS = d’Q/T (для обратимых процессов).

Свойства энтропии (из определения):

1. В ходе необратимого процесса энтропия изолированной системы возрастает (из менее вероятных Þв более вероятные состояния, W растет, S растет).

2. Энтропия изолированной системы, находящейся в равновесном состоянии, максимальна. Утверждение, что энтропия изолированной системы может только возрастать либо по достижении максимального значения оставаться постоянной – закон возрастания энтропии или II начало термодинамики.

Изолированная система Þ d’Q = 0 Þ dS = 0 (обратимый процесс) Þ S = const Þ в ходе обратимого процесса в изолированной системе энтропия остается постоянной.

Протекание необратимого процесса в изолированной системе (d’Q = 0) сопровождается ростом энтропии (dS > 0) Þ d’Q в ходе необратимого процесса Þ кроме d’Q/Т положительное приращение, обусловленное необратимостью процесса Þ

dS > d’Q/T (необратимый процесс).

Т- температура теплового резервуара, от которого данная система получает количество теплоты d’Q.

Необратимый процесс в системе, отдающей теплоту внешней среде (d’Q < 0) Þ S может убывать, если │d’Q/Т│больше той доли приращения S, которая обусловлена необратимостью процесса.

Объединяя Þ dS ≥ d’Q/Т.

Обратимый процесс в неизолированной системе

dS > 0 (d’Q > 0) и dS < 0 (d’Q < 0).

Состояние, осуществляемое небольшим числом способов – упорядоченное или неслучайное.

Состояние, осуществляемое многими способами – беспорядочное или случайное Þ

Энтропия – мера степени беспорядка в системе.

Сообщение системе Q – усиление хаотического движения молекул Þ увеличение степени беспорядка.

Чем выше Т, тем больше внутренняя энергия, тем меньшим оказывается относительное возрастание беспорядка, обусловленного сообщением системе данного количества теплоты d’Q. При Т = ОК Þ всякое тело, как правило, в состоянии, статистический вес которого W = 1 Þ S = k lnW = 0 Þ

Энтропия любого тела стремится к 0 при стремлении к 0 температуры

limS = 0 – теорема Нернста (III начало термодинамики).

d’Q = TdS, аналогично d’A = pdV.

24.Физический смысл Энтропии.

Из рис. Þ 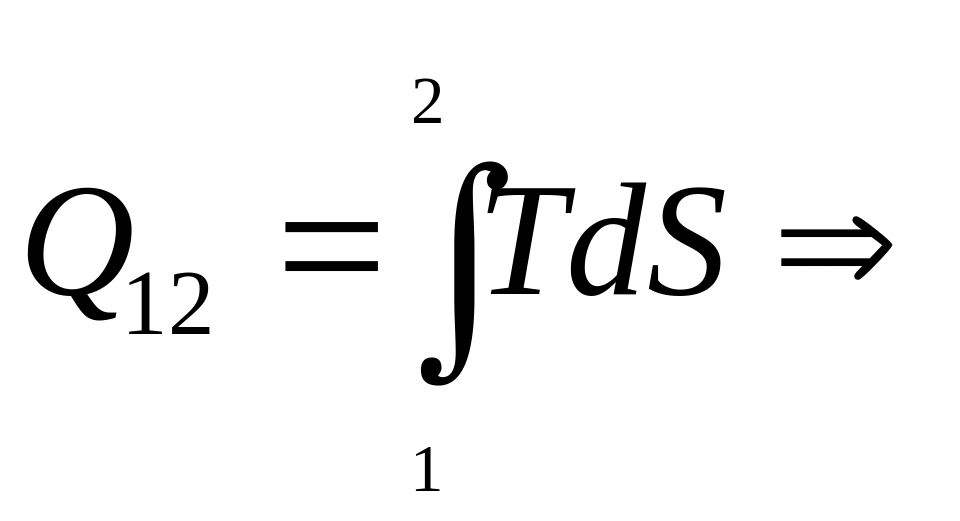изотермический процесс –

Q12 = T(S2 – S1) (A = p(V2 – V1)).

Круговой процесс Þ Q = площади цикла (аналогично для А).

I начало термодинамикиÞTdS = dU + pdV Þ dS = (dU + pdV)/T.

Для моля Þ UM = CvT, p/T = R/VM Þ

dSM = Cv · dT/T + R · dVM/VM Þ SM = Cv lnT + R lnVM + S0 (энтропия моля идеального газа, как функция Т и V). Перепишем Þ SM = Cv lnT + R lnR + R lnT – R lnp + S0 Þ идеальный газ – Cv + R = Cp Þ R lnR + S0 = S0’ Þ

SM = Cp lnT – R lnp + S0’ Þ (T = pV/R) Þ

SM = Cv lnp + Cv lnV – Cv lnR + R lnV + S0 Þ

Cv lnR + S0 = S0’’ Þ SM = Cv lnp + Cp lnV + S0’’.

Для массы m – умножить на m/M. Рассмотренный ранее пример с расширением газа Þ Δ’Q = 0,

U’ = const, T = const Þ V = 2V Þ

ΔS = R(ln 2V – lnV) = R ln2 (моль газа) Þ процесс необратим, энтропия увеличилась.

Физический смысл энтропии

Применим формулу

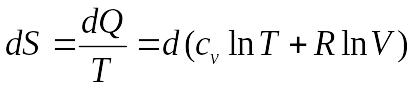
для вычисления изменения энтропии в изотермическом процессе Т=const, где энергетическое состояние газа остается неизменным, а всевозможные изменения характеристик обусловлены лишь изменением объема. Для этого случая

и, следовательно,

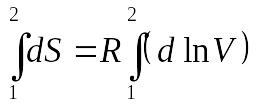
что после интегрирования дает

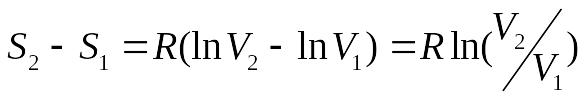
Определение. Состояние макроскопического тела, определенное так подробно, что заданы все состояния молекул, называется микросостоянием.Определение. Число разных микросостояний, соответствующих данному макросостоянию, называется статистическим весом или термодинамической вероятностью макросостояния. Т.о., статистический вес представляет собой число микроскопических способов, которым может быть осуществлено данное макросостояние. Чтобы пояснить понятие статистического веса, рассмотрим способы, которыми молекулы газа могут распределяться между двумя половинами сосуда, в котором находится газ.

Каждая молекула может находиться как в правой, так и в левой части сосуда. Поэтому вероятность того, что молекула 1 окажется в левой части равна 0.5. Пребывание молекул 1 и 2 в разных частях является статистически независимым событием. Поэтому вероятность одновременного нахождения молекул справа или слева равна 0.25 – произведению вероятностей.Обобщая результаты на объем V, состоящий из множества частей, который содержит NA молекул, получаем формулу для числа пространственных микросостояний