19.Адиабатический процесс

Обратимый процесс, идеальный газ Þ pV = m/M·RT. При некоторых процессах – один из параметров Þ const. Процесс, протекающий без теплообмена с внешней средой – адиабатический.

Для нахождения адиабаты используем I начало термодинамики в виде d’Q = d((m/M)·CvT) + pdV, т.к. теплообмена с внешней средой нет (d’Q = 0) Þ pdV = - (m/M)·CvdT, взяв дифференциал от обеих частей уравнения состояния идеального газа, получим:

pdV + Vdp = (m/M)·RdT, умножим предыдущее уравнение на R/Cv и сложим с последним Þ

g pdV + Vdp = 0, где g = 1 + R/Cv = Cp /Cv Þ

g·(dV/V) + (dp/p) = 0 Þ d(ln(pVg)) Þ

pVg = const – уравнение адиабаты, уравнение Пуассона.

pVg = pV·Vg-1 Þ TVg-1 = const.

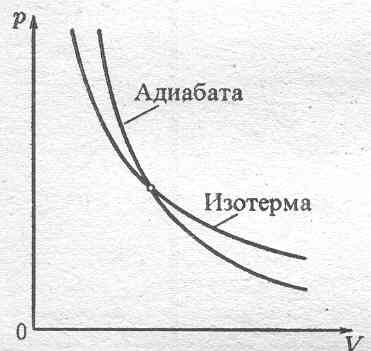
Вычислим dp/dV для изотермы и адиабаты в одной и той же точке.

Изотерма pdV + Vdp = 0; dp/dV = - p/V.

Адиабата pgVg-1dV +Vgdp = 0; dp/dV = - gp/V.

Таким образом, тангенс угла наклона касательной у адиабаты в g раз больше, чем у изотермы. Подразумевается, что процессы обратимые, т.е. бесконечно медленные, но для адиабатического процесса – невозможно Þ Приближение – быстропротекающие процессы Þ выполняется в пределах небольших V газа, в которых распространяется звуковая волна.

20.Политропический процесс

Политропические процессы – теплоемкость тела постоянна, т.е. кроме уравнения состояния – дополнительное условие C = const.

Идеальный газ, d’Q заменим Þ m/M·CdTÞ (m/M)·CdT = (m/M)·CvdT + pdV Þ

(m/M)·(C – Cv)RdT = RpdV. Получали Þ

(m/M)·RdT = pdV + Vdp Þ

(C – Cv)(pdV + Vdp) = RpdV Þ

(C – Cv - R)pdV + (C – Cv)Vdp = 0 Þ делим на pV.

(С – Ср)(dV/V) + (C – Cv)(dp/p) = 0 (Cp = Cv + R) Þ

Введем

уравнение политропы идеального газа. Можно Þ TVh-1 = const, n – показатель политропы. Найдем

C: Все рассмотренные ранее процессы – политропические.

Процесс	n	C
Изобарический Изотермический Адиабатический Изохорический	0 1 g ¥	Ср ¥ 0 Сv

21. Работа при изопроцессах.

Обратимый процесс, р = f(v), работа Þ

Изохорический процесс, V = const, dV = 0 Þ A = 0.

2. Изобарический процесс, p = const Þ A12 = p(V2 – V1).

3. Изотермический процесс, Т = const Þ

4. Адиабатический процесс, рVg = const, d’Q = 0 Þ d’A = - dU Þ A12 = -(U2 – U1) = U1 – U2 Þ подставим U = [1/(g-1)]pV Þ A12 = [1/(g-1)](p1V1 – p2V2) = [p1V1/(g-1)](1- p2V2/p1V1) Þ

5. Политропический процесс, pVn = const Þ

заменяем g на n

22.Обратимые и необратимые процессы

Свойства систем молекул не сводимы к свойствам отдельных молекул Þ состояние газа определяется только условием в данный момент времени и не зависит от начальных условий Þ отличие газа от механических систем (f(p,v,T) ≠ f(p,v,T,t).

Тепловые процессы в отличии

от механических (при отсутствии

трения) могут быть необратимыми.

Wp = mgh, т.е. чисто механическое движение обратимо.

При наличии теплового движения процессы, как правило, необратимые Þ например, торможение пули в воздухе Þ рассеянное тепло не превратить в механическую энергию. Вопрос: нельзя ли с помощью каких-либо процессов или механизмов добиться того, чтобы участвовавшие в них тела можно было вернуть в исходное состояние без того, чтобы в природе возникли какие-либо изменения?

Два типа необратимых процессов:

• расширение газа в пустоту;

• теплообмен между двумя телами.

Сосуд с перегородкой Þ идеальный газ и абсолютный вакуум V1 = V2 = V Þ убираем перегородку Þ Vгаза = 2V, Δ’Q = 0 Þ Δ’A = 0. I начало термодинамики Þ ΔU = 0, т.е. U = const,т.к. Uид.газа = f(T) Þ T = const, Vгаза = 2V Þ p’ = p/2 Þ процесс необратим. Соберем молекулы стенкой, как поршнем Þ Δ’A (энергия механических движений окружающих тел) уменьшается на Δ’A’Þ газ при сжатии нагревается, следовательно необходимо отвести Δ’Q’ (для сохранения начальных условий) ÞΔ’A’ = Δ’Q’, т.о., когда вернем газ, расширившийся в пустоту в начальное состояние – некоторое количество энергии механических движений окружающих тел перейдет в энергию теплового движения других (или тех же самых) внешних тел, т.е. процесс необратим. Два тела Т1 и Т2, Т1 > T2 Þ некоторое Q от тела 1 к телу 2. Процесс тоже необратим. Чтобы вернуть в исходное состояние, необходимо произвести изменения в окружающей среде.

Природа необратимости – необратимым является тот процесс, обратный к которому крайне маловероятен. Т.е., чтобы определить, какие процессы могут протекать в изолированной термодинамической системе, необходимо знать вероятность различных состояний этой системы.

Характеристика – энтропия – функция состояния системы (как и Wвнутр). Система характеризуется: Δx, Δy, Δz, Δp_x, Δp_y, Δp_z – микросостояния системы p, V, T – макросостояния системы.

Система в равновесии – макропараметры постоянны, но микросостояния постоянно меняются Þ macro различными способами, каждому из которых соответствует некоторые micro.

Число различных micro – статистический вес W. Основа статистической физики – эргодическая гипотеза – все микросостояния данной термодинамической системы равновероятны. Вероятность макросостояния системы пропорциональна его статистическому весу W. моля О2 (р = 1атм, t = 20°C) Þ