9. Распределение Больцмана
Заменим в барометрической формуле M/R на m/k и p на nkT Þ nkT = n0kT exp(-mgh/kT), т.к. для изотермической атмосферы Þ n = n0 exp(-mgh/kT) – распределение молекул по высоте в изотермической атмосфере.
Т → 0, n(h) → 0, T = 0 – все молекулы на поверхности Земли. С повышением Т зависимость n от h становится более слабой и молекулы распределены по высоте почти равномерно.
Такое поведение обусловлено:
- притяжением молекул к Земле (mg);
- тепловым движением (кТ).
При конкретном распределении молекул по высоте (при каждой Т) обе тенденции уравновешивают друг друга.
mgh = Wp Þ n = n0 exp(-Wp/kT) – распределение Больцмана, n0 – плотность молекул в том месте, где εр = 0. Больцман доказал, что соотношение справедливо в случае потенциального силового поля любой природы для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.
10. Экспериментальная проверка
О. Штерн, 1920: Два цилиндра, во внутреннем -щель и нить с серебром; нить нагревается. Во внешнем цилиндре – высокий вакуум. Неподвижные цилиндры: изображение щели – резкое, вращающиеся – размытое.
v = (R - r) w/φ. По плотности напыления судят о скорости молекул.
Более точно – Ламмерт, 1929.
Пучок молекул выходит из отверстия в сосуде, стенки которого – при заданной Т и проходит через щель в 1-м диске. Через щель во 2-м – только те молекулы, которые долетели до него в тот момент, когда на их пути оказывалась щель в этом диске Þ Селектор скоростей выделяет из пучка молекулы со скоростями, лежащими в узком интервале Δv, определяемом шириной щели.
Вращается с w на φ за t = φ/w.
За это время достигнут 2 диска молекулы с
v = l/t = lw/φ – средняя скорость молекул, прошедших селектор.
Меняем w - улавливаем молекулы с другой v. Недостаток – необходимо вносить поправки, т.к. в пучке больше быстрых молекул и распределение в сосуде отличается от пучка.
11. Закон Максвелла – Больцмана
Возьмем элементарный объем dv = dx dy dz Þ dNx,y,z = n0 exp(- Wp(x,y,z)/kT)dx dy dz.
dNvx,vy,vz = NA’exp(- mv2/2 / kT)dvxdvydvz Þ Wk = Wk(vx,vy,vz) = ½ m(vx2 + vy2 + vz2) Þ
объединим оба распределения Þ
dNvx,vy,vz,x,y,z = A exp(-mv2/2 + Wp) / kT)dvxdvydvzdxdydz, где А – нормировочный множитель Þ
A = n0 (m/2pkT)3/2
В этом распределении потенциальная, кинетическая и полная энергии могут принимать непрерывный ряд значений. Если полная энергия частицы может принимать лишь дискретный ряд значений, как это имеет место, например, для внутренней энергии атома, то распределение Больцмана имеет вид
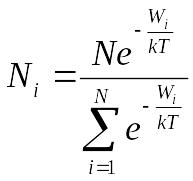
Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом или термодинамической вероятностью макросостояния.
Статистика Максвелла – Больцмана.
Распределение Максвелла и определение скорости протекания химической реакции.Даны два атома А и В. Определить скорость протекания химической реакции с образованием молекулы АВ.Для того, чтобы в смеси газов А и В образовались молекулы АВ, необходимо, чтобы атом А попал в атом В, а число таких столкновений пропорционально произведению концентраций А и В и сечению столкновений частиц. Столкновение должно быть достаточно сильным, чтобы энергия сталкивающихся частиц превышала минимальную величину, называемую энергией активации реакции.
Закон Аррениуса (1889):
Число химических превращений в единицу времени равно константе К скорости химической реакции
