7) Распределение Максвелла
Рассмотрим распределение молекул газа по скоростям. Введем воображаемое пространство скоростей (v-пространство). Скорости каждой молекулы – точка в этом пространстве. Из-за столкновений положение точек будет меняться, но их плотность в каждом месте – неизменна. Вследствие равнонаправленности всех движений – расположение точек относительно начала координат сферически симметрично. Плотность точек зависит только от модуля скорости v (или от v-2) Þ
Nf(v) Þ dNvx,vy,vz = Nf(v)dvxdvydvz Þ число молекул, компоненты скорости которых лежат в пределах
vx ¸ vx + dvx, vy ¸ vy +dvy, vz ¸ vz +dvz.
Молекулы, скорости которых заключены в интервал от v до v + dv, соответствуют точкам v-пространства, лежащим в шаровом слое толщиной dv (см. рис.)
dNv = Nf(v)4pv2dv Þ dPv = dNv/N = f(v)4pv2dv = F(v)dv.
F(v) = f(v)4pv2 – функция распределения вероятности значений v.
Функцию F(v) теоретически получил Д.К. Максвелл:
F(v) = Aexp(-mv2/2kT) · 4pv2, где m – масса молекулы, k – постоянная Больцмана, Т – термодинамическая температура; А определяется:
условие
нормировки.
Реально v ¹ ¥, но из-за экспоненциального множителя F убывает очень быстро и при больших скоростях ошибки нет.
Расчет дает для А Þ А = (m/2pkT)3/2 Þ
F(v) = (m/2pkT)3/2 exp(-mv2/2kT)4pv2 – функция распределения Максвелла. Под ехр – отношение Wк молекулы к kТ (характеризует среднее по молекулам значение этой энергии).
Наиболее вероятная скорость Þ max F(v).
Умножим и разделим полученные выражения на NA и
учтем, что kNA
= R,
mNA
= M
Þ
t = 20°C Þ <v>N2 » 470м/с, <v>O2 » 440м/с, <v>H2 » 1760 м/с.
Если смесь газов, находящихся в равновесии, то в пределах каждого – распределение Максвелла со своим значением m.
упрощается, если
ввести u
= v/vвер,
т.е.
Из расчета у 70% молекул v от Vвер не более, чем на 50%, V>Vвер в 3 раза у 0,04% молекул.
Vвер
: <v>
: Vср.кв.
=
Uвер = 1, <u> = 1,13; Uср.кв = 1,22.
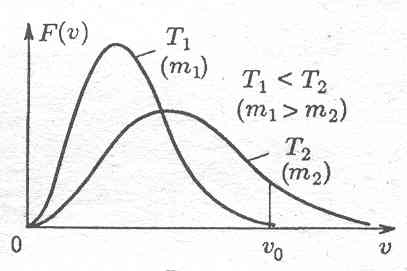
На рисунке – распределение Максвелла
для двух значение Т.
От распределения по скоростям можно
перейти к распределению молекул по
значениям кинетической энергии
поступательного движения Þ
ε = mv2/2 Þ v2 = 2ε/m,
v = (2ε/m)1/2; dv = (2mε)-1/2dε;
dNε = N·2/ (kT)-3/2exp (- ε/kT) dε Þ
f(ε) = A exp(- ε/kT) , где А = 2/ (kT)-3/2.
8.Барометрическая формула
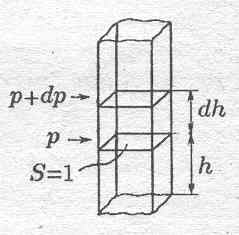
Выделим вертикальный столб с s = 1. Атмосферное давление на h обусловлено весом столба воздуха от сечения до верхней границы атмосферы Þ dh > 0 Þ dp < 0 и наоборот Þ - dp = rgdh при р ~ 1 атм. и t ~ 0° воздух хорошо подчиняется уравнению состояния идеального газа Þ
ρ=m/V = Mp/RT Þ
dp = - Mpg/RT·dh Þ
dp/p = - Mg/RT·dh
Для решения необходимо знать Т = Т(h). Для изотермической атмосферы Þ T = const Þ lnp = Cexp (-Mgh/RT) Þ h = 0 Þ C = p0 (атмосферное давление на высоте, принятой за начало отсчета) Þ p = p0exp (-Mgh/RT) – барометрическая формула.
Реально Т = Т(h), но ΔТ/Т относительно мала и формула достаточно точна. Зная р, можно определить h Þ альтиметр.