13. Метод производной по времени. Сэу с управлением по производной

Для организации поиска и поддержания экстремума СЭУ с управлением по производной предполагается, что

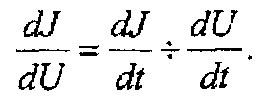
Функциональная схема системы представлена на рисунке. Здесь Д1, Д2 - дифференциаторы.

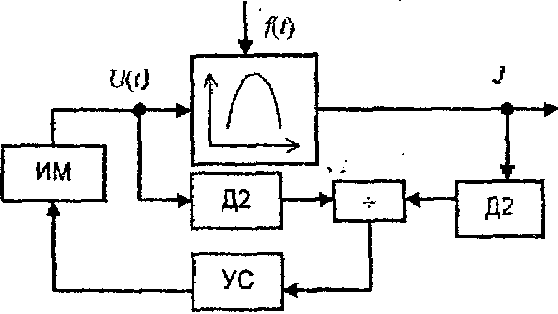
Исполнительный механизм ИМ вырабатывает управляющее воздействие U(t), которое поступает на ОУ и меняет положение рабо­чей точки таким образом, что dJ/dU стремится к нулю. Скорость движения пропорциональна dJ/dU, а направление движения опреде­ляется знаком dJ/dU.

Недостатки метода:

- в момент включения СЭУ dJ/dt и dU/dt равны нулю. Следова­тельно, существует неопределенность в операции деления в началь­ный момент времени и задача поиска экстремума становится тоже не­определенной. Поэтому в начальный момент времени необходимо подавать некоторый дополнительный сигнал dU/dt. Однако в процес­се работы также возможно случайное равенство нулю производных;

- изменение J может вызываться не только управляющим воздействием U(t), но и возмущением f, что приводит к отклонению зна­чения производной dJ/dt от ее истинного значения и, следовательно, увеличению времени поиска экстремума и дополнительным погреш­ностям его поддержания;

- наличие дифференциаторов.

Указанные недостатки ограничивают применение данной СЭУ.

Возможен другой вариант рассмотренной СЭУ, не содержащий блока деления:

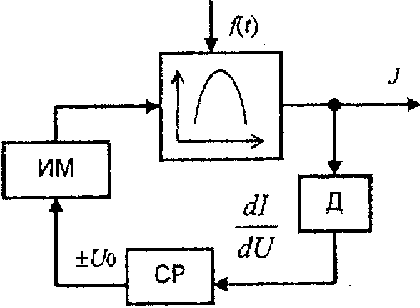
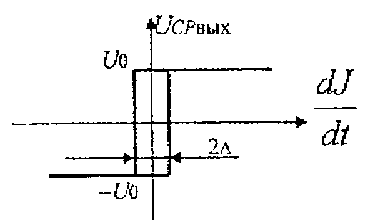
Здесь СР - сигнум-реле, выходная величина которого может прини­мать лишь дна значения - ±U₀:

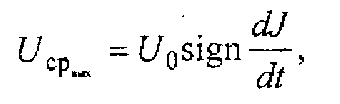
причем сигнум-реле обладает зоной нечувствительности :

Рассмотрим подробнее работу схемы. Пусть объект управления имеет экстремальную статическую характеристику (график 1 на рис.3.35). В момент включения состояние СЭУ определяется некоторыми значениями управляющего воздействия u₁ и значением управляемой величины J₁.

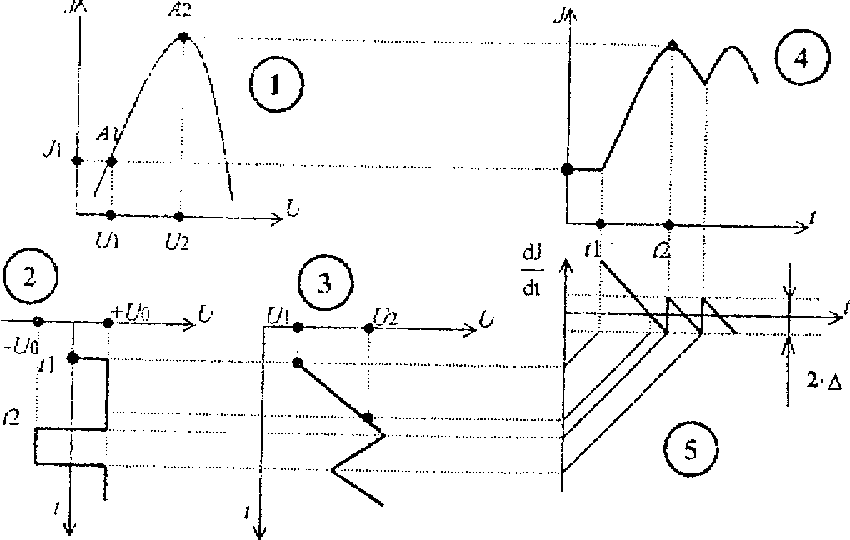
Рис. 3.35

Предположим, что в момент времени t₁ включения системы на выходе СР возникает положительный сигнал (график 2). Этот сиг­нал, поступая на исполнительный механизм (в простейшем случае интегратор), вызывает увеличение его выходной величины U (график 3).

Под влиянием U выходная величина J на выходе объекта будет изменяться, т.е. расти в соответствии со статической характеристикой объекта управления (график 4). dJ/dt (при изменении J от А1 до А2 будет уменьшаться до нуля. В момент времени t₂, когда J достигнет своего максимального значения, dJ/dt=0.

Однако в точке экстремума движение не прекратится, а за счет зоны нечувствительности изменение СР будет продолжать движение, удаляясь в противоположную сторону от экстремума. Когда dJ/dt с отрицательным знаком превысит зону нечувствительности СР (график 5), последнее сработает и изменит полярность сигнала на своем выходе (момент времени t₃). Отрицательная полярность U₀ на выходе СР вызовет реверс ИМ и, следовательно, уменьшение U, J снова ста­нет приближаться к экстремальному значению и т.д. В системе воз­никнут незатухающие колебания вокруг экстремальной точки, ампли­туда которых зависит от крутизны экстремальной статической харак­теристики вблизи точки А2, а также от величины .

Достоинством данной системы является техническая простота. К недостаткам можно отнести малое быстродействие, невысокую по­мехоустойчивость и наличие поисковых сигналов.