10. Снс с оптимизацией качества управления. Системы экстремального управления (сэу)

Задачей самонастраивающейся системы со стабилизацией каче­ства управления является достижение заданного значения показателя качества работы системы. Задачей адаптивной системы с оптимиза­цией качества является нахождение и поддержание некоторого экс­тремального значения показателя качества в условиях воздействия возмущений, причем это экстремальное значение заранее не задается и неизвестно. Такие адаптивные системы называют еще системами экстремального управления (СЭУ).

Рассмотрим следующий пример. Пусть в качестве объекта управ­ления выступает технологический процесс токарной обработки. Пока­зателем качества работы J системы управления таким объектом может служить износ режущего инструмента по задней поверхности h_oп3, а управляющим воздействием - скорость резания V.

Технологическими исследованиями установлено, что зависимость h_oп3 от V имеет экстремальный характер, причем точка экстре­мума может смещаться под действием возмущений, например при изменении твердости обрабатываемого материала НВ.

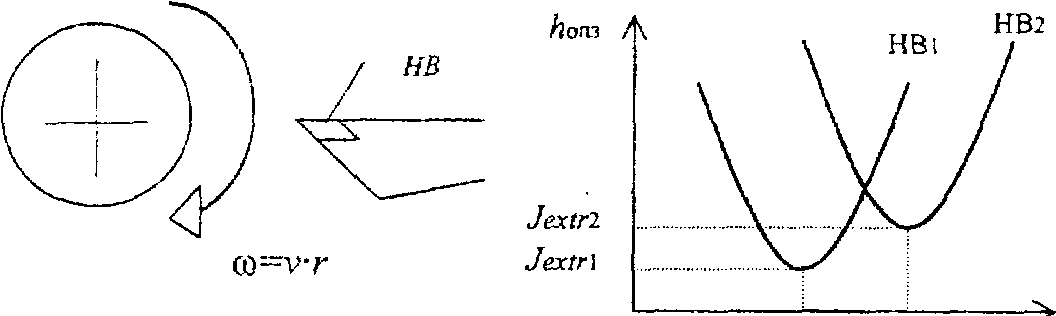
Задачей управления в данном случае будет нахождение и под­держание с заданной точностью экстремального значения J= h_oп3(V).

И в общем случае задачей СЭУ является автоматическое нахож­дение и поддержание с необходимой точностью экстремума заданно­го показателя качества J.

Отметим, что задачей обычной замкнутой САУ является сведе­ние ошибки управления ε(t) к нулю (рис. 3.14).

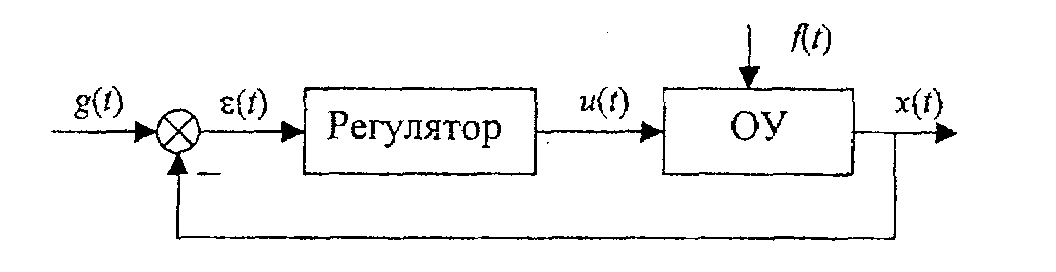
Рис. 3.14

Если:

- то такая система называется системой стабилизации;

- (известная функция времени) - системой программного управления;

- (неизвестная функция времени) - следящей системой.

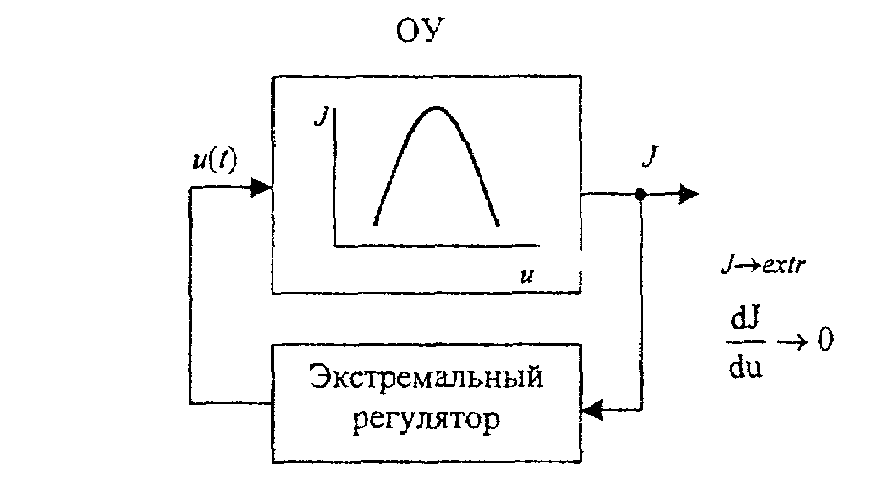
В СЭУ управление происходит иначе. ОУ СЭУ - объект с экс­тремальными характеристиками (в простейшем случае статически­ми). В качестве ошибки управления здесь выступает отклонение J от его экстремального значения (в конечной форме) или производная - (в дифференциальной форме), где u - управляющее воздействие на экстремальный ОУ.

Случаи, в которых применение СЭУ нецелесообразно:

- экстремум неподвижен на плоскости;

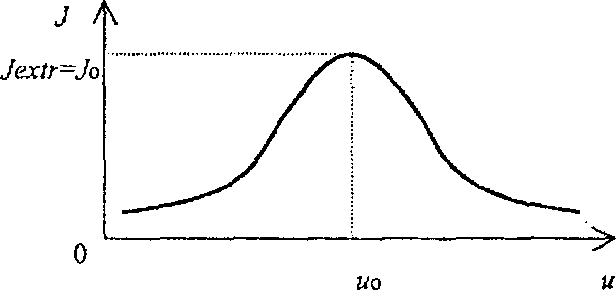
- экстремум перемещается по вертикали.

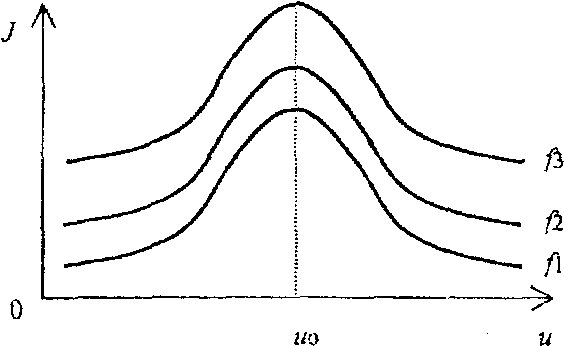
Поиск экстремума J имеет смысл только в том случае, если точ­ка (u₀, J₀) перемещается по плоскости в горизонтальном направле­нии. В противном случае задача управления может быть решена с по­мощью обыкновенной системы стабилизации (т.к. u=const).

11. Сэу с принципом управления по возмущению и по отклонению

1) СЭУ с принципом управления по возмущению

В том случае, если априори имеются данные о экстремальных статических характеристиках ОУ, то, пользуясь ими, можно заранее определить характеристику компенсации u₀=F(f).

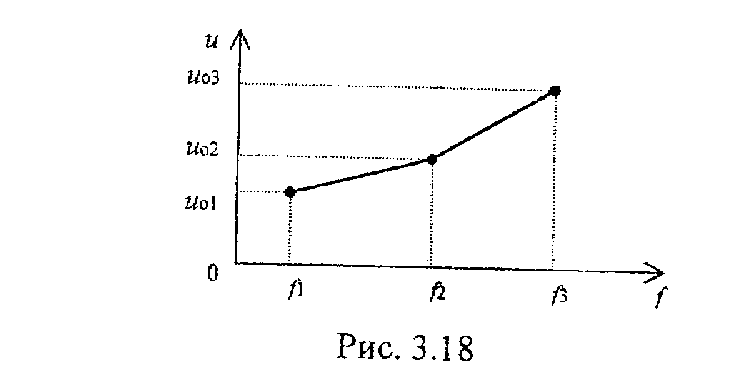
С изменением возмущений меняется управляющее воздействие u(t) в соответствии с характеристиками компенсации. В процессе управления выходная величина J объекта принимает экстремальные значения.

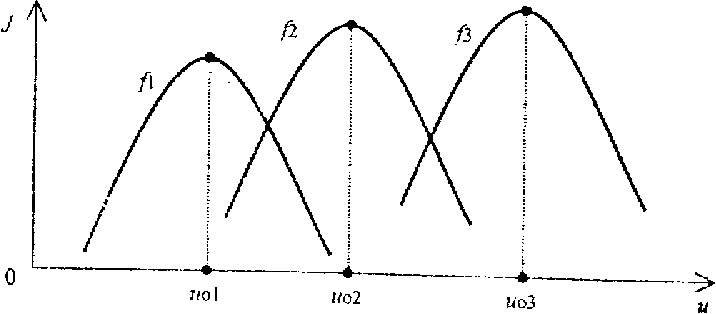
Рис. 3.19

Схема СЭУ в этом случае приведена на рис. 3.20.

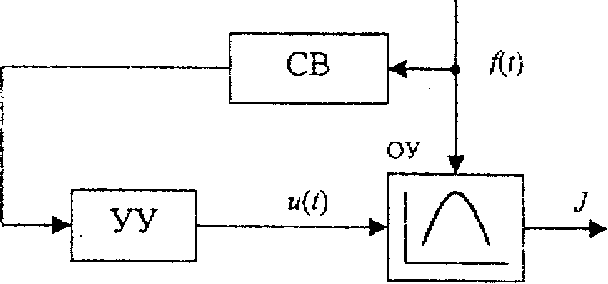
Рис. 3.20

Здесь: СВ - связь по возмущению, с помощью которой измеряется и преобразуется f(t). Система является незамкнутой, так как J непосредственно не измеряется.

К недостаткам системы можно отнести следующее:

- необходимость измерять f(t), что практически в большинстве случаев труднореализуемо;

- необходимость иметь семейство экстремальных характеристик объекта.

2) СЭУ с принципом управления по отклонению

Данные системы относятся к замкнутым системам. Для формирования управляющего воздействия используется либо отклонение J=J-J₀, либо производная dJ/du. Задача управления в такой СЭУ решается следующим образом.

В том случае, когда J является функцией одной переменной (рис 3.21), направление движения к экстремуму определяется знаком dJ/du:

- в точке А: dJ/du>0;

- в точке В: dJ/du<0;

- в точке С: dJ/du=0.

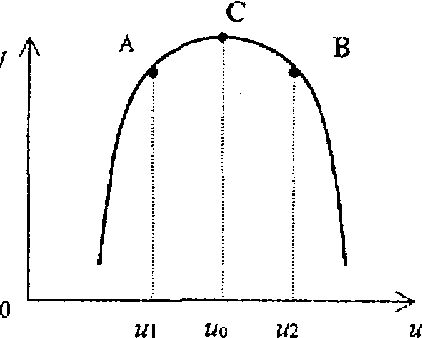
Рис. 3.21

Отсюда следует, что для движения в сторону экстремума необхо­димо:

- в точке А - увеличивать u;

- в точке В - уменьшать u;

- в точке С - u = u₀.

В общем случае, когда J является функцией нескольких перемен­ных (управляющих воздействий), J=J(u1,u2,u3), то управление движением к экстремуму будет определяться градиентом функции J. Градиент функции - это вектор, проекция которого на оси координат равны соответствующим частным производным (рис.3.22).

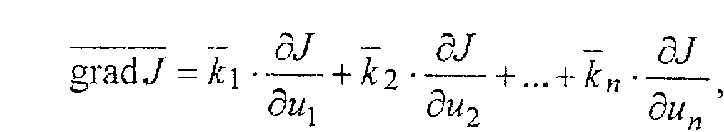
где k₁, …, k_n - единичные базисные вектора, по которым отчисляются u₁, …, u_n.

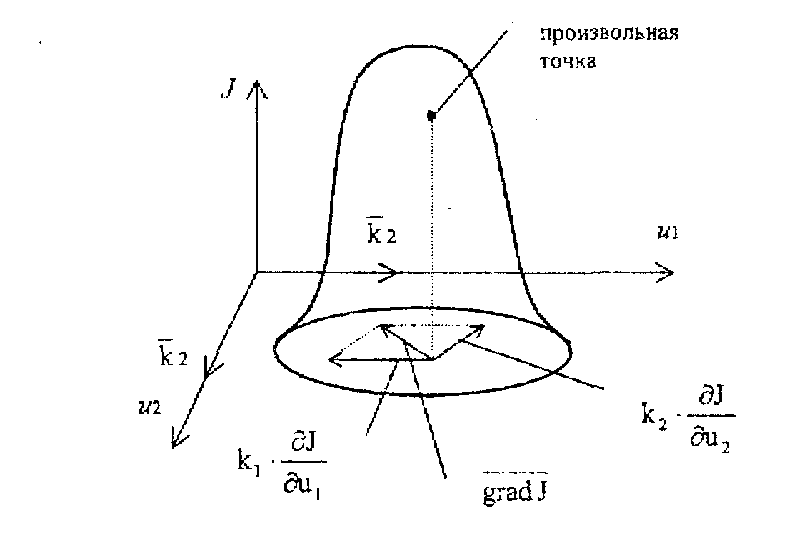
Рис. 3.22

Вектор-градиент J направлен в сторону наибольшего возрастания функции J. В точке экстремума градиент J=0. Для нахождения экс­тремума используются поисковые и беспоисковые методы.