8. Метод синтеза снс с эталонной моделью на основе прямого метода Ляпунова

Рассмотренный выше градиентный метод синтеза позволяет по­лучить структуру СНС с эталонной моделью. Однако далее необхо­димо решить традиционные задачи автоматического управления:

- обеспечить устойчивость полученной системы;

- обеспечить требуемые динамические характеристики системы.

Для исследования устойчивости динамических систем наиболее часто используется прямой метод Ляпунова. В связи с этим рассмот­рим методику применения метода Ляпунова к синтезу СНС с эталон­ной моделью. Данный подход позволяет определить структуру СНС, которая будет обладать заведомой устойчивостью.

Пусть система управления представляет собой апериодическое звено 1-го порядка, охваченное жесткой обратной связью.

Здесь

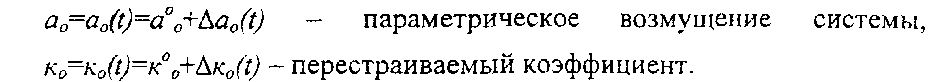
В качестве модели выберем звено, описываемое дифференциальным уравнением

Соответствующая ПФ равна

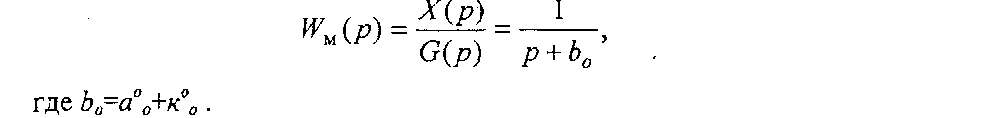
Дифференциальное уравнение, описывающее работу системы, в соответствии со структурной схемой будет иметь вид

Соответствующая ПФ:

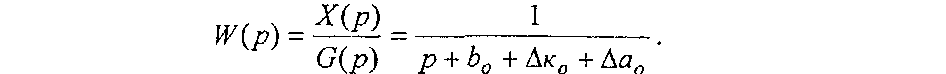
Задача контура самонастройки заключается в том, чтобы обес­печить малую ошибку рассогласования

при любом диапазоне изменения а₀(t).

На основании уравнений (3.18) и (3.19) можно записать

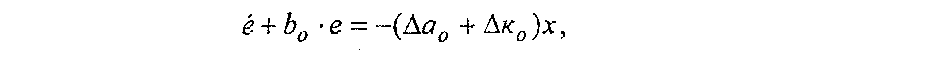
где е - координатное рассогласование движения модели и системы. По аналогии с этим величину

можно назвать параметрическим рассогласованием. Очевидно, что если у ≡ 0, то ошибка e при b₀>0 также асимптотически сходится к нулю.

Для осуществления процесса самонастройки необходимо неко­торое исполнительное устройство, перестраивающее к₀. Пусть это бу­дет интегратор и тогда к₀(р) будет изменяться по закону

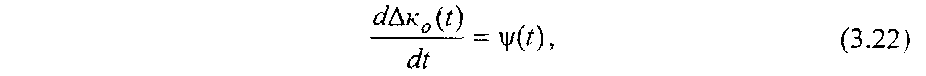
Где ψ(t) - неизвестный пока алгоритм работы контура самонастройки.

Из уравнений (3.20)-(3.22) запишем систему (3.23)

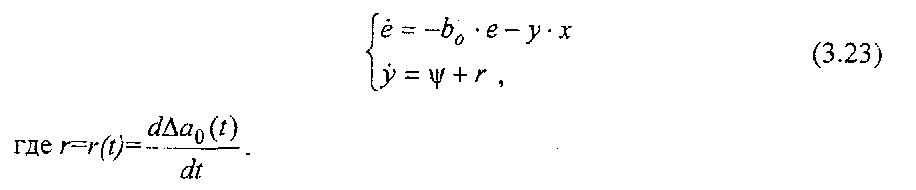
Неизвестный алгоритм работы ψ(t) можно выбрать из условия осуществления желаемого движения изображающей точки на плоско­сти {е, у}. Выполнение условия х(t)=x_м(t) при е(t)=0 сводится к тому, чтобы изображающая точка не выходила при t>t₀ из некоторой задан­ной области |е|<е₀, где е₀=соnst > 0. Данные условия полностью сов­падают с условиями устойчивости по Ляпунову.

Таким образом, если определить условия устойчивости с применением функции Ляпунова, то определится алгоритм работы кон­тура самонастройки.

Выберем функцию Ляпунова следующим образом:

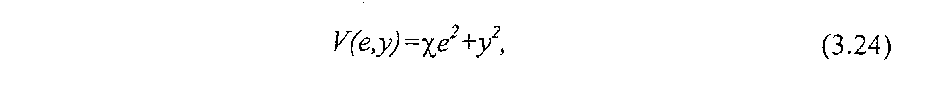
где χ - некоторый коэффициент.

Определим производную функцию Ляпунова, полагая r(t)≡0, (т.е. при t>t₀ a₀(t)=соnst)

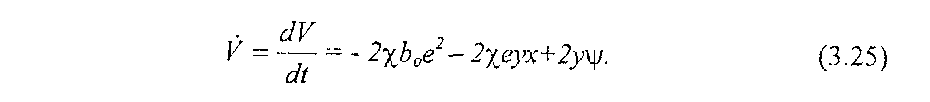
Очевидно, что если

то

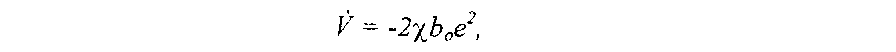
т.е. будет выполняться условие устойчивости по Ляпунову и система, работающая по алгоритму (3.26), будет асимптотически устойчива.

Структурная схема СНС, синтезированная по методу Ля­пунова, представлена на рисунке.

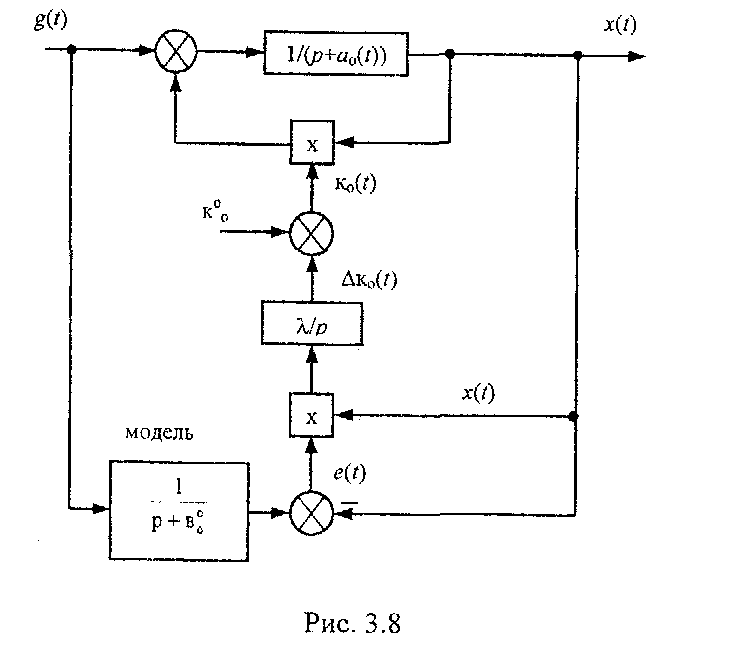
Значение коэффициента χ влияет на скорость самонастройки. При выборе функции Ляпунова другого вида изменится и алгоритм самонастройки, и структура системы. Для системы более высокого порядка процедура синтеза контуров аналогична.

9. Метод синтеза снс на основе концепции обобщенного настраиваемого объекта (оно)

Рассмотренные ранее методы синтеза СНС являются достаточно эффективными, однако при высоких порядках дифференциальных уравнений объекта они не всегда удобны. Синтез СНС с эталонной моделью в этом случае может быть существенно упрощен, если вос­пользоваться концепцией обобщенно настраиваемого объекта (ОНО).

Суть концепции ОНО заключается в следующем. Пусть имеется нестационарный объект управления (рис. 3.9). Основная часть неста­ционарного объекта управления охватывается местными параметри­ческими контурами с целью параметрической стабилизации данной нестационарной части основного контура системы.

На рисунке обозначены:

- РПУ - регулятор параметрического управления;

- УА - устройство адаптации;

- - вектор подстраиваемых коэффициентов.

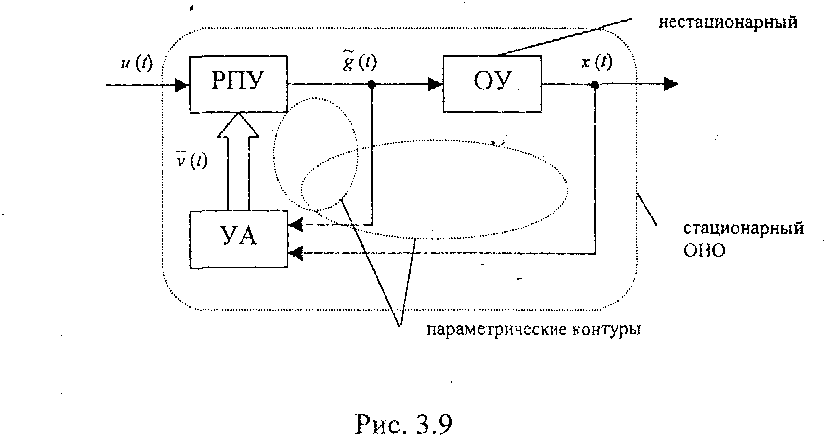
Очевидно, что параметры данных параметрических контуров должны изменяться таким образом, чтобы получаемая в результате замкнутая система описывалась стационарным ДУ. Такая система но­сит название обобщенно настраиваемого объекта - ОНО. В отличие от первоначального нестационарного ОУ, ОНО является стационарным. После этого в качестве объекта управления уже принимается ОНО и синтез регулятора основного контура может быть осуществлен с применением известных для стационарных линейных систем методов синтеза. В общем виде структура системы будет выглядеть, как пока­зано на рис. 3.10. Здесь РКУ - регулятор координатного управления.

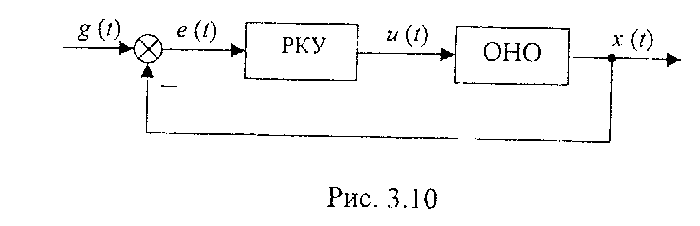
УА обеспечивает стабилизацию динамических свойств ОНО пу­тем перестройки соответствующих коэффициентов РПУ. После фор­мирования ОНО система превращается в обыкновенную стационар­ную систему.

Таким образом, введение ОНО является искусственным приемом, упрощающим процедуру синтеза СНС. Сам синтез состоит из двух этапов:

1) синтез ОНО;

2) синтез управления для ОНО.

На первом этапе необходимо определить законы перестройки вектора коэффициентов из условия, что ОНО описывается урав­нениями с постоянными коэффициентами.

Второй этап - традиционная задача синтеза стационарных систем.

Рассмотрим первый этап синтеза.

Пусть ПФ нестационарного ОУ будет

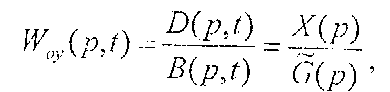
где t - признак нестационарности.

Соответствующее дифференциальное уравнение (3.27):

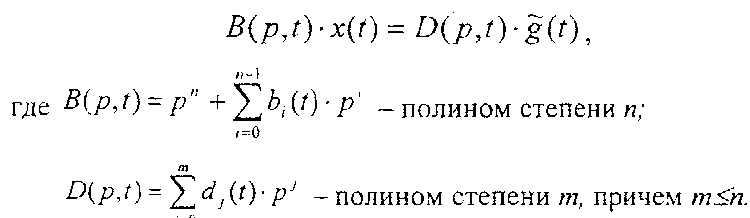
Коэффициенты полиномов определяются как

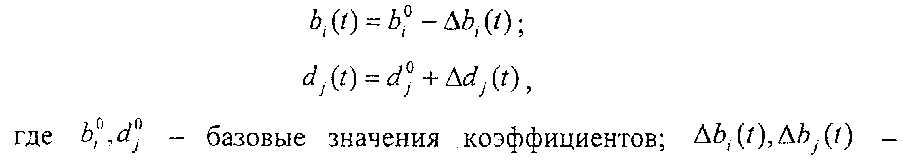
отклонения соответствующих коэффициентов от их базовых значений. Здесь знаки приращений выбраны для удобства последующих выкладок.

Тогда (3.27) можно представить следующим образом:

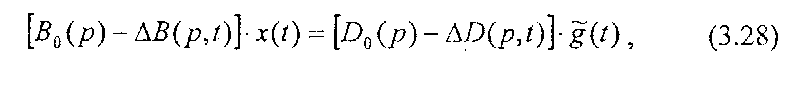
где В₀(р),D₀(р) - полиномы базовых значений; ΔВ(р,t), ΔD(р,t) - полиномы отклонений:

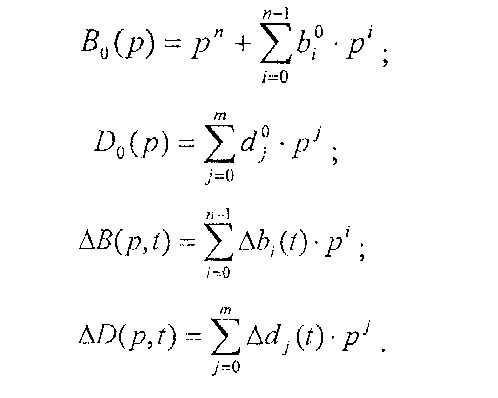
Пусть эталонная модель ОНО описывается следующей ПФ:

W_м(p)=D₀(p)/B₀(p)

или соответствующим дифференциальным уравнением

B₀(p)*x_м(p)=D₀(p)*u(t). (3.29)

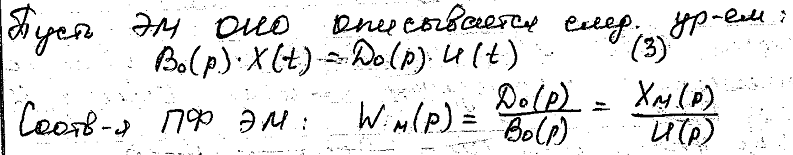
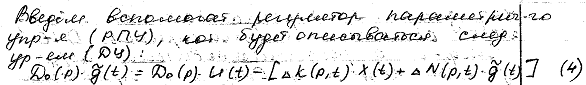
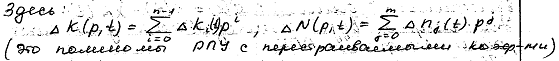
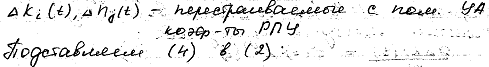
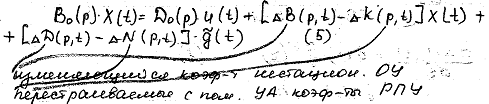
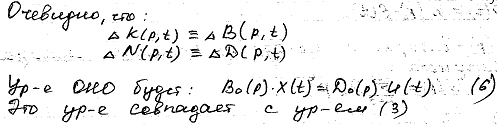
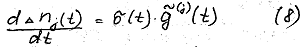
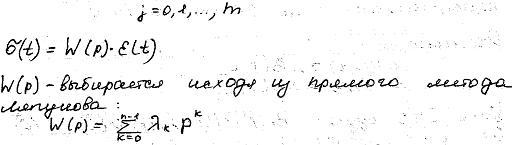
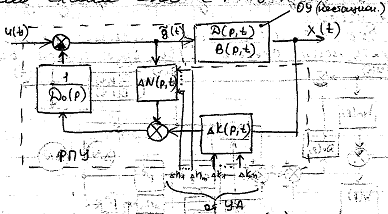
где λ_k - постоянные коэффициенты, выбираемые из условия требуе­мого знака производной функции Ляпунова. По полученным форму­лам можно составить структурную схему ОНО с устройством адапта­ции (рис. 3.12).

В случае успешного решения задачи синтеза УА следующим этапом является синтез РКУ, что является традиционной задачей син­теза обыкновенного линейного стационарного регулятора.

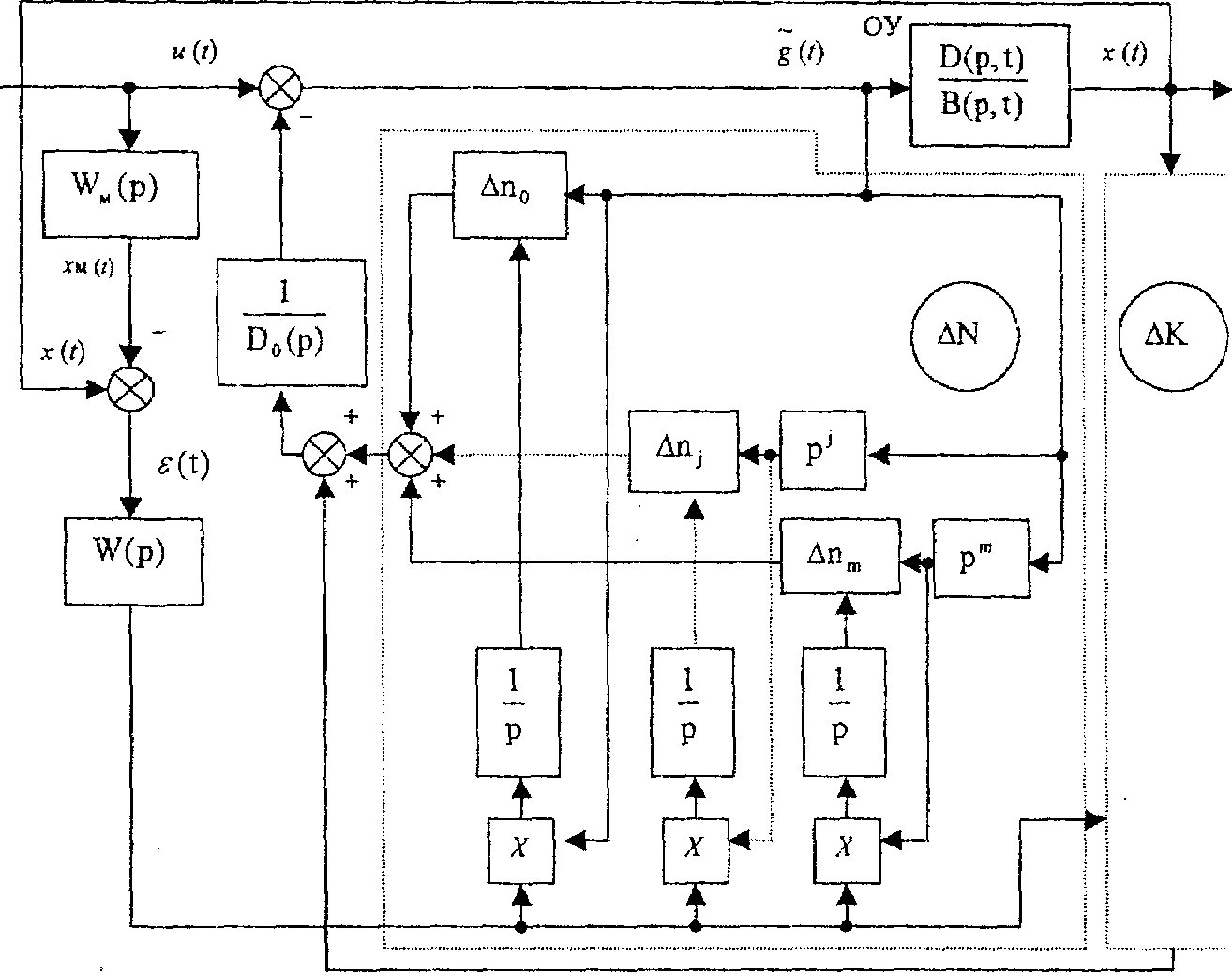
Рис. 3.12

В синтезированной схеме ОНО присутствуют такие блоки, как дифференциаторы от первого до более высоких порядков. Реализация идеального дифференцирующего блока невозможна, поэтому на практике приходится отбрасывать члены уравнений, содержащие производные высокого порядка, а производные низкого порядка определять с помощью реальных дифференцирующих устройств. Такая операция ведет к ухудшению процессов адаптации. При низких по­рядках ОУ возможно достижение хороших результатов. Для систем высокого порядка существует ряд путей, устраняющих указанные трудности.