6. Снс с моделью и большим коэффициентом усиления

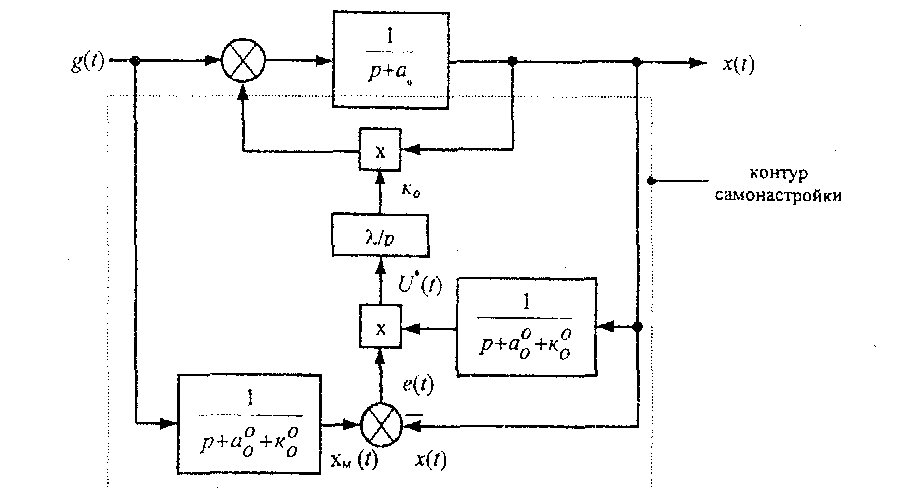
В системах управления, где возможна реализация больших ко­эффициентов усиления, возможно построение адаптивного контура без традиционной параметрической настройки регулятора основного контура. Один из вариантов структурной схемы такой системы пред­ставлен на рисунке.

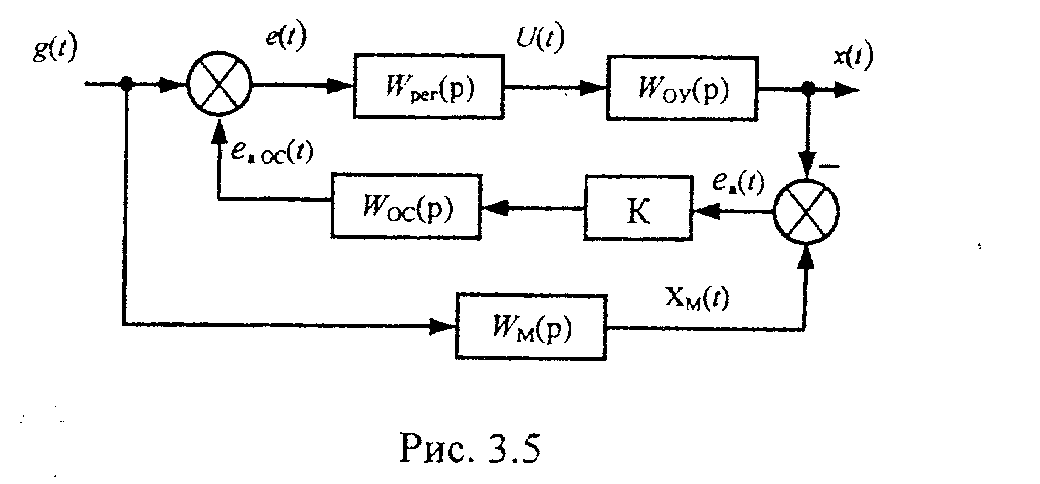
В цепь обратной связи системы вместе со звеном W_ос(р) включено звено с большим коэффициентом усиления к. Уравнения элемен­тов системы будут следующими:

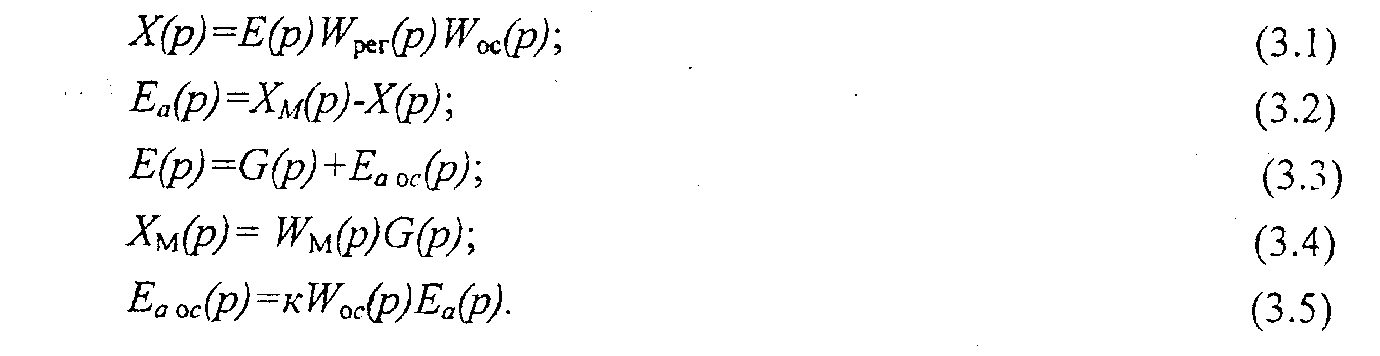
После исключения промежуточных переменных из системы уравнений (3.1) - (3.5) получаем передаточную функцию (ПФ) систе­мы по задающему воздействию

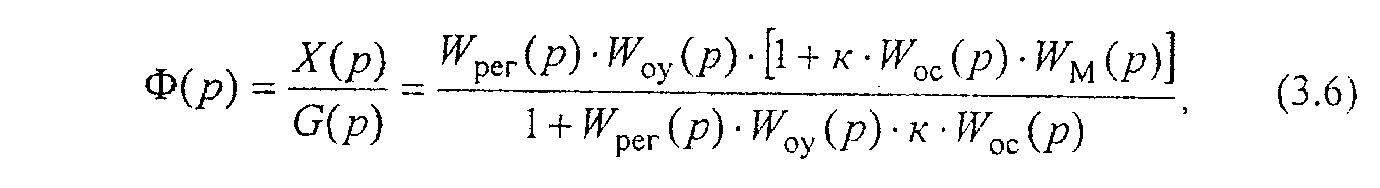
откуда после перехода в частотную область имеем

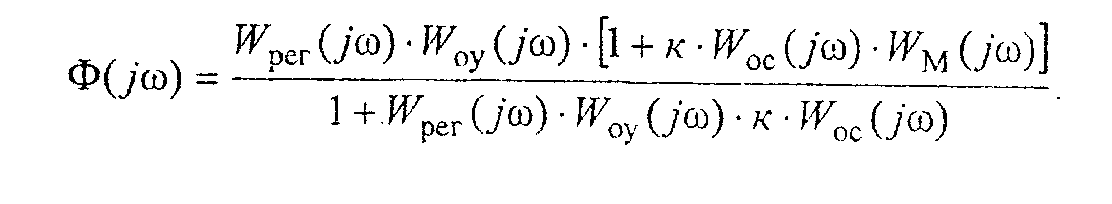
В области частот, где

выполняется приближенное равенство

и передаточная функция замкнутой системы определяется желаемой передаточной функцией модели, несмотря на возможные изменения параметров основной системы.

7. Градиентный метод синтеза снс с эталонной моделью

Рассмотрим градиентный метод синтеза на следующем примере. Пусть система управления представляет собой апериодическое звено 1-го порядка, охваченное жесткой обратной связью.

В качестве допущения примем, что в этой системе происходит достаточно медленное изменение параметрических возмущений по сравнению со скоростью протекания ее переходных процессов.

Для описания системы воспользуемся передаточной функцией, в которой переменные во времени и перестраиваемые коэффициенты входят в качестве параметров. Пусть a₀ изменяется во времени a₀= a₀(t).

Для компенсации изменения переменного во времени коэффи­циента a₀= a₀(t) cделаем перестраиваемым к₀= к₀(t).

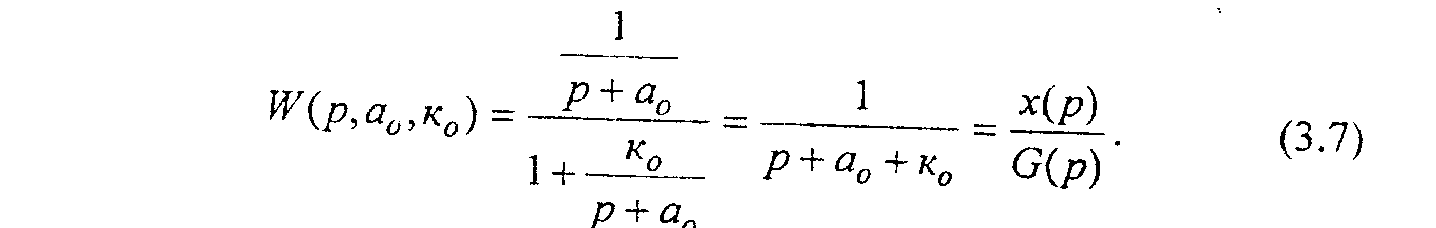
В качестве модели выберем звено следующего вида:

где а₀, к₀ - некоторые желаемые значения коэффициентов а₀, к₀;

х_м(t)- выходная координата модели.

Критерием (мерой) близости движения реальной системы и мо­дели выберем следующую функцию:

(3.9)

где e(t)=х_м(t)-х(t).

Величина J зависит от входного воздействия g(t), начального значения рассогласования, входных координат системы, а также из­меняющегося коэффициента а₀ и перестраиваемого к₀.

Сущность метода градиента состоит в организации такого алго­ритма перестройки к₀, чтобы в каждый момент времени его изменение было направлено на уменьшение критерия качества J, который явля­ется функцией от к₀. Для реализации метода необходимо знать гради­ент изменения величины J по к₀, т.е.

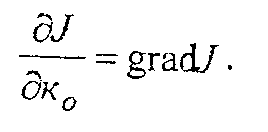
Алгоритм изменения к₀ в методе градиента строится на основе следующей формулы:

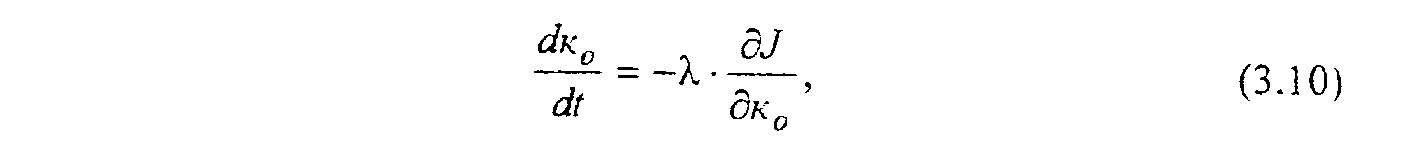
где  - коэффициент усиления контура адаптации.

Зная вид критерия качества (3.9), формулу (3.10) можно перепи­сать в следующем виде:

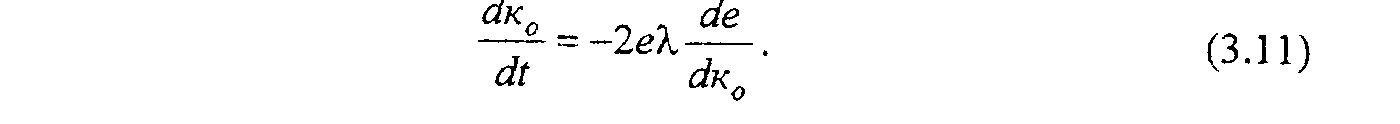
Поскольку параметры модели не зависят от времени, то

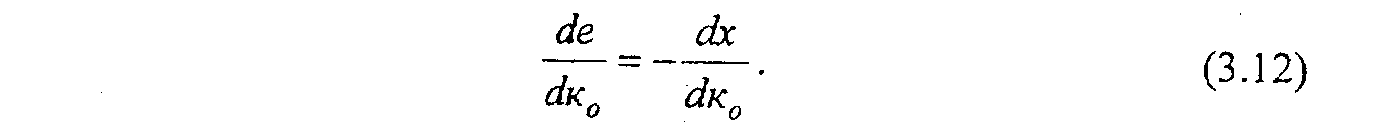
Для организации контура самонастройки по алгоритму (3.11) в каждый момент времени необходимо знать величину

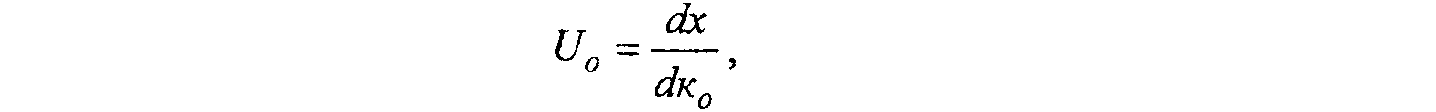
которая носит название функции чувствительности выходной вели­чины х по коэффициенту к₀. В силу коммутативности операций пре­образования Лапласа и дифференцирования по параметру будем иметь

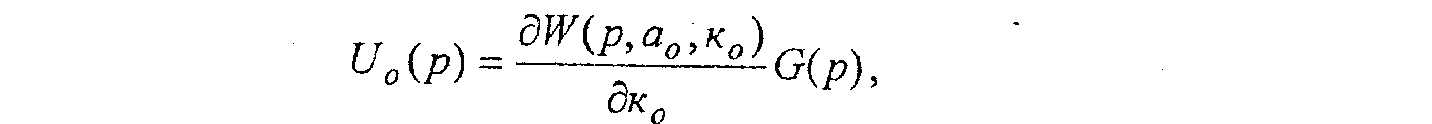
т.к.

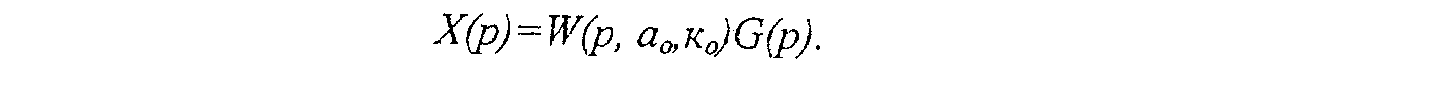
Или, по-другому:

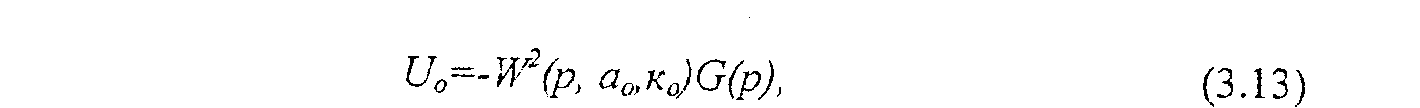
т.к.

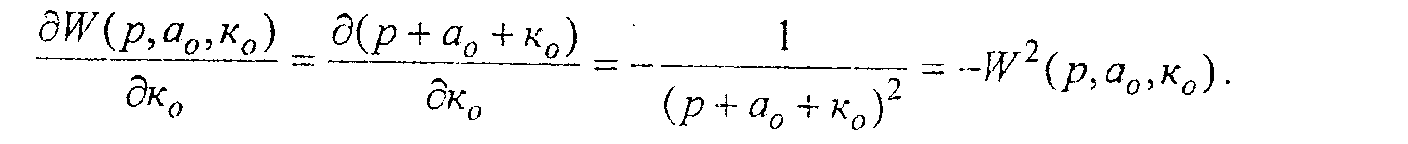
Принимая во внимание, что Х(р)=W(р, а₀ ,к₀)G(р), получим

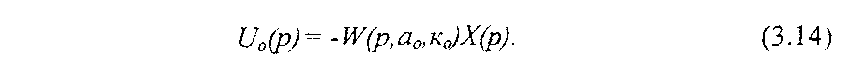
Из полученных выражений (3.13) и (3.14) можно видеть, что функция чувствительности U₀(t) зависит от времени t, перестраивае­мого коэффициента к₀ и изменяющегося а₀. Однако определение U₀(t) по полученным формулам затруднительно из-за неопределенности коэффициентов a₀ и к₀. В этом случае применяется метод «заморо­женных коэффициентов», в соответствии с которым коэффициенты a₀ и к₀ принимаются близкими к коэффициентам a⁰₀ и к⁰₀ модели. Если заранее предположить, что эта задача успешно выполняется, то ПФ реальной системы W(р, а₀, к₀) можно заменить на ПФ модели W_м(р, а⁰₀, к⁰₀). Таким образом можно получить некоторую приближенную функцию чувствительности

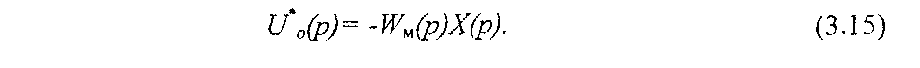
Подставим далее (3.12) и (3.15) в (3.11):

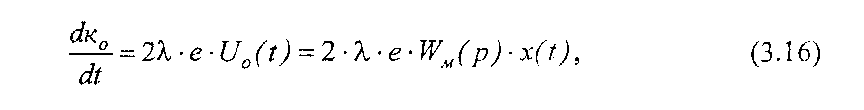
откуда получим

к₀=(2/p) E(p)W(p)X(p) (3.17).

Полученная формула (3.17) позволяет определить значения пе­рестраиваемого коэффициента к₀ в зависимости от значения выход­ной координаты, ошибки управления и ПФ модели.

Структурная схема СНС с эталонной моделью, синтезированная по методу градиента, представлена на рисунке.