3.2 Нахождение допустимого диапазона изменения компонент вектора ограничений

Ресурс 1. В оптимальной симплекс таблице переменная является базисной, поэтому ресурс 1- недефицитный. Для недефицитных ресурсов диапазон устойчивости решения (учитывая, что у нас неравенство вида « »):

Ресурс 2. Переменная является небазисной, поэтому ресурс 2 - дефицитный. Так, как второе ограничение вида « », то по следующей формуле найдём диапазон изменения коэффициента :

,

3.3 Нахождение нового решения при изменении уровней запасов ресурсов

а) суммарное количество статуэток должно быть не меньше 2;

.

Новые значения базисных переменных определим по формуле: .

Из оптимальной симплекс таблицы извлекаем .

С учетом нового значения новое значение вектора ограничений: . Тогда

,

Получив значения и , подсчитаем новое значение целевой функции: .

б) суточный запас металла увеличен до 70 кг.

.

Так как первый ресурс недефицитный, то его изменение повлияет только на значение соответствующей остаточной переменной:

; значение ЦФ не изменится:

в) суммарное количество вил и совков должно быть не меньше 45;

Поскольку, , в данном случае базис оптимального решения изменится (для нахождения нового решения нужно либо решать задачу заново, либо, изменив данные, применить двойственный симплекс-метод и продолжить вычисления).

3.4 Нахождение допустимого диапазона изменения коэффициентов целевой функции

Имеем задачу на минимум.

Переменная является базисной, диапазон изменения коэффициентов целевой функции находится по формуле:

,

Переменная является небазисной, поэтому диапазон устойчивости:

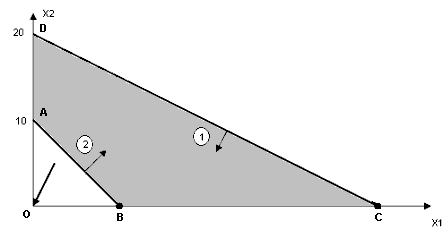
Решение задачи графическим способом (Проверим полученные ранее результаты)

;

1-й ресурс 2-й ресурс

Множество допус­тимых решений задачи – многоугольник . Оптимумом является точка В(10;0). .

Ресурс 1. Как мы уже определили, ресурс 1 – недефицитный, поэтому его ценность .

Интервалы изменения правой части:

• увеличивать её можно не ограниченно – на оптимум это не повлияет:

• уменьшать правую часть можно до тех пор, пока прямая (1) не пройдёт через точку оптимума B (10; 0).: ,

,

• т.о. (что и требовалось доказать).

Ресурс 2.

Найдём интервалы изменения правой части.

• Для улучшения значения ЦФ уровень запаса 2-го ресурса нужно уменьшать, предельный сдвиг – до точки О(0;0): , соответствующее значение ЦФ: .

Изменение значения ЦФ и уровня запаса:

,

.

• При увеличении уровня запаса 2-го ресурса значение ЦФ также увеличивается, предельный сдвиг – до точки С(40; 0). Найдем соответствующие изменения значений ЦФ и правой части: ;

;

;

.

• Т.о. (что и требовалось доказать).

• Теперь получим ценность ресурса: .