2.2. Функции спроса на ресурсы и функции издержек.
Фирма «Металлургический комбинат»
Найдем функции спроса на ресурсы и функцию издержек фирмы А, если потребление ресурсов не ограничено (долгосрочный период). Для этого воспользуемся следующими формулам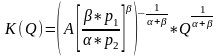и:
и
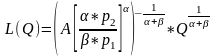
Они представляют собой функции спроса на ресурсы и позволяют для известного значения объема выпуска Q определить необходимые количества ресурсов.
Подставим значения K(Q) и L(Q) в выражение функции издержек:
и получим зависимость суммы затрат от объема выпуска в следующем виде:
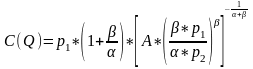
Подставим исходные данные в формулы выше и найдем функции спроса на ресурсы и функцию издержек.
-
Фирма Металлургический комбинат
Год
x1(Q)
x2(Q)
C(Q)
1
818,359
492,272
72153,856
2
996,334
599,331
87845,724
3
1128,165
678,632
99469,157
4
1239,588
745,657
109293,215
5
1339,388
805,690
118092,454
Таблица 19. Расчет функций спроса на ресурсы и издержек для фирмы «Металлургический комбинат»
По полученным значениям построим графики данных функций:
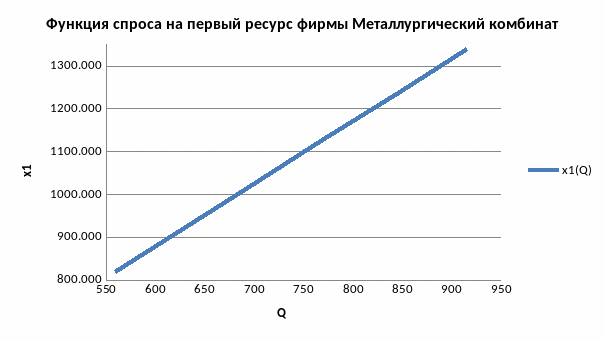
Рисунок 20. Функция спроса на ресурс К для фирмы «Металлургический комбинат»
Рисунок 21. Функция спроса на ресурс L для фирмы «Металлургический комбинат»
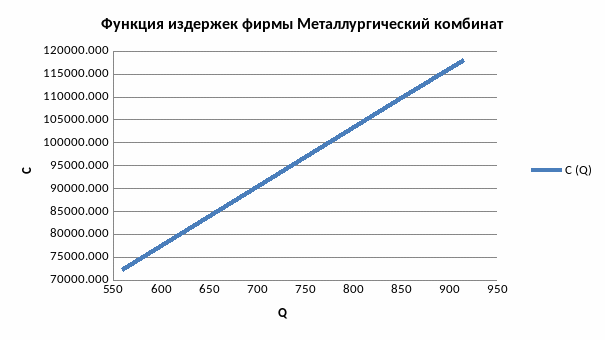
Рисунок 22. Функция издержек для фирмы «Металлургический комбинат»
Проанализировав полученные графики, приходим к выводу, что с увеличением объема производства увеличивается спрос на каждый из ресурсов и при этом, соответственно, увеличиваются издержки фирмы.
Фирма «Металл-комплект»
Найдем функции спроса на ресурсы и функцию издержек фирмы «Металл-комплект». Учитывая, что оптимальной стратегией фирмы «Металл-комплект» является использование только первого ресурса, получим следующие функции спроса на ресурсы для фирмы «Металл-комплект»:
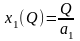и
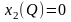
Они позволяют для известного значения объема выпуска Q определить необходимые количества ресурсов.
Подставим значения х1(Q) и х2(Q) в выражение функции издержек и получим зависимость суммы затрат от объема выпуска в следующем виде:
Данное уравнение представляет собой функцию издержек для фирмы «Металл-комплект».
Составим таблицу для построения функций спроса на ресурсы и функции издержек.
-
Фирма Металл-комплект
Год
x1(Q)
x2(Q)
C(Q)
1
1126,286
0,000
212128,354
2
1263,655
0,000
238000,833
3
1373,824
0,000
258750,377
4
1471,993
0,000
277239,804
5
1562,162
0,000
294222,485
Таблица 20. Расчет функций спроса на ресурсы и издержек для фирмы «Металл-комплект»
По полученным значениям построим графики данных функций:
Рисунок 23. Функция спроса на ресурс х1 для фирмы «Металл-комплект»
Рисунок 24. Функция издержек для фирмы «Металл-комплект»