1.3. Получение выражений экономико-математических характеристик для производственных функций фирм ооо «Металлургический комбинат» и оао «Металл-комплект».
Для производственных функций фирм ООО «Металлургический комбинат» и ОАО «Металл-комплект» получим выражения экономико-математических характеристик: среднего и предельного продуктов, коэффициентов эластичности по ресурсам, предельной нормы замены ресурсов. Изобразим графически зависимости экономико-математических характеристик как функций соответствующего ресурса.
Для фирмы ООО «Металлургический комбинат»:
Найдем для производственной функции фирмы А выражения средних продуктов. Средние продукты характеризуют удельный эффект использования ресурсов в производственном процессе фирмы.
В нашем случае, средними продуктами являются:
1. Средняя фондоотдача – это отношение объема произведенного продукта к стоимости основных фондов:
2. Средняя производительность труда – это отношение произведенного продукта к количеству затраченного труда:
Подставляя в данные формулы производственную функцию, соответствующую фирме А, и, производя необходимые вычисления, получим:
-
Металлургический комбинат
AQx1=
1*x1-0,75*x20,75
AQx2=
1*x10,25*x2-0,25
Найдя выражения средних продуктов, рассчитаем их значения от каждого ресурса, фиксируя при этом второй ресурс на его значении в 1 году. Полученные данные представлены в таблице ниже.
-
Средние продукты для фирмы Металлургический комбинат
Год
AQk
AQl
1
0,699
1,127
2
0,426
1,330
3
0,321
1,460
4
0,265
1,557
5
0,229
1,635
Таблица 8.Расчёт средних продуктов для фирмы «Металлургический комбинат»
Кроме этого найдем для производственной функции фирмы А выражения предельных продуктов. Предельные продукты характеризуют эффект в виде прироста объема продукции, получаемый от увеличения затрат ресурсов.
В нашем случае это:
1. Предельная фондоотдача - характеризует величину дополнительного эффекта от каждой затраченной единицы капитала при данном сочетании ресурсов (K, L):
2. Предельная производительность труда – характеризует величину дополнительного эффекта от каждой затраченной единицы труда при данном сочетании ресурсов (К,L):
Подставляя в данные формулы производственную функцию, соответствующую фирме А, и, производя необходимые вычисления, получим:
-
Предельные продукты для фирмы Металлургический комбинат
MQx1=
0,25*1*x1-0,75*x20,75
MQx2=
0,75*1*x10,25*x2-0,25
-
Предельные продукты для фирмы Металлургический комбинат
Год
MQk
MQl
1
0,174
0,846
2
0,106
0,998
3
0,080
1,096
4
0,066
1,169
5
0,057
1,227
На основе полученных данных построим графики зависимости средних продуктов от затраченных ресурсов. Сравним средние и предельные продукты от каждого ресурса.
Рисунок 7. Средняя и предельная фондоотдача для фирмы «Металлургический комбинат»
Рисунок 8. Средняя и предельная производительность труда для фирмы «Металлургический комбинат»
Проанализировав графики средних и предельных продуктов, делаем вывод, что предельные продукты убывают предельно ниже средних. Также в фирме «Металлургический комбинат» предельный продукт меньше среднего продукта, т.е. с увеличением затрат ресурса значение предельного и среднего продуктов падает.
Найдем коэффициенты эластичности по ресурсам для фирмы А.
Коэффициенты эластичности производственных ресурсов выражают процентный прирост продукта от одно процентного прироста одного из ресурсов.
Эластичность продукта по фондам определяется по формуле:
Эластичность продукта по труду:
Подставляя в данные формулы выражения средних и предельных продуктов, , получим:
и
Зависимость коэффициентов эластичности от соответствующих затраченных ресурсов представлена в таблице ниже.
-
Коэффициенты эластичности для фирмы Металлургический комбинат
Год
Ex1
Ex2
1
0,250
0,751
2
0,250
0,751
3
0,250
0,751
4
0,250
0,751
5
0,250
0,751
Таблица 9. Расчёт коэффициентов эластичности для фирмы «Металлургический комбинат»
На основе полученных данных построим графики зависимости коэффициентов эластичности от затраченных ресурсов.
Рисунок 10. Эластичность по капиталу и труду для фирмы «Металлургический комбинат»
На основе полученных данных можно сделать вывод, что коэффициенты эластичности для фирмы А равны соответствующим показателям α и β независимо от затраченных ресурсов, а значит являются стабильными показателями производственной функции.
Найдем для производственной функции фирмы А выражения предельных норм замены. Предельной нормой замены одного ресурса другим называется величина, показывающая, каков объем высвобождаемого ресурса при увеличении затрат ресурса-заменителя на единицу. Вычисляется по формуле:
и
Подставляя в данные формулы выражения предельных продуктов, получим:
Найдя выражения предельных норм замены, рассчитаем их значения от каждого ресурса-заменителя, фиксируя при этом заменяемый ресурс на его значении в 1 году. Полученные данные представлены в таблице ниже (Таблица )
-
Предельная норма замены фирмы "Металлургический комбинат"
Год
Skl
Slk
1
4,851
0,206
2
9,399
0,106
3
13,671
0,073
4
17,692
0,057
5
21,483
0,047
Таблица 10. Расчёт предельных норм замены для фирмы «Металлургический комбинат»
На основе полученных данных построим график эффекта замены:
Рисунок 11. График предельной нормы замены KL для фирмы «Металлургический комбинат»
На основе полученных данных делаем вывод о том, что эффект замены увеличивается с увеличением ресурса заменителя.
Для фирмы ОАО «Металл-комплект»:
Найдем для производственной функции фирмы А выражения средних продуктов.
Средние продукты характеризуют удельный эффект использования ресурсов в производственном процессе фирмы и вычисляются по формулам:
и
, соответственно
подставляя в данные формулы производственную функцию, соответствующую фирме В, и , производя необходимые вычисления, получим:
-
Металл-комплект
AQx1=
(2,01*х1+3,99*х2)/х1
AQx2=
(2,01*х1+3,99*х2)/х2
Найдя выражения средних продуктов, рассчитаем их значения от каждого ресурса, фиксируя при этом второй ресурс на его значении в 1 году. Полученные данные представлены в таблице ниже.
-
Средние продукты для фирмы Металл-комплект
Год
AQx1
AQx2
1
5,115
6,566
2
4,771
6,887
3
4,642
7,029
4
4,584
7,097
5
4,564
7,120
Таблица 11. Расчёт средних продуктов для фирмы «Металл-комплект»
Также найдем для производственной функции фирмы В выражения предельных продуктов.
Предельные продукты характеризуют эффект в виде прироста объема продукции, получаемый от увеличения затрат ресурсов.
Найдя выражения предельных продуктов, запишем их зависимость от каждого ресурса. Полученные данные представлены в таблице ниже.
-
Предельные продукты для фирмы Металл-комплект
Год
MQx1
MQx2
1
2,01
3,99
2
2,01
3,99
3
2,01
3,99
4
2,01
3,99
5
2,01
3,99
Таблица 12. Расчёт предельных продуктов для фирмы «Металл-комплект»
На основе полученных данных построим графики зависимости средних и предельных продуктов от затраченных ресурсов:
Рисунок 12. Средний и предельный продукты по х1 для фирмы «Металл-комплект»
Рисунок 13. Средний и предельный продукты по х2 для фирмы «Металл-комплект»
Таким образом, на основе полученных данных делаем вывод, что в фирме «Металл-комплект» предельный продукт меньше среднего продукта и постоянен, причем средний продукт приближается к предельному продукту.
Найдем коэффициенты эластичности по ресурсам для фирмы В. Коэффициенты эластичности производственных ресурсов выражают процентный прирост продукта от одно процентного прироста одного из ресурсов и вычисляются по формулам:
и
Подставляя в данные формулы выражения средних и предельных продуктов, получим:
и
Найдя выражения средних продуктов, рассчитаем их значения от каждого ресурса, фиксируя при этом второй ресурс на его значении в 1 году. Полученные данные представлены в таблице ниже.
-
Коэффициенты эластичности для фирмы Металл-комплект
Год
Ex1
Ex2
1
0,392
0,608
2
0,420
0,580
3
0,432
0,568
4
0,438
0,562
5
0,439
0,561
Таблица 13. Расчет коэффициентов эластичности для фирмы «Металл-комплект»
На основе полученных данных построим графики зависимости коэффициентов эластичности от затраченных ресурсов:
Рисунок 14. Эластичность по х1 и х2 для фирмы «Металл-комплект»
Найдем для производственной функции фирмы В выражения предельных норм замены. Предельной нормой замены одного ресурса другим называется величина, показывающая, каков объем высвобождаемого ресурса при увеличении затрат ресурса-заменителя на единицу. Вычисляется по формуле:
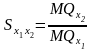и
Подставляя в данные формулы выражения предельных продуктов, получим:
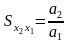
Найдя выражения предельных норм замены, выразим их зависимость от затраченных ресурсов. Полученные данные представлены в таблице ниже.
-
Предельная норма замены фирмы "Металл-комплект"
Год
Sx1x2
Sx2x1
1
0,502
1,990
2
0,502
1,990
3
0,502
1,990
4
0,502
1,990
5
0,502
1,990
Таблица 14. Расчет предельных норм замены для фирмы «Металл-комплект»
На основе полученных данных построим графики эффекта замены:
Рисунок 15. Предельная норма замены х1х2 для фирмы «Металл-комплект»
Таким образом, на основе полученных данных делаем вывод о том, что предельная норма замены постоянная и не зависит от затраченных ресурсов и равна отношению коэффициентов заменяемого ресурса к ресурсу-заменителю. Это означает, что ресурсы полностью взаимозаменяемы.