
VI.2. Операции над матрицами
39. (Норма
матрицы.) Вычислить норму
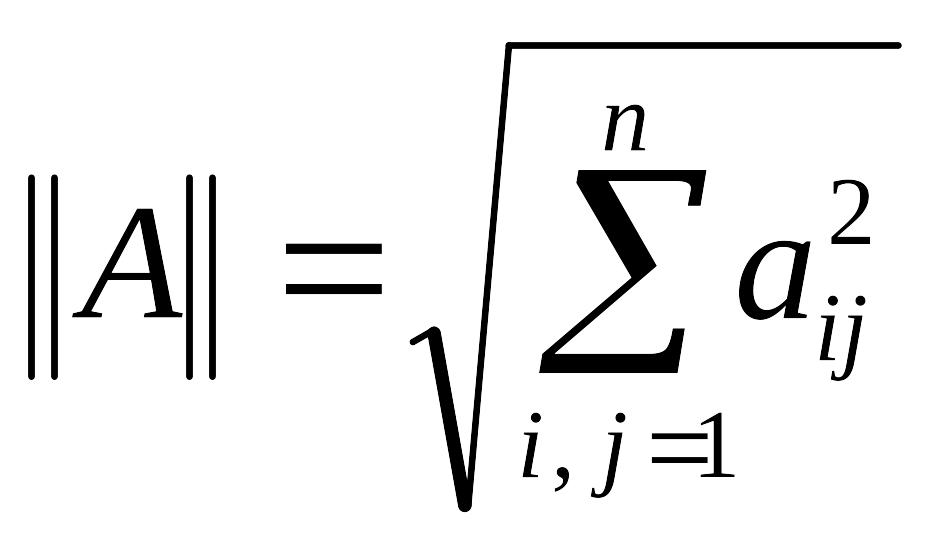 квадратной матрицы A=(aij)
n‑го порядка.
квадратной матрицы A=(aij)
n‑го порядка.
40. (Построение матриц.) Построить матрицы
а)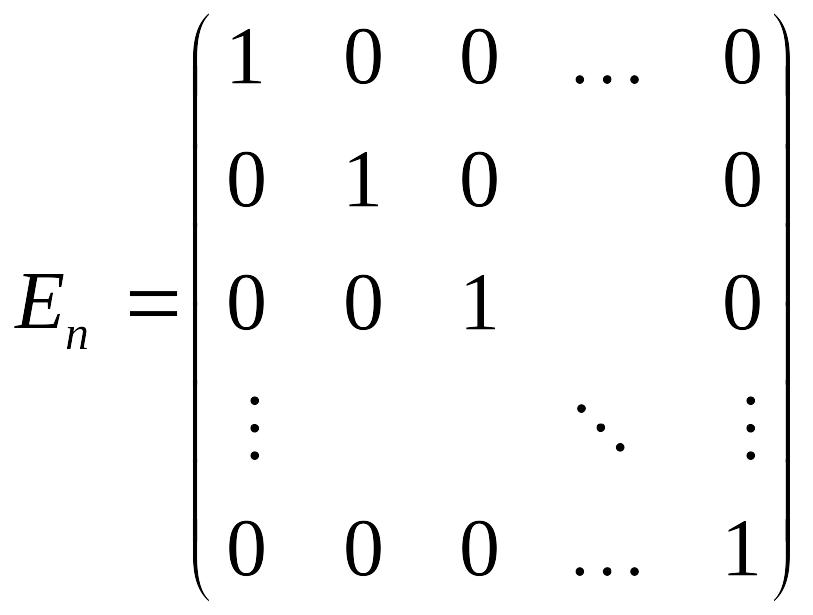 б)
б)

в)  г)
г) 
д)

41. (Построение
матриц.) Построить матрицы C=(![]() ),
),
![]() ,
с элементами
,
с элементами
 ;
;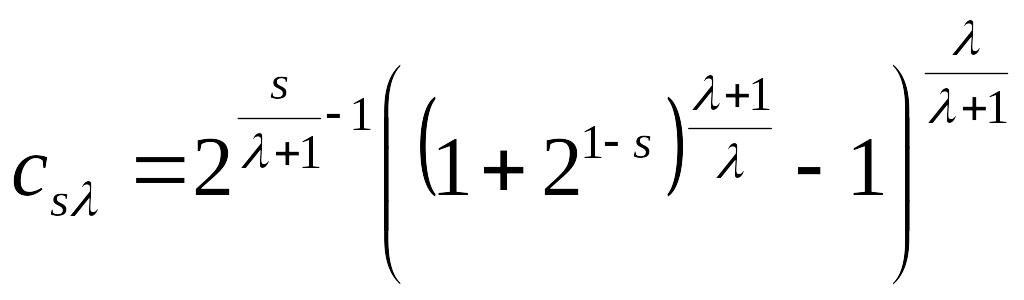 .
.
42. (Циркулянты.)
По заданному вектору
![]() построить циркулянтную (n
построить циркулянтную (n![]() n)-матрицу
A, у которой первая
строка совпадает с a,
а каждая последующая строка есть
циклический сдвиг (влево) предыдущей
строки.
n)-матрицу
A, у которой первая
строка совпадает с a,
а каждая последующая строка есть
циклический сдвиг (влево) предыдущей
строки.
43. (Вертикальная
рекурентность, или матрицы, образованные
числами Стирлинга snk
и Snk
первого и второго рода.) Построить
(m
m)-матрицы
s=(snk)
и S=(Snk),
![]() ,
,
![]() ,
где snk=Snk=0
при n<k
и
,
где snk=Snk=0
при n<k
и
s00=S00=1; sn0=Sn0=0 для n>0;
sn+1,k=sn,k–1–nsnk,
Sn+1,k=Sn,k–1+kSnk
для n+1![]() k
1.
k
1.
44. (Построение некоторых известных матриц.)
Для заданного вещественного вектора (x1,…,xn) построить (n n)-матрицу Вандермонда W=(wij), где
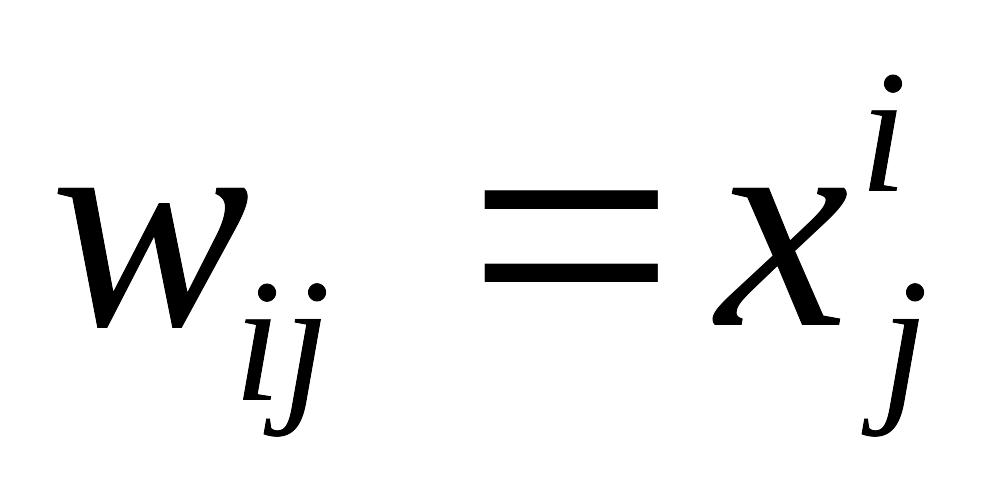 ,
i, j=1,2,…,n.
,
i, j=1,2,…,n.Для заданных вещественных векторов (x1,…,xn) и (y1,…,yn) построить (n n)-матрицу Коши C=(cij), где cij=(xi+yj)–1, i, j=1,2,…,n.
Построить целочисленную (n n)-матрицу Смита S=(sij), где sij=н.о.д.(i,j), i, j=1,2,…,n.
Вычислить определители матриц W, C и S.
Указание: известно, что
![]() ;
;
![]() ;
;
![]() ,
,
где det A
– определитель матрицы A,
![]() – функция Эйлера, определяемая как
число целых чисел из отрезка [1,k],
взаимно простых с k.
– функция Эйлера, определяемая как
число целых чисел из отрезка [1,k],
взаимно простых с k.
45. (Транспонирование матрицы.) Транспонировать заданную квадратную матрицу.
46. (Числа разбиений.) Построить целочисленную квадратную матрицу Q=(qij) порядка s, элементы которой определены следующим образом:
q1k=qk1=1 для всех k=1,2,…; qmm=qm,m–1+1 для всех m=2,3,…;
qmk=qmm при m<k; qmk=qm,k–1+qm–k,k при m>k.
Замечание. qmk есть число способов представления натурального m в виде суммы неупорядоченных натуральных слагаемых, каждое их которых не превосходит r. Например, q5,4=7, так как 5 = 4+1 = 3+2 = 3+1+1 = 2+2+1 = 2+1+1+1 = 1+1+1+1+1.
47. ("Упаковка" и "распаковка" трехдиагональных матриц.)
Преобразовать матрицу
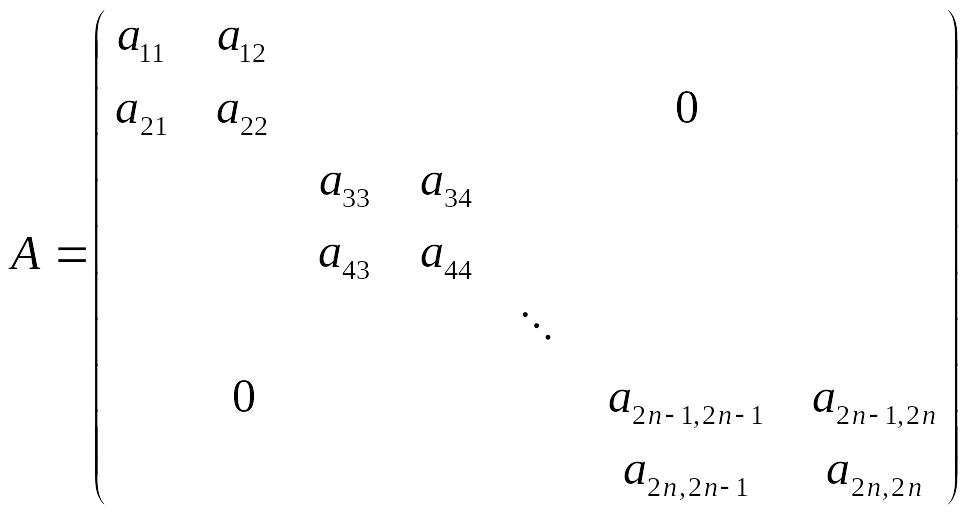
в вектор
![]() .
.
Выполнить обратное преобразование.
Преобразовать матрицу

в вектор
![]() .
.
Выполнить обратное преобразование.
48. ("Упаковка" и "распаковка" треугольных матриц.)
Преобразовать треугольную матрицу

в вектор
![]() .
.
Выполнить обратное преобразование.
49. ("Упаковка" и "распаковка" симметричной матрицы.)
По заданной симметричной (n n)-матрице A=(aij) построить вектор
![]() .
.
Выполнить обратное преобразование.
50. (Трехдиагональные, треугольные и симметричные матрицы.) Установить, является ли заданная матрица: а) трехдиагональной, б) треугольной, в) симметричной.
51. (Решение системы линейных уравнений.)
Найти решение системы линейных уравнений
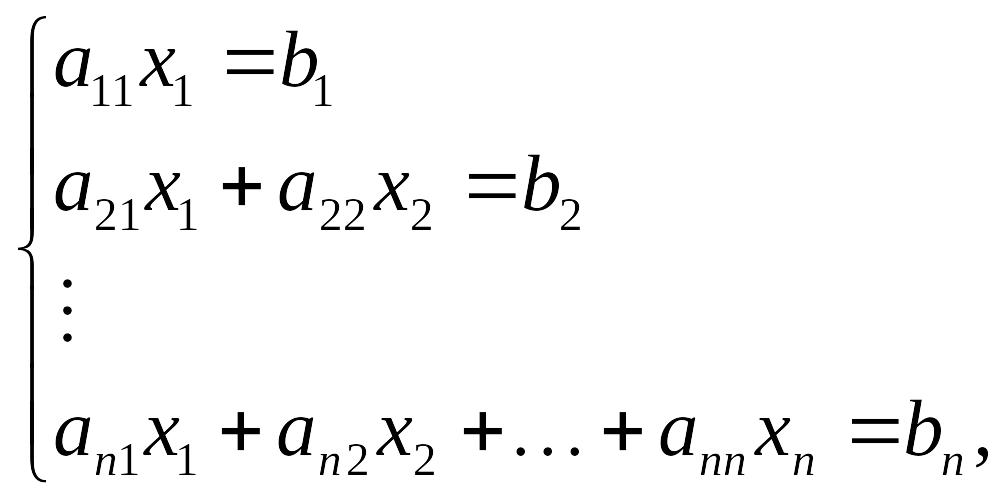
где
![]() ,
i=1,2,…,n.
,
i=1,2,…,n.
Найти решение системы линейных уравнений
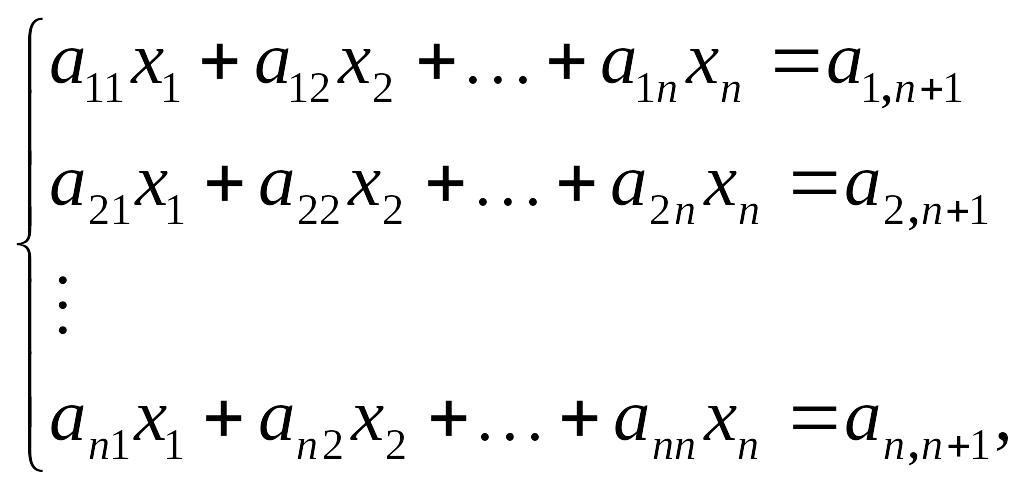
используя метод Гаусса – метод последовательного исключения неизвестных.
Строки
Скопированную строку выведите на экран дисплея с разрядкой (с пробелами) между символами.
Произведите копирование одной строки в другую при их задании через клавиатуру.
Введите с клавиатуры две строки, различающиеся одним символом. Напишите программу по определению индексов двух различных символов для введенных строк. Длину строк возьмите не менее 7 символов.
Произведите копирование одной строки в другую без применения функции strcpy().
С клавиатуры введите свою фамилию (буквами латинского алфавита), выведите ее на консоль в прямом и обратном порядке, например, Ivanov, vonavI.
Напишите программу преобразования десятичной системы счисления в двоичную. Исходное десятичное число считайте целым без знака.
Программный код решения примера:
#include <stdio.h>
#include <conio.h>
#include <iostream>
using namespace std;
int main (void) {
const char D[] = {
'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
int newNumber[80];
long int inputNumber;
int i = 0, base = 2;
cout<<"\n\t Enter a positive integer: ";
cin>>inputNumber;
// Прямой процесс преобразования десятичного числа в двоичное
Do
{
newNumber[i] = inputNumber % base;
++i;
inputNumber /= base;
} while ( inputNumber != 0 );
//Запись преобразованного числа в обратном порядке
cout<<"\n\t Result after conversion: ";
for (--i; i >= 0; --i)
cout<<newNumber[i];
cout<<"\n\n Press any key: ";
_getch();
return 0;
}
Подсчитайте число итераций цикла для преобразования числа 13 в двоичное число.
Вместо цикла do–while примените цикл while.
Напишите программу преобразования двоичного числа в десятичное число. Проверьте работу программы с помощью инженерного калькулятора.
Проверьте программу для преобразования десятичных чисел в числа с основанием 3 и 8.
Примените посимвольный ввод строк и произведите их конкатенацию с выводом на дисплей результата конкатенации.
Произведите конкатенацию имени и фамилии пользователя с помощью операторов цикла, т.е. без помощи функции strcat(). Предусмотрите пробел между именем и фамилией.
Присоедините к своему имени свою фамилию, записанную в обратном порядке.
Напишите программу по выводу на консоль информации о человеке с помощью пароля, который вводится с клавиатуры. Информация должна содержать имя, фамилию, год, месяц и число рождения, место рождения. В качестве пароля возьмите свою фамилию с учетом регистра (т.е. прописные или строчные буквы).
Примените функцию tolower() для перевода в строчные буквы.
В символьной строке находятся слова и два числа, разделенные пробелами или запятыми. Выделите из строки слова и числа, разместите их в отдельных массивах. При этом считанные числа и слова разместите в дополнительных символьных массивах. Выведите значения сформированных символьных массивов. Произведите преобразование строковых (символьных) чисел к числам с плавающей точкой (тип double ). Если после десятичной точки находится нуль (или нули), то число определите как целое, в противном случае – как число с плавающей точкой, т.е. типа double.
Для решения примера используем библиотечные функции isalpfa() для определения буквы во входном потоке (с подключением библиотеки ctype.h ), isspace() – для определения пробелов во входном потоке (с подключением библиотеки ctype.h ), isdigit() – для определения цифры во входном потоке (с подключением библиотеки ctype.h ), atof() – для преобразования строки чисел в число с плавающей точкой (с подключением библиотеки stdlib.h ), atoi() – для преобразования строки чисел в целое число (с подключением библиотеки stdlib.h ), modf() – для выделения целой и дробной части числа (с подключением библиотеки math.h ), strlen() – для определения длины строки (с подключением библиотеки string.h ).
Программный код решения примера:
#include <stdio.h>
#include <conio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
#include <math.h>
#include <iostream>
using namespace std;
#define N 79
int main (void) {
double r = 0.0, b3, b4;
int i, j, k, m, n, A[N], n2, n3, n4;
char str[N], str2[N], str3[N], str4[N];
// Множественная инициализация
i = j = k = m = 0;
// Обнуление символьных массивов
for (n2 = 0; n2 < N; ++n2)
str2[n2] = 0;
for (n3 = 0; n3 < N; ++n3)
str3[n3] = 0;
for (n4 = 0; n4 < N; ++n4)
str4[n4] = 0;
cout<<"\n\t Print line with 2-nd numbers:\n\t ";
cin.getline(str, sizeof(str)/sizeof(str[0]));
while (str[i] != '\0') {
if ( isalpha(str[i]) || isspace(str[i]) )
str2[j++] = str[i];
else if (isdigit(str[i]) || str[i] == '.')
A[k++] = i; // массив индексов цифр потока
else
str2[j++] = str[i];
++i; }
cout<<"\n\t A string of words and symbols:\n\t"; puts(str2);
if (k > 0)
{
n = 0;
for (i = 0; i < k; ++i){
if (A[i + 1] - A[i] == 1 )
str3[n++] = str[A[i]];
else if (A[i+1] - A[i] > 1)
{m = A[i+1]; str3[n++] = str[A[i]]; break;}
}
}
cout<<"\n";
if (n > 0) {
r = modf(atof(str3), &b3);
if (!r) // если не нуль
cout<<"\t The number is an integer: "<< atoi(str3);
else
cout<<"\t The number is real (double): \n"<< atof(str3);
}
if (m > 0 ) {
j = 0;
for (i = m; i <= A[k - 1]; ++i)
str4[j++] = str[i];
r = modf(atof(str4), &b4);
if (!r) // если не нуль
cout<<"\t The number is an integer: "<<atoi(str4);
else
cout<<"\t The number is real (double):\n"<<atof(str4));
}
cout<<"\n\n Press any key: ";
_getch();
return 0;
}
В программе функция modf() возвращает величину дробной части числа (переменная r ) и целой части (от переменных b3, b4 взяты их адреса, т.е. &b3, &b4 ). Анализ массива с индексами цифр исходного символьного массива дает возможность выделить индексацию двух чисел входного потока. Функция gets_s() автоматически добавляет символ конца строки '\0', поэтому при объявлении размерности символьного массива следует предусмотреть одно место для '\0'. Для переносимости программ размерность массива в функции gets_s() определена с помощью функции sizeof().
