1. 2. Упражнения для самостоятельной работы
1. Найти область определения следующих функций
а)
Ответ:
Единичный круг с центром в начале
координат, при этом также входит единичная
окружность
.
б)
Ответ: Полуплоскость, расположенная
над прямой
2. Найти частные производные функций
а)
Ответ:
б)
Ответ:
в)
Ответ:
.
г)
Ответ:
д)
Ответ:
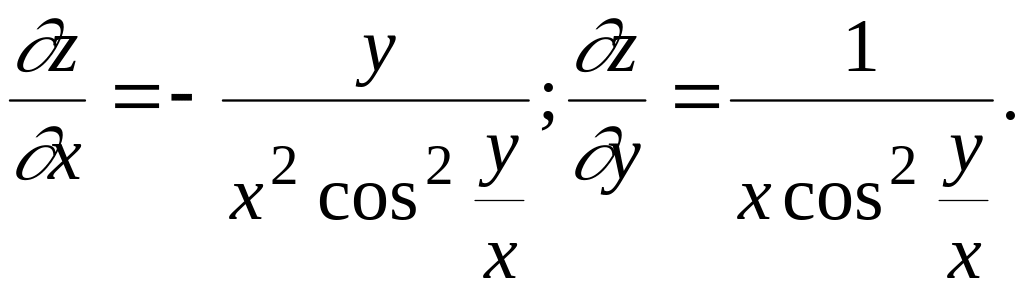
3. Проверить, удовлетворяет ли функция
уравнению
4. Найти полные дифференциалы функций
5. Вычислить приближенно
6.
7.Найти
Ответ: 0 .
8.
Найти
Ответ:
Ответ:
10. Найти dz , если x y z = x + y + z ;
Ответ:
11.
В точке М(1,0,-1)
найти уравнение касательной плоскости
и нормали к поверхности
Ответ:
12.
Найти
Ответ: 0.
13.
Найти
Ответ:
14.
Найти
Ответ:
15.
Найти grad z
в точке М(2,1),
если
Ответ:
16. Найти grad U в точке М(1,2,3), если U = x y z;
Ответ:
17.
Найти производную функции
в точке М(1,1)
в направлении биссектрисы первого
координатного угла.
Ответ:
18. Исследовать на максимум и минимум функции:
а)
в точке М(1,0).
б)
в точке М(4,-2).
19.
Найти наибольшее и наименьшее значения
функции
в круге
Ответ:
Наибольшее значение Z=1
на границе круга в точках
20.
Найти наибольшее и наименьшее значения
функции
в треугольнике, ограниченном прямыми
x
= 0, y
= 0, x
+ y
= 3.
Ответ:
Наименьшее значение Z
= -19 на границе в точке
,
наибольшее значение z
= -1 на границе в точке
1.3. Задачи для контрольной работы
Тема: “ Дифференциальное исчисление функции многих переменных “
Задача 1. Найти область определения функции и изобразить ее геометрически.
;
Задача 2
2.1. Дана функция . Показать, что
2.
2. Дана функция
Показать,
что
2.
3.
Дана функция
Показать, что
2.
4. Дана функция
Показать,
что
2. 5. Дана функция Показать, что
2.6.
Дана функция
Показать, что
2.7.
Дана функция
Показать,
что
2.
8. Дана функция
Показать, что
2.
9. Дана функция
Показать, что
2.10.
Дана функция
Показать, что
