5. Рассмотрим практические упражнения.

1. Дискретная случайная величина Х дана таблицей распределения вероятностей

Х	2	3	6
P	0,3	0,6	0,1

Вычислить числовые характеристики М (Х), D (X), , V(X).

Находим математическое ожидание

.

Дисперсию вычислим по формуле

.

Составим закон распределения для случайной величины

	4	9	36
P	0,3	0,6	0,1

Вычислим .

Итак,

D(X) = 10,2 - .

Находим среднее квадратическое отклонение

.

Определим коэффициент вариации

%.

2. Две независимые дискретные случайные величины даны таблицами распределения вероятностей

X	2
P	0,6	0,4

Y
P	0,6	0,3	0,1

Определить: М (2X + 3Y), D (X + 2), D (3X + 2Y), M (2XY).

Составить таблицу распределения вероятностей для случайной величины X + Y.

При вычислении числовых характеристик воспользуемся их свойствами. Для этого предварительно вычислим M(X), D(X), M(Y), D(Y).

Имеем

; ;

На основании свойств линейности математического ожидания имеем

М (2X + 3Y) = 2M (X) +3M(Y) = ; Далее на основании свойства 4 дисперсии имеем D (X + 2) = D(X) = 0,24;

C учетом свойств дисперсии 4 и 5 получим

D (3X + 2Y) = 9D(X) + 4D(Y) = 12,6.

На основании свойства 4 математического ожидания имеем

Теперь составим закон распределения случайной величины X+Y.

Возможные значения случайной величины X+Y равны всевозможным суммам случайной величины Х со случайной величиной Y, то есть:

,

.

Находим вероятности возможных значений. В частности, . Так как случайные величины X, Y независимые, поэтому события в свою очередь являются независимыми. По теореме умножения вероятностей независимых событий имеем

.

Итак,

Аналогично,

;

;

;

;

;

Теперь составим таблицу распределения вероятностей для случайной величины X+Y

X+Y	3	4	5	6	7	8
P	0,36	0,24	0,18	0,12	0,06	0,04

Замечание. В качестве самоконтроля следует проверить сумму элементов второй строки, то есть, равна ли единице. В самом деле, имеем

0,36 + 0,24 + 0,18 + 0,12 + 0,06 + 0,04 = 1.

3. Дана плотность распределения непрерывной случайной величины X

.

Найти: Функцию распределения F(x); математическое ожидание; дисперсию; среднее квадратическое отклонение; коэффициент вариации; P(1 < X < 6); Построить графики функций f (x), F (x).

Пользуясь формулой , найдем интегральную функцию распределения F(x). Будем искать по промежуткам для любого имеем

Если , то

При >2, имеем

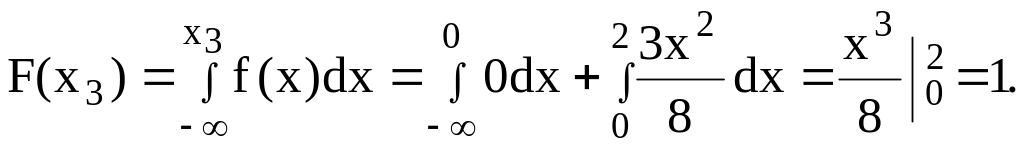
Итак, функция распределения

.

Находим математическое ожидание

.

Определим дисперсию по формуле

. Итак,

Находим .

Определим коэффициент вариации

%.

Вычислим P (1 < X < 6) при помощи интегральной функции

.

Если же дана плотность распределения, то можно найти следующим образом

.