Срс №3 вариант №19

Задание 1.

Имеются следующие данные об остатках вкладов в Сбербанке РФ за 1999 – 2005 гг., млрд. руб.:

Год	1999	2000	2001	2002	2003	2004	2005
Остатки вкладов, млн. руб.	106,4	111,0	114,3	117,2	119,1	120,0	121,8

Для анализа динамики остатков вкладов рассчитайте за 1999-2005 гг. следующие показатели:

1) средний уровень ряда;

2) абсолютные приросты (цепные, базисные, средние);

3) темпы роста и прироста (цепные, базисные, средние);

4) абсолютное значение одного процента прироста (по годам, среднее).

Сделайте выводы.

Решение:

Для расчета требуемых показателей воспользуемся следующими формулами.

1) Средний уровень ряда(моментного) рассчитывается по формуле:

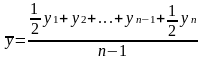
2) Абсолютные приросты (цепные, базисные, средние) рассчитываются по формуле:

- цепной абсолютный прирост ( ) – это разность между сравниваемым уровнем и уровнем, который ему предшествует: .

- базисный абсолютный прирост ( ) исчисляется как разность между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения: .

- для определения среднего абсолютного прироста ( ) сумма цепных абсолютных приростов делится на их число:

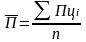или

3) Темпы роста и прироста (цепные, базисные, средние) рассчитываются по формуле:

- цепной темп роста:

- базисный темп роста:

- для определения среднего темпа роста ( ) применяется формула средней геометрической , где Тр₁, Тр₂ и т. д. - индивидуальные цепные коэффициенты роста.

Средний темп роста можно определить и по абсолютным уровням ряда динамики: .

- цепной темп прироста:

- базисный темп прироста:

- средний темп прироста (если вычислен в процентах), (если вычислен в виде коэффициента).

4) Абсолютное значение одного процента прироста (по годам, среднее) рассчитывается по формуле:

.

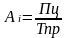Рассчитаем указанные выше показатели, результаты расчетов сведем в таблицу:

Год	1999	2000	2001	2002	2003	2004	2005
Остатки вкладов, млн. руб.	106,4	111	114,3	117,2	119,1	120	121,8
Средний уровень ряда, млн. руб.	115,95
Абсолютный прирост(базисный), млн. руб.	х	4,6	7,9	10,8	12,7	13,6	15,4
Абсолютный прирост(цепной), млн. руб.	х	4,6	3,3	2,9	1,9	0,9	1,8
Абсолютный прирост(средний), млн. руб.	2,44
Темп роста(базисный), %	х	104,32%	107,42%	110,15%	111,94%	112,78%	114,47%
Темп роста(цепной), %	х	104,32%	102,97%	102,54%	101,62%	100,76%	101,50%
Темп роста(средний), %	102,74%
Темп прироста(базисный), %	х	4,32%	7,42%	10,15%	11,94%	12,78%	14,47%
Темп прироста(цепной), %	х	4,32%	2,97%	2,54%	1,62%	0,76%	1,50%
Темп прироста(средний), %	2,74%
Абсолютное значение одного процента прироста, млн. руб.	х	1,06	1,11	1,14	1,17	1,19	1,20
Абсолютное значение одного процента прироста (среднее), млн. руб.	1,15

Выводы:

Для наглядности выводов построим диаграммы:

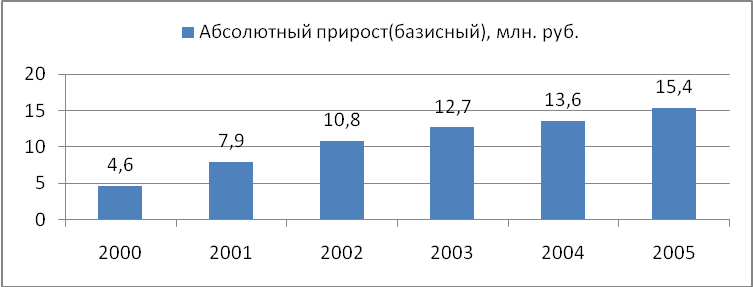
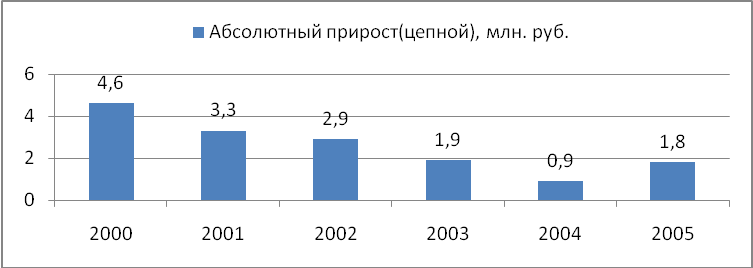
По сравнению с 1999г. наблюдается рост абсолютной величины остатков вкладов, однако анализ цепных абсолютных приростов показывает снижение с каждым годом абсолютного прироста. Средний абсолютный прирост составил 2,44 млн. руб.

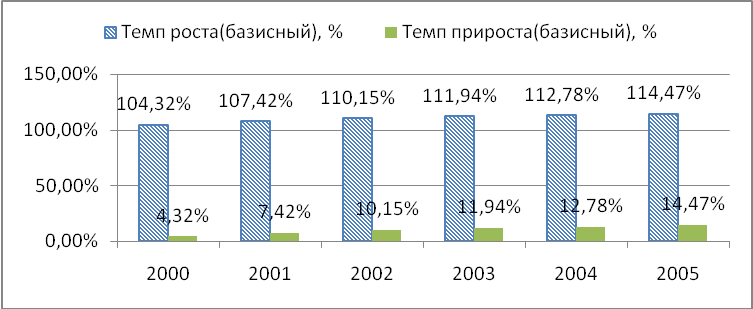
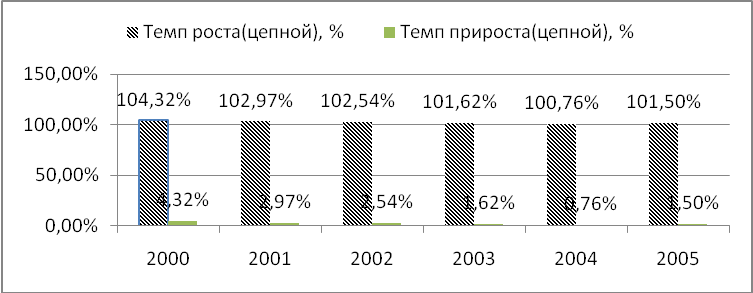
Динамика темпов роста (прироста) подтверждает вывод по абсолютным показателям. Остатки вкладов растут, но темпы роста с каждым готом замедляются. Средний тем роста составил 102,74% (прироста 2,74%).

Задание 2.

Имеются данные о связи между средней взвешенной ценой и объемом продаж облигаций на ММВБ 01.01.2004 г.:

Номер серии	A	B	C	D	E	F	G	H	I	J
Средняя взвешенная цена, тыс. руб.	84,42	82,46	80,13	63,42	76,17	75,13	74,84	73,03	73,41	71,34
Объем продаж, млрд. руб.	79,5	279,7	71,4	242,8	76,3	74,7	210,7	75,1	75,5	335,3

Необходимо:

1) выбрать факторный и результативный признаки;

2) обосновать вид уравнения регрессии;

3) рассчитать параметры регрессии;

4) дать графическое изображение теоретической зависимости;

5) проанализировать параметры уравнения регрессии;

6) дать оценку тесноты связи между признаками;

7) дать оценку значимости связи между признаками.

Сделайте выводы.