2. Доверительные границы|граница| для средних и относительных величин

определяют формулами:

P_ген=P_выб t _*m_{p ,} где:

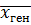• и P_ген - значение средних и относительных величин, рассчитанных для генеральной совокупности;

• и P_выб – значение средних и относительных величин, рассчитанных для выборочной совокупности;

• m_x и m_p – средние ошибки соответствующих показателей;

• t – критерий достоверности или доверительный коэффициент. Он может быть задан с разными степенями точности и в зависимости| от вероятности безошибочного прогноза составлять t = 2 и t = 3.

Средняя ошибка позволяет определить доверительные пределы, в которых с определенной вероятностью находится истинное значение показателя. Интервал, размещенный между ними, называется доверительный интервал (t_˟m).

Границы |граница| достоверности (доверительные границы|граница|):

• Р ± 2m| (при t = 2) дают возможность определить пределы|границу| колебания показателя с вероятностью 95,5 % (р = 0,05);

(t = 2 является округленным результатом. Точное

значение t = 1,96);

• Р ±3m| (при t = 3) дают возможность определить пределы|границу| колебания показателя с вероятностью 99,7 % (р = 0,01).

Не менее важным, чем знание сути параметрического критерия достоверности t, есть осознание значения риска погрешности Р, которое нуждается в понимании логики проверки статистической гипотезы.

Р – это вероятность достоверности нулевой гипотезы или вероятность погрешности, а именно погрешности первого типа – ошибочное утверждение существования расхождений, которых в действительности нет.

Вероятность безошибочного прогноза (p) и доверительный критерий (t) определяют на этапе планирования статистического исследования.

При заданных степенях вероятности доверительный критерий (t) имеет неизменную|неизменяемую| величину, а доверительный интервал (tm) зависит от величины средней ошибки (m), значение которой|какой| уменьшается при увеличении числа и качественного состава наблюдений.

В медико-биологических исследованиях часто возникают ситуации, когда при сравнении отдельных параметров необходимо оценить существенность (достоверность) разницы между ними.

Существенная разница между отдельными показателями выборочного исследования свидетельствует о возможности перенесения полученных выводов на генеральную совокупность.

Параметрическим критерием оценки существенности разности является коэффициент достоверности (критерий Госсета (Стьюдента):

для средних величин;

для относительных величин

При |n > 30 разность |разность| между показателями является существенной, если:

1. t > 2 (отвечает достоверности безошибочного прогноза 95,5 %);

2. t > 3 (отвечает достоверности безошибочного прогноза 99,7 %).

При условии t<2| степень достоверности безошибочного прогноза составляет менее|меньше| 95 %. В этом случае мы не можем утверждать, что разница|разность| между показателями является существенной.

Часто при клинических или экспериментальных исследованиях приходится иметь дело с малыми наблюдениями (если исследование правильно организовано, отобраны однородные группы, которые можно использовать, как выборочные с малым числом наблюдений). Но при n<30 оценка достоверности разницы между параметрами отдельных групп проводится на основе сравнения результата не с предельными значениями критерия Госсета (Стьюдента), а с его табличными значениями для соответствующего числа степеней свободы (n^`= n₁+ n₂ - 2).

Если определенный t-критерий превышает табличное значение— разница между показателями становится статистически доказана.

Критерий достоверности (t) используют при попар­ном| сравнении исследуемых параметров.

Однако при проведении статистического анализа иногда необходимо оценить|оценивать| достоверность разницы|разности| более двух показателей клинико-статистических| групп. Их попарное сравнение не позволяет получить обобщающую оценку. Другими словами, необходимо провести сравнение совокуп­ности| не только по обобщающим показателям, но и по характеру распределения|деления| признаков в исследуемых группах. Для данной цели используют другие критерии.