
- •Курсовая работа
- •Введение
- •Функция. Определение функции
- •Способы задания функции
- •График функции
- •Системы координат
- •Непрерывность функции
- •Точки разрыва
- •Область определения функции
- •Производная функции
- •Интеграл функции
- •Описание программы
- •Библиотека .Dll
- •Редактирование библиотеки функций для построения графиков
- •Руководство пользователя
- •1. Краткое описание возможностей
- •2. Уровень подготовки пользователя
- •3. Подготовка к работе
- •4. Порядок работы с программой
- •Заключение
- •Список использованных источников
График функции
График функции
— множество точек, у которых абсциссы
являются допустимыми значениями
аргумента
 ,
а ординаты — соответствующими значениями
функции
,
а ординаты — соответствующими значениями
функции
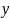 .
.
Обычно рассматриваются
графики вещественных скалярных функций
одного вещественного переменного
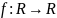 ,
которые являются множеством точек
плоскости
,
которые являются множеством точек
плоскости
 .
.
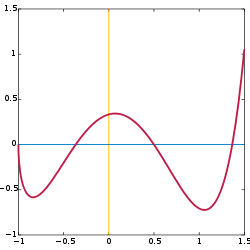
Рис.2 – “График
функции

Системы координат
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае.
Основные системы:
Декартовы координаты
Расположение точки
P на плоскости определяется
декартовыми координатами с помощью
пары чисел
 :
:
— расстояние от точки P до оси Oy с учетом знака;
— расстояние от точки P до оси Ox с учетом знака.
В пространстве же
необходимо уже 3 координаты
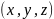 :
:
— расстояние от точки P до плоскости Oyz;
— расстояние от точки P до плоскости Oxz;
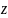 — расстояние от
точки P до плоскости Oxy.
— расстояние от
точки P до плоскости Oxy.
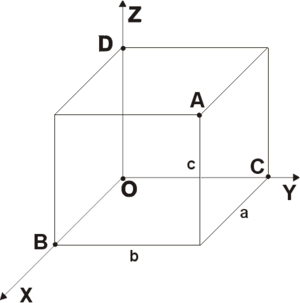
Рис.3 – “Декартовы координаты в пространстве”
Полярные координаты
В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.
Термин «полярные координаты» используется только на плоскости.
 – радиус-вектор;
– радиус-вектор;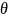 - угол поворота
радиус-вектора.
- угол поворота
радиус-вектора.
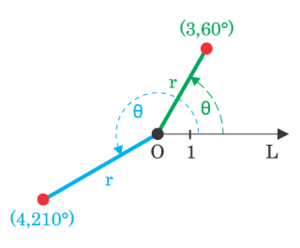
Рис.4 – “Полярные координаты”
Примечание: в данной курсовой работе используется декартова система координат на плоскости.
Непрерывность функции
Непрерывная функция в математике — это отображение из одного пространства в другое, при котором близкие точки области определения переходят в близкие точки области значений.
Пусть,
 .
Функция
непрерывна в точке
.
Функция
непрерывна в точке
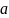 ,
если для любого числа
,
если для любого числа
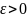 найдётся такое число
найдётся такое число
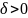 ,
что для всех точек
,
что для всех точек
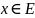 условие
условие
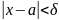 влечет
влечет
 .
.
Другими словами,
функция
непрерывна в точке
,
предельной для множества
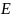 ,
если она имеет предел в данной точке и
этот предел совпадает со значением
функции в данной точке:
,
если она имеет предел в данной точке и
этот предел совпадает со значением
функции в данной точке:
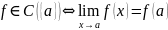 .
.
Функция непрерывна на множестве , если она непрерывна в каждой точке данного множества.
Точки разрыва
Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв.
Существует 3 типа точек разрыва:
Устранимые точки разрыва
Если предел функции
существует, но он не совпадает со
значением функции в данной точке:
 тогда
точка
называется точкой устранимого разрыва
функции
.
Если «поправить» функцию
в точке устранимого разрыва и положить
тогда
точка
называется точкой устранимого разрыва
функции
.
Если «поправить» функцию
в точке устранимого разрыва и положить
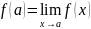 ,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением функции
до непрерывной, что и обосновывает
название точки, как точки устранимого
разрыва.
,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением функции
до непрерывной, что и обосновывает
название точки, как точки устранимого
разрыва.
Точки разрыва первого рода
Если предел функции в данной точке отсутствует и функцию нельзя доопределить до непрерывной и если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода.
Точки разрыва второго рода
Если предел функции в данной точке отсутствует и функцию нельзя доопределить до непрерывной и если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
Примечание: в данной курсовой работе реализована обработка точек разрыва функций.
