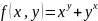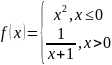Введение

Задание:

Реализация класса графиков вещественных функций вещественного аргумента с масштабированием и скроллингом (набор функций берется из подключаемой библиотеки).

Подробная постановка задачи:

1. Разработать графическое приложение построения графиков вещественной функции вещественного аргумента;

2. Реализовать возможность масштабирования графика при помощи колёсика мыши;

3. Реализовать возможность скроллинга при помощи мыши путём захвата и перетаскивания, а также при помощи точного задания координат просмотра;

4. Реализовать возможность экспорта построенного графика в изображение формата *.bmp;

5. Реализовать возможность подключения dll-библиотеки с набором функций для построения графиков.

Цели:

• Совершенствование навыков ООП;

• Повторение теории пределов;

• Изучение способов связывания;

• Получение навыков по написанию dll-библиотек.

Методы решения:

• CodeGear RAD C++ Builder

• Microsoft Visual C++

Функция. Определение функции

Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

В теоретической математике функцию 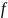удобно определить как бинарное отношение (то есть множество упорядоченных пар 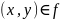), которое удовлетворяет следующему условию: для любого 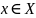существует единственный элемент 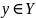такой, что .

Если задана функция , которая определена на множестве 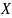и принимает значения в множестве 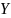, то есть, функция отображает множество в , то:

• этот факт коротко записывают в виде 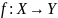или ;

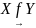• область определения функции (множество ) обозначается ;

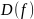• область значений функции (множество ) обозначается .

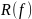Определение функции легко обобщить на случай функции многих аргументов.

Если множество представляет собой декартово произведение множеств 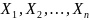, тогда отображение оказывается n-местным отображением, при этом элементы упорядоченного набора 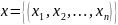называются аргументами (данной n-местной функции), каждый из которых пробегает своё множество: 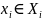где 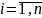. В этом случае 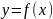означает, что .

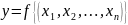Примечание: в данной курсовой работе рассматриваются вещественные функции одного вещественного аргумента.

Способы задания функции

1. Аналитический способ

Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.

• 

• 

2. Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них.

x	0	1	2	3	4	5	6	7	8
y=f(x)	0	1	3	7	15	31	63	127	255

3. Графический способ

Функцию можно задать графически, отобразив множество точек её графика на плоскости. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых удобных для восприятия и анализа функции.

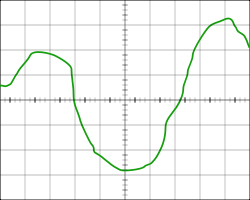
Рис.1 – “Графический способ задания функции”

4. Рекурсивный способ

Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.

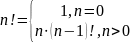
Примечание: в данной курсовой работе реализованы аналитический и графический способы задания функций.