2.5.3. Местные ошибки шага растров

Местной составляющей ошибки шага называется разность между ошибкой шага и ее регулярной составляющей. Местная составляющая ошибки имеет случайный характер и статически равномерно распределена вдоль растра. При нормальной работе делительной машины такую ошибку невозможно учесть или исправить. У существующих делительных машин величина местной ошибки равна 0,4–0,5 мкм.

Причины возникновения местной ошибки обычно кроются в непостоянстве усилий трения в кинематических узлах делительных машин, в их загрязненности, а также в результате колебаний и вибраций отдельных частей делительных машин и т. п.

Кроме статически равномерно распределенной местной ошибки, встречаются еще грубые ошибки случайного характера, которые возникают из-за нарушения режима работы делительной машины, например из-за неточной настройки храпового механизма подачи. Эта ошибка может также возникнуть из-за сдвига заготовки в процессе нарезания растра, плохого крепления резца, резких внешних вибраций и других непредвиденных причин. Для обнаружения местных ошибок можно также пользоваться комбинационными полосами, составляя сопряжение из эталонного и исследуемого растров.

На рис. 11 приведена фотография комбинационного растра, составленного из решеток с шагом 0,05 мм. На комбинационных полосах отчетливо видны грубые местные ошибки.

Обычно грубые ошибки имеют большую величину и решетки при их наличии бракуются.

Рис. 11. Местные ошибки шага растров.

Как отмечалось в предыдущих параграфах, центрированная ошибка не содержит сглаженной составляющей. Математическое ожидание такой случайной последовательности равно нулю.

Для нахождения составляющей местной ошибки необходимо из центрованной составляющей вычесть периодическую составляющую ошибки. Периодическая составляющая определяется по спектру центрированной случайной последовательности.

В силу того, что математическое ожидание центрированной функции

с вероятностью единица, и если дисперсия центрированной ошибки на длине растра постоянна [D(∆g_Ц) = const], эта последовательность на длине L является стационарной в широком смысле и обладает эргодичностью.

Учитывая эргодическое свойство центрированной последовательности ошибки растровой меры, ее можно изучать по одной реализации, т. е. по аттестату одного растра достаточной длины. Изучение ц ентрированной ошибки в основном сводится к вычислению ее дисперсии, корреляционной функции и к определению спектра центрированной ошибки с целью выявления периодической составляющей.

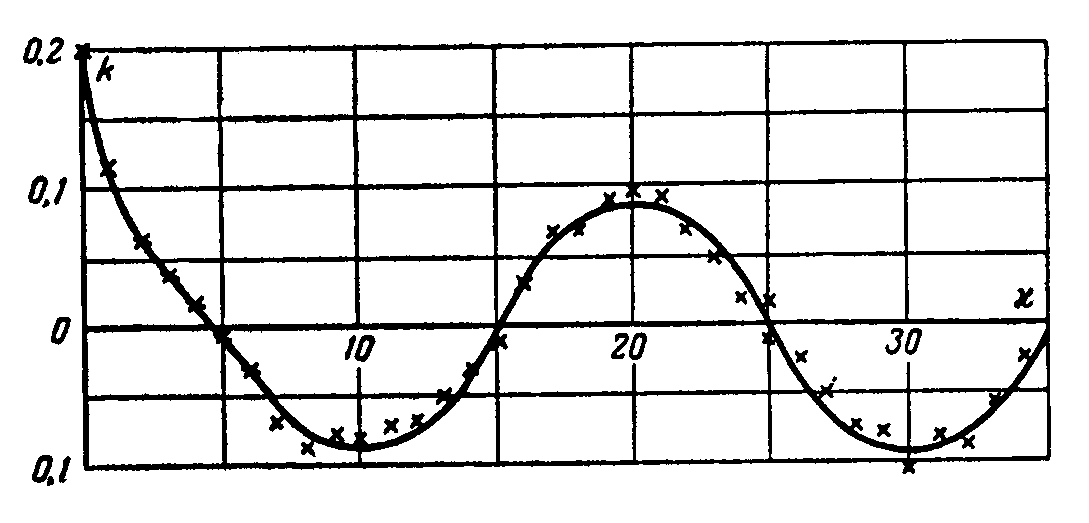
Рис. 12. Корреляционная функция ошибки шага.

Корреляционная функция центрированной случайной последовательности вычисляется по формуле

(20)

где m=0,1,2…

Вычисление значений корреляционной функции производится до таких значений, когда k(∆g_Ц) становится практической равной нулю или стационарной.

При m=0 корреляционная функция равна дисперсии центрированной ошибки:

Корреляционная функция ошибок шага одного из растров, вычисленная по формуле (20), представлена на рис. 12.

Для нахождения спектра местной ошибки ее корреляционная функция аппроксимируется зависимостью, близкой к экспериментальной. Для полученной экспериментальной корреляционной функции наиболее подходит функция

(21)

Параметр = 0,257 найден по методу наименьших квадратов.

Спектральная плотность случайной функции связана с ее корреляционной функцией следующими зависимостями:

;

(22)

.

(23)

Эти зависимости выражают функциональную связь и . Формула (22) выражает корреляционную функцию через спектральную плотность, а формула (23), наоборот, спектральную плотность через корреляционную функцию. Под и подразумеваются нормированные корреляционная функция и спектральная плотность.

Из графика спектральной плотности центрированной ошибки следует, что в ее составе имеется периодическая ошибка с периодом 1 мм. Эта периодическая ошибка имеет большое удельное значение по сравнению со сглаженной и центрированной ошибками.

Вычисление местной составляющей производится по формуле