2. Законы идеальных газов: Бойля-Мариотта, Гей-Люссака, Авогадро, Дальтона..

Закон Бойля-Мариотта: При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно. Формула: pV = const (Изотермический процесс)

Закон Гей-Люссака:при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре. Формула: V/T=const (Изобарный процесс)

З акон Авогадро: 1 Киломоль любого газа занимает при одинаковых условиях одинаковый объём. При норм.условиях (t=0, Р=10^5 Па) V =22.4 м^3. Закон Дальтона: Давление смеси газов равно сумме парциальных давлений.

Закон Шарля : (Изохорный процесс V=const ). P/V=const. , Т- абсолютная температура (t+273)

3. Внутренняя энергия идеального газа. Степени свободы. Теорема о равномерном распределении кинетической энергии по степеням свободы.

В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Формула: 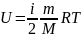Степени свободы- это число независимых координат, которые необходимо задать для определения положения тела в пространстве. Одноатомный – i=3;2-х - i=5; 3-х - i=6 ; Теорема о равномерном распределении кинетической энергии по степеням свободы- В состоянии термодинамического равновесия на каждую степень свободы движения частиц вещества приходится кинетическая энергия в среднем, равная kT/2. (многоатомная молекула Ек=i/2KT).

4. Основное уравнение молекулярно-кинетической теории. Средняя кинетическая энергия молекул, молекулярно-кинетический смысл температуры.

Основное уравнение МКТ связывает макроскопические параметры газовой системы с микроскопическими.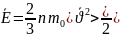 ,где Е-Ек ,n-концентрация молекул 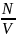, k = 1.38*10^-13 Дж/К –постоянная Больцмана.

Средняя кинетическая энергия поступательно движения молекул:

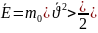
Температура определяется через микроскопические характеристики системы и служит мерой энергии неупорядоченного движения частиц.

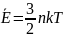
5 .Функция распределения молекул по скоростям. Распределение Максвелла.

,где m0 – масса одной молекулы, exp(e) – основание натуральных логарифмов (е = 2,72). К- постоянная Больцмана.

У всех молекул разные скорости. При столкновении эти скорости изменяются. Распределение Максвелла - распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию.

6.Идеальный газ в поле силы тяжести. Барометрическая формула.Распределение Больцмана.

В идеальном газе, находящемся во внешнем поле сил, каждая отдельная частица приобретает импульс в направлении силы, а также соответствующую потенциальную энергию. Однако в газе наряду с упорядоченным движением в направлении действия силы существует хаотическое тепловое движение. В результате конкуренции между этими двумя типами движений возникает неравномерное распределение макроскопических параметров: плотности частиц, давления, температуры по объему, занимаемому газом.Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.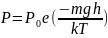 . применима для разреженных смесей газов. В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. 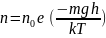В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана: , где е- основание натуральных логарифмов. (2.72).