1.4 Построение аппроксимационных зависимостей методом наименьших квадратов

П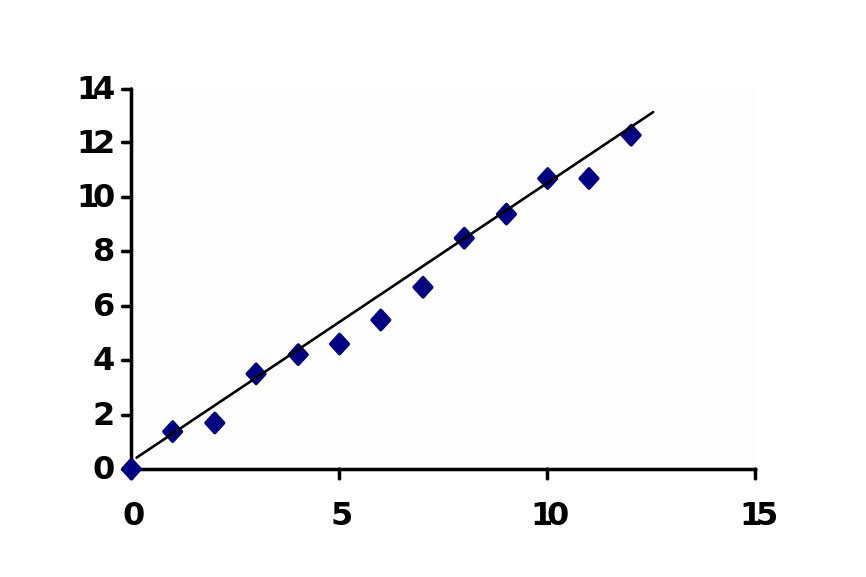 ри аналитическом представлении функциональной зависимости между факторами и откликом необходимо подобрать такую формулу, чтобы случайные отклонения экспериментальных точек не влияли на результат, и случайный разброс отклика под влиянием малозначимых факторов не учитывался, т.е. чтобы искомая формула позволяла получить некий усредненный вариант (рис. 3).

Рис. 3 Экспериментальные точки и аппроксимационная зависимость.

Один из наиболее употребительных методов – "метод наименьших квадратов". Он заключается в подборе коэффициентов зависимости (2) таким образом, чтобы сумма квадратов измеренных значений от расчетных принимала наименьшее значение.

, (7)

где и y_i – экспериментальное и расчетное, полученное по аналитической зависимости, значения отклика, соответственно, i – номер точки, n – количество точек. Отыскание тех значений параметров, которые доставляют наименьшее значение S, сводится к решению системы уравнений

; ; ; ; (8)

Решая систему уравнений, определяем соответствующие коэффициенты и получаем искомую зависимость.

5. Оценка степени влияния качественных факторов

При исследовании качественных факторов зависимости типа (1) и (2) получить нельзя. Поэтому оцениваем факторы по степени влияния их на отклик по принципу "значим - не значим". Для данной оценки проведем серии не менее n (8-10) опытов для каждого уровня фактора. Уровнем фактора является его качественная характеристика: тип подвеса (гибкий/жесткий), квалификация оператора (высокая/низкая) и возраст оператора (по 2 категориям). Полученные данные представляются в виде таблицы (табл. 1).

Таблица 1

Результаты замера отклика

Опыт	Уровень фактора
	1	2
1.	y1,1	y2,1
2.	y1,2	y2,2
…
n	y1,n	y2,n

Для оценки степени влияния фактора на отклик воспользуемся методами дисперсионного анализа. В основе дисперсионного анализа лежит следующее соотношение

(9)

где i и j – номера уровня и опыта, m и n –количество уровней фактора и количество опытов, <y> - общее среднее, <y_i> - уровневое (вычисленное при данном, i-том уровне фактора среднее значение отклика) среднее. Обозначив суммы квадратов через S, получим

. (10)

Поделив каждую из сумм на соответствующие степени свободы, получаем выражения для определения дисперсий

. (11)

Общая дисперсия характеризует общий разброс значений отклика, факторная дисперсия - изменение отклика под влиянием изменения фактора, остаточная дисперсия – случайный разброс отклика. Сравнивая две последних дисперсии между собой, определяем случаен или закономерен разброс отклика при изменении фактора

. (12)

Полученное значение (отношение дисперсий) называется критерием Фишера и сравнивается с табличным (критическим) значением критерия. При желаемой надежности вывода и числах степеней свободы и критическое значение составляет 3.84. Если выполняется условие

, (13)

то изменение отклика при изменении фактора не случайно и этот фактор значим.