§12. Закон распределения случайной функции. Характеристики случайной функции

Как уже отмечалось выше, случайная функция при фиксированном значении аргу­мента t представляет собой обычную случайную величину Х(Ь) . Обозначим плот— Юсть распределения случайной величины в 1Т —ном сечении f [зс(£ц)] ~ f L^»t] , соторую принято называть одномерным законом распределения случайной функции. )чевидно, что одномерный закон распределения f ЈX(t.)] не является полной, ис— .ернывающей характеристикой случайной функции X ("fc) • Бо.лее полной характерис-икой случайной функции является составленный для двух сечений закон распределе— ия f [,dCi ,X₂ , t _л , "t 2.1 ■ Ещ^е более полной характеристикой является трех— 1ерный закон распределения f [ Х₁ ,Х₂ , Х₃ ,t, , t _г , t 3 1 • Это значит, что за­лп распределения случайной функции является законом распределения системы 1*—случайных величин.Пользоваться указанным законом практически весьма пеудоб-;о.В связи с этим, при исследовании случайных функций (случайных процессов) ог-'аиичиваются временными числовыми характеристиками, аналогичными числовым ха-акгернстикам случайных величин. Рассмотрим их.

. Математическое ожидание случайной функции

( 2. Дисперсии случайной функции

Дисперсией случайной функции называется такая неслучайная функция» которая три каждом фиксированном значении аргумента равна дисперсии соответствующего зечения случайной функции, т.е.

Математическим ожиданием случайной функции называется такая неслучайная фикция, которая при каждом фиксированном значении аргумента "t равна матема-'ическому ожиданию соответствующего сечения случайной функции, т.е.

При этом среднее квадратическое отклонение случайной функции равно

Среднее квадратическое отклонение характеризует разброс случайной функции относительно ее математического ожидания. Например, для нормально распределен­ной случайной функции интервалы, равные ± 3 6f_x(fc),образуют собой коридор, внут­ри которого заключено 99,7% всех реализаций случайной функции (см. рис. 5).

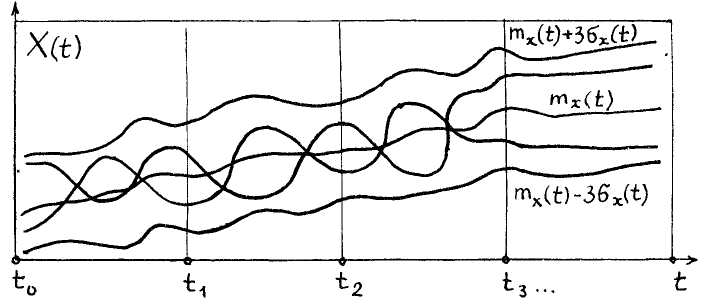
Рис. 5.Иллюстрация "коридора" реализаций случайной функции,

распределенной нормально

3. Корр е ляционная фу нк Ци я i

Корреляционной функцией случайной функции X (t) называется неслучайная <

функция двух аргументов К_х (t,t') > которая при каждой паре значений аргу— j ментов t , t' равна корреляционному моменту соответствующих сечений случайно^ функции

Когда аргументы случайной функции совпадают t = t , то в этом случае корре­ ляционная функция превращается в дисперсию случайной величины ,

4. Нормированная корре ля цион ная ф у нкци я ;

Корреляционная функция, отнесенная к произведению средних квадратических от-, клонений, называется нормированной корреляционной функцией j

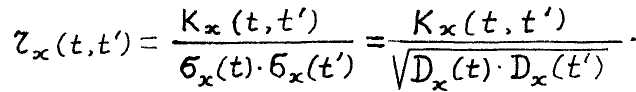
Очевидно, что когда сечения совпадают, то нормированная корреляционная функция ' становится равной единице. i

Таким образом, случайная функция характеризуется: П, -математическими ожи-s даниями, П. - дисперсиями и П.(п-1)/2 - корреляционными функциями.

Все корреляционные функции случайной функций удобно расположить в виде прямо угольной таблицы, т.е. в виде так называемой матрицы.

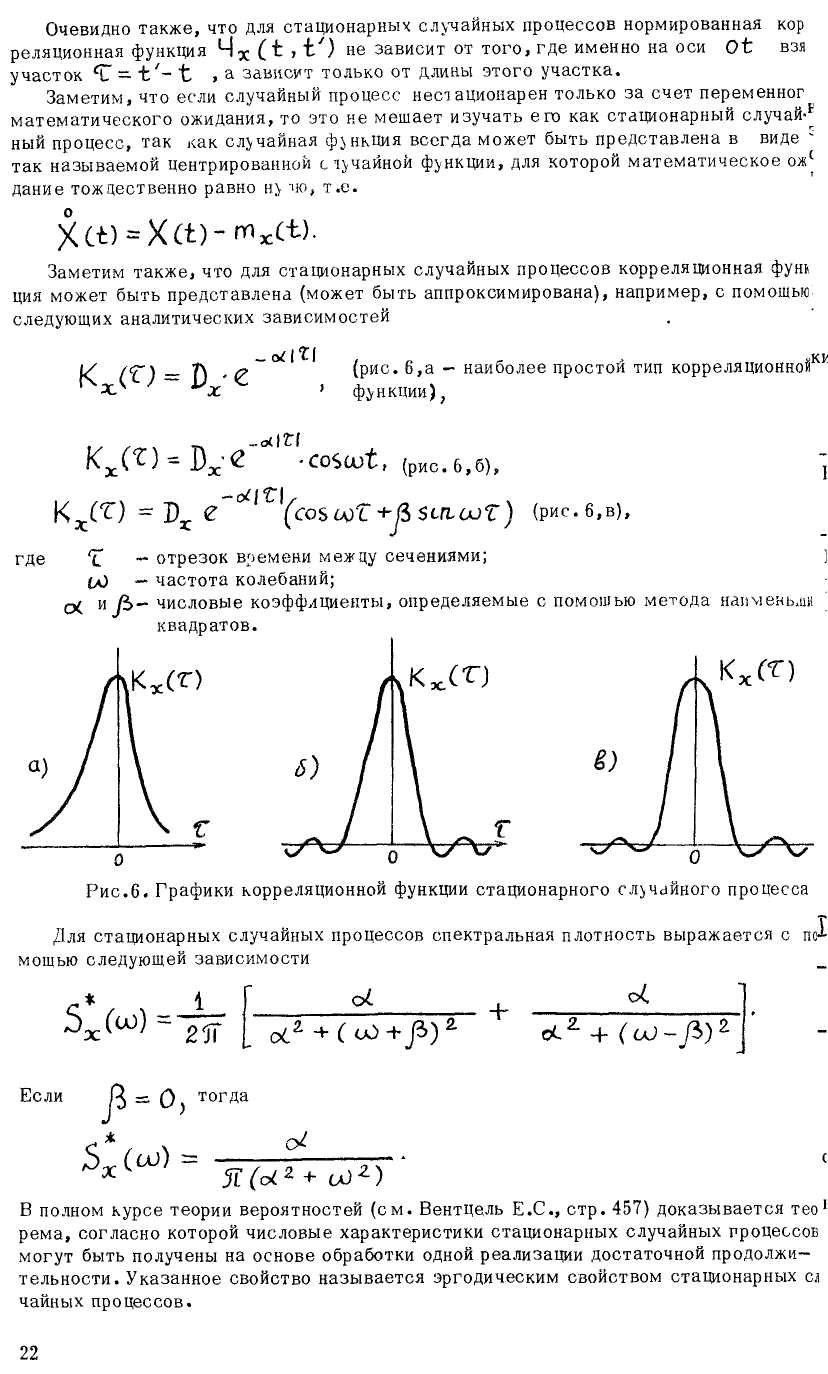
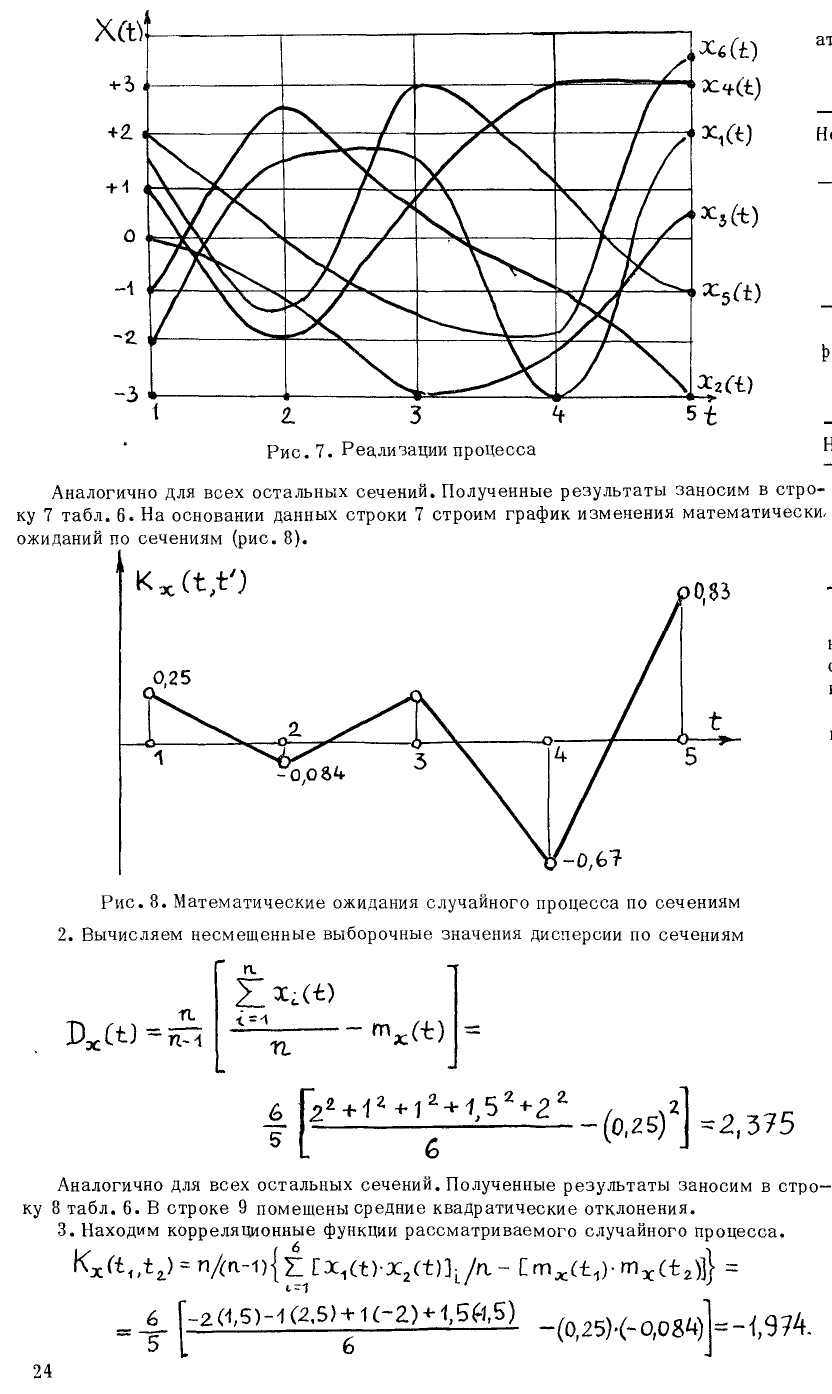
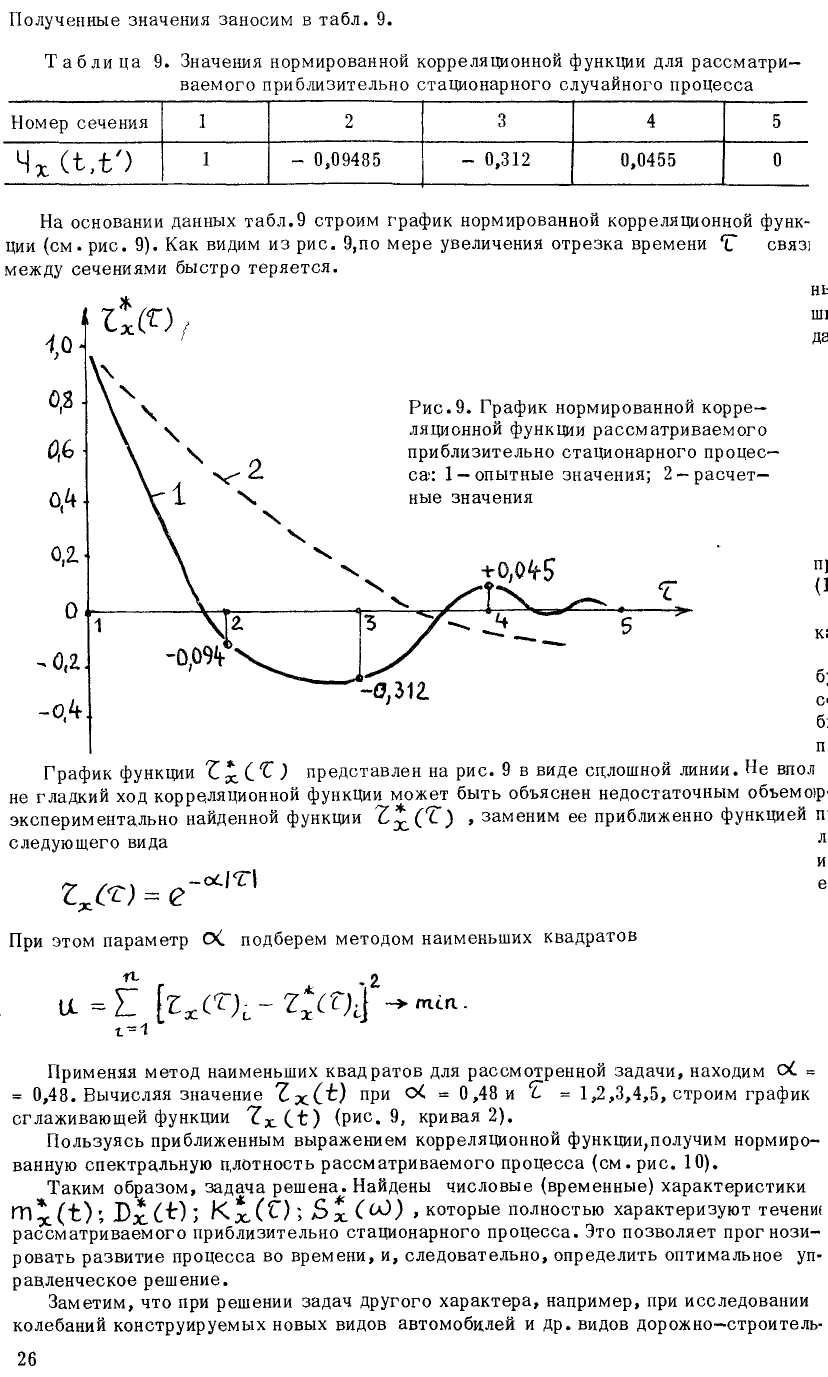
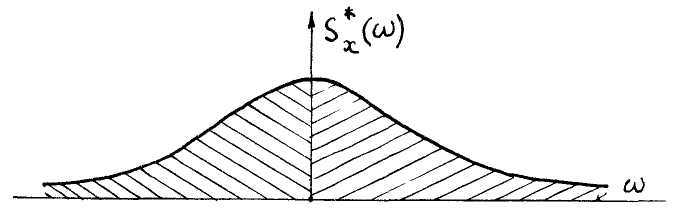
Рис.10. График нормированной спектральной плотности для рассматриваемой задачи

i ных машин, расчет корреляционной функции и спектральной плотности позволяет ре— j шить задачу выбора оптимальной конструкции подвески и решить другие подобные за­дачи.