§10. Принятие решения в условиях полной неопределенности, когда вероятности внешних условий неизвестны

Кроме рассмотренных выше случаев (§§8 и 9)_;b практике решения задач могут иметь место такие ситуации, когда известны значения выигрышей для различных внеш­них условий, однако вероятности указанных внешних условий неизвестны. В этом слу­чае, для определения оптимальных решений применяются рассматриваемые ниже мето­ды или подходы, предложенные Вадьдом, Сэвиджем и Гурвицем. Рассмотрим указан­ные методы.

1. Максминный метод Вальда

Для определения оптимальной стратегии, согласно методу Вальда, в каждой стро­ке табл. 4 вычисляется минимальный выигрыш и из полученных минимальных выигры­шей выбирается максимальный. Решение, отвечающее этому значению, и будет оптимальным, т.е.

[где А опт. ~ оптимальное решение (оптимальная стратегия);

Qi" ~ выигрыши, отвечающие различным стратегиям, вычисленные для раз—

^с* личных внешних условий.

Проиллюстрируем применение указанного метода на примере. Предположим, что 'для четырех возможных стратегий при различных внешних условиях были подсчитаны значения выигрышей (см. табл. 4). Требуется, применяя метод Вальда. определить оптимальную стратегию.

Таблица 4. Определение оптимальной стратегии согласно методу Вальда

Решения, стра­тегии, альтер-	внешние условия и отвечающие hn выигрышей для каждой стратегии		значения	Mit-ijl
нативы, виды продукции	Глина	Песок	Супесь
	П	У2	уз
Х1	ап=0,20	а 12 = 0,30	а13-0.15	aj = 0,15
\ Х£	а 21= 0,75	а 22 = 0,20	а 23 = 0,35	а2= 0,20
Х3	а 31= 0,25	а32=0,80	азз-0,75	а з = 0,25
Х4	а 41= 0,85	а42 = 0,05	а43=0,45	а4= 0,05

Рассматривая значения, помещенные в последнем столбце таб.л. 4, видим, что наи­большее значение из минимальных выигрышей равно 0,25, что отвечает стратегии Х₃. Это значит, что для рассматриваемой задачи оптимальной, согласно методу Вальда, является стратегия Xj(cm. [6], [14] и др.).Метод Вальда называют методом крайнего пессимизма, так как согласно этому мзтоду "Всегда надо рассчитывать на худшее".

2. Метод минимаксного риска Сэвиджа

Метод Сэвиджа подобен методу Вальда с той лишь разницей, что значения крите­риев эффективности в статистической таб.лице выражаются в величинах риска. Пере­счет величин выигрыша в значения риска производится с помощью приведенной выше формулы (,Е). Так, например, для условий, показанных в табл. 4, имеем

Таб.лица 5

Решения, стратегии, Внешние условия альтернативы, виды Глина Песок Супесь продукции M^LM-] У1 У2 УЗ хх Чп=0,65 Ч12 = 0,50 Ч13 = 0,30 Чг=0,65 х2 Ч21=0,10 Ч22=0,60 Ч2з=0,10 Ч2=0,60 хз Ч31=0,60 Ч32=0,00 Ч33=0Д0 Ч3 = 0,60 х4 Ч41 = 0,0 Ч42 = 0,75 Ч43 = 0,75 Ч4=0,75

Согласно методу Сэвиджа,в каждой строке статистической таб,лицы (табл. 5) вы­числяется максимальное значение риска и из полученных значений выбирается мини­мальный риск. Решение, отвечающее этому значению, и будет оптимальным> т.е.

Как видим, для рассмотренного примера оптимальной стратегией, подсчитанной согласно методу Сэвиджа, является стратегия Х^ или Х^ , т.е. решения, получен­ные с помощью метода Вальда и метода Сэвиджа, совпадают.

Заметим, что метод Сэвиджа, так же как и метод Вальда, является методом край­него пессимизма. Однако пессимизм в случае применения метода Сэвиджа проявляет­ся в том, что из максимальных значений рисков выбирается минимальный.

3. Метод пессимизма—оптимизма Гурвица

Для условий, когда внешние условия не заданы своими вероятностями (случай под-ной неопределенности), оптимальная стратегия может определяться не только с по­мощью методов Вальда и,ли Сэвиджа, но и с помощью метода Гурвица. Метод Гурвица позволяет определять оптимальную стратегию в некотором диапазоне от крайнего пес­симизма до крайнего оптимизма.

Оптимальная стратегия, согласно этому методу,вычисляется по форму.ле

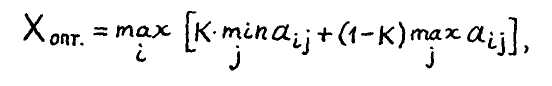
где К - коэффициент, лежащий в пределах 0 $: К 4 Ь Нетрудно видеть, что при К = 1 метод Гурвица преобразуется в метод Вальда. При К = 0 метод Гурвица преобразу­ется в метод крайнего оптимизма. При среднем значении К , например, при 0,4 $• К$ $.0,6 метод Гурвица является средним между методом крайнего пессимизма и крайнего оптимизма.

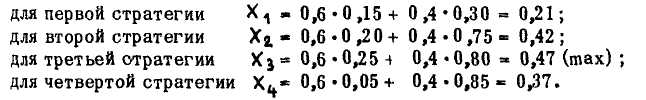
Проиллюстрируем порядок определения оптимальной стратегии, согласно методу Гурвица для условий, показанных в табл. 4, при К = 0,6. Тогда

Как видим, оптимальной, согласно методу Гурвица, является стратегия X ^ .

В главе кратко рассмотрены методы определения оптимальной стратегии для ус­ловий, когда математическая модель исследуемого явления задается в виде статисти­ческой таблицы, в которой для каждой из сравниваемых стратегий и различных внеш­них условий приведены значения частных критериев эффективности системы, выражен­ные в выигрышах и,ли в значениях риска. Указанные методы применяются при сравни­тельном анализе различных видов автомобильных и дорожных средств и систем. В ^частности, при решении задачи о конкурентной способности автомобилей и дорожно­строительных машин Советского Союза.