§9. Принятие решения в условиях стохастической неопределенности, когда внешние условия задаются своими вероятностями

Указанный случай возникает тогда, когда известны значения частных критериев ' эффективности, вычисленные для различных видов внешних условий. При этом из­вестны также вероятности указанных внешних условий. Покажем порядок определения наивыгоднейшей стратегии для рассматриваемых условий. Предположим, что сравниваются четыре вида экскаваторов, изготовляемые различными заводами—изготови­телями. Под внешними условиями подразумеваются виды грунтов, на которых предпо­лагается использовать указанные экскаваторы (см. табл. 2).

Таблица 2. Определение оптимальной стратегии по максимуму математического ожидания выигрыша

Возможные стратегии, решения, аль-	Внешние условия, заданные своими вероятностями,и значения выигрышей для каждой из сравниваемых стратегий
тернативы	Глина	Песок	Супесь	Каменист, грунт
	Pi - 0,1	Р2 - 0,2	Р3=0,3	Р4 = 0,4
Экскаватор завода № 1,х1 Экскаватор завода М2,х2 Экскаватор завода № 3, х3 Экскаватор завода * 4, х4	а и-7 а 21 - 3 а31 = 4 а 41= 1	а12- 5 а 22 = 6 а32 = 3 «42-2	а13- 1 а23 = 3 аЗЗ=5 а43 = 7	а14=2 а24 = 4 а34= 1 а44=6	Mi = 2,8 М2 = 4,0 М3 = 2,9 М4 - 5,0

Находим для заданных условий (табл. 2) математические ожидания выигрыша для каждой из четырех сравниваемых стратегий, например, для первой стратегии имеем

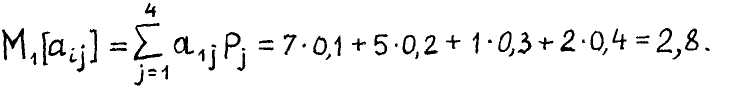
Аналогично для остальных стратегий (см. последнюю колонку табл. 2). Как видим, оптимальным решением является решение Хц. •

С помощью указанной формулы были пересчитаны значения выигрышей, помещен­ные в табл. 2, в величины риска (см. табл.3).

Математическое ожидание риска, например, для первой стратегии составляет:

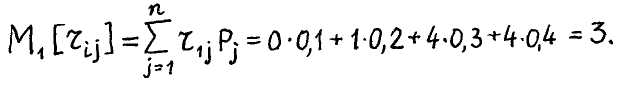
Аналогично для остальных стратегий (см. последнюю колонку табл. 3).

В полном курсе исследования операций доказывается теорема, согласно которой максимум математического ожидания выигрыша эквивалентен минимуму математи­ческого ожидания риска. Пересчет величин выигрыша в значения риска производится по формуле

Таблица 3. Определение оптимальной стратегии по минимуму математического ожидания риска

Возможные ■ стратегии, ре_	Внешние условия, заданные своим4 вероятностями, и риска для каждой из стратегий				значения
i шения, альтер— ! нативы	Глина	Песок	Супесь	Каменист, грунт	М, [Ч;-]
	Pi - 0,1	Р2 - 0,2	Р3 - 0,3	Р4 - 0,4
Х1	Чц = °	Ч12-1	Ч13=4	Ч14=4	«2- 3
Х2	Ч21"4	ч22=о	ч2з=2	Ч24-2	М2-1,8
Х3	Ч31-3	Ч32=3	ч33«о	Ч34=5	М3= 2,9
Х4		Ч42=4	Ч43--2	Ч44=0	М4- 1,1

Из табл. 3 видно, что оптимальной стратегией, вычисленной по математическому ожиданию риска, является стратегия Х^ , т.е. получили тот же результат.