§ 6. Определение оптимальных решений на основе полученных уравнений регрессии

После дискриминации и проверки математической модели на адекватность, т.е. после получения математической модели, которая адекватно описывает изучаемое яв­ление или процесс, приступают к решению основной задачи, т.е. к определению таких значений факторов, при которых функция отклика будет иметь наибольшее (или наи­меньшее) значение. Порядок решения указанной задачи проиллюстрируем на примере. Предположим, что после дискриминации и проверки на адекватность была получена ма­тематическая модель следующего вида

Требуется определить значения факторов Х₁ и Х^ , при которых функция от­клика будет иметь наибольшее значение.

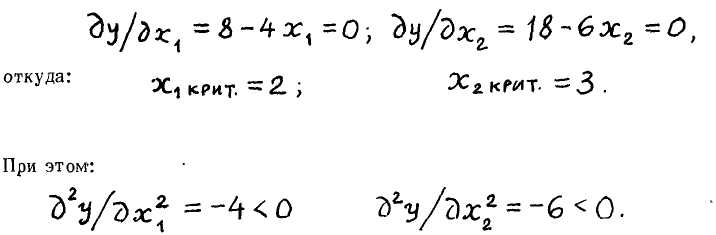
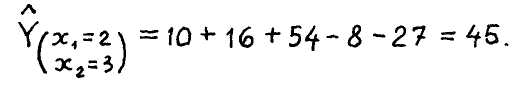
Решение. Дифференцируя функцию у _расч по переменным ЭС, и Х^ и приравнивая производные нулю, получаем:

Следовательно, в критической точке функция отклика имеет максимум, равный:

С помощью уравнений регрессии представляется возможность не только опреде­лять экстремальные значения аргументов, при которых функция отклика имеет мак­симальное или минимальное значение, но и решать следующие задачи:

• ранжировать факторы по их влиянию на функцию отклика; >

• прогнозировать развитие явления или процесса во времени, и, следовательно, решить вопрос об оптимальном управлении (см. [14],[ 19] и др.).

Глава III.

ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ РЕШЕНИЙ ДЛЯ УСЛОВИЙ, КОГДА МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЗАДАЕТСЯ В ВИДЕ ТАБЛИЦЫ

§7. Общие сведения

Как уже отмечалось выше (см. рис. 1),в некоторых случаях математические модели исследуемых явлений или процессов могут быть заданы в виде таблиц, элементами которых являются значения частных критериев эффективности функционирования системы, вычисленные для каждой из сравниваемых стратегий при заданны внешних условиях. Для рассматриваемых условий могут иметь место следующие слу­чаи:

— принятие решения в условиях полной определенности:

а) когда оценка решений производится по одному критерию;

б) когда оценка решений производите?! по нескольким критериям;

• принятие решения в условиях стохастической неопределенности, когда внешние условия задаются своими законами распределения;

• принятие решения в условиях полной неопределенности, когда вероятности внеи них условий неизвестны.

Рассмотрим каждый из указанных случаев.

§ 8. Принятие решения в условиях полной определенности

Для иллюстрации указанного случая предположим, что с помощью статистических наблюдений были подсчитаны значения частных критериев эффективности функциони­рования какого—либо механизма, изготавливаемого несколькими предприятиями—из­готовителями. Пусть это будут бульдозеры, изготавливаемые на трех заводах (см табл. 1).

Примечания: 1. Значения частных критериев даны в условных единицах.

2. Веса частных критериев X : получены на основе экспертных оценок.

Таблица ], Выбор оптимальной стратегии в условиях полной определенности

Варианты механизмов, предлагаемые различны­ми заводами-изготовите­лями, т.е.стратегии,ре­шения, альтернативы	Подсчитанные для каждого v Производи­тельность Е	) значения час [3 предлагаемь Надежность ее частного к] Ло = 3	гных кр IX буль Эконог показ (цена зитерия Л3 =	итери ев дОзеров иический атель изделия) = 2,5	эффективности Энергоем­кость Л4 = 2
Бульдозер завода № 1, x1(i- 1)	аи-2	а12= 3	а13	-7	а14- 5
Бульдозер завода № 2, х2 (i - 2)	а 21-3	а22 = 4	а23	= 5	а24=7
Бульдозер завода № 3; х3 (i = 3)	а 31- 5	а32 = 6	аЗЗ	= 6	а34 = 2

Очевидно, что выбор оптимальной стратегии по одному критерию не вызывает за­труднений. Например, если оценивать бульдозеры по производительности, то лучшим является бульдозер завода № 3.

Затруднения возникают тогда, когда требуется найти оптимальное решение по комп­лексу нескольких критериев. Указанная задача называется многокритериальной. Труд­ности возникают в связи с тем, что частные критерии имеют различную размерность, т.е. являются числами именованными. Для решения указанной задачи вначале произ­водится преобразование частных критериев в безразмерные величины по формулам

где &цом. — номинальное, задаваемое техническими условиями, значение крите­рия;

d _тд_ — значение частного критерия, полученное на основе статистических _ наблюдений;

^6£3р- — безразмерное (нормализованное) значение частного критерия. Формулой (А) пользуются в том случае, если увеличение рассматриваемого част­ного критерия ведет к увеличению обобщенного, т.е. комплексного критерия. В против­ном случае применяется формула (В). Это правило можно сформулировать так: из большего вычитается меньшее и делится на большее.

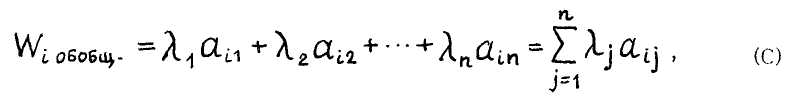
или по формуле взвешенного среднего геометрического

где VV- — суммарный (обобщенный) критерий, вычисленный для I —той

^L * < стратегии.

После перевода частных критериев эффективности в безразмерные величины сум­марный (обобщенный) критерий VV^engm вычисляется по формуле взвешенного среднего арифметического

Применяя формулы (С) и (D), вычисляют для каждой из стратегий значения сум­марного (обобщенного) критерия. При этом стратегия, получившая наибольшее значение обобщенного критерия, и является оптимальной.