§ 41. Проверка согласованности показаний двух экспертов

с помощью коэффициента ранговой корреляции Спирмена

Очевидно, что групповая экспертная оценка может считаться надежной лишь при условии достаточной согласованности ответов экспертов. Если согласованности нет, то в этом случае может иметь место сдвиг среднего арифметического относительно истинного значения, т.е. возникнет ошибка. Это значит, что применяя экспертный ме­тод необходимо проверять согласованность ответов экспертов. Проверка согласован­ности мнений нескольких экспертов может производиться двумя способами:

• с помощью коэффициента ранговой корреляции Спирмена;

• с помощью коэффициента конкордации Кендэла. Рассмотрим порядок проверки согласованности первым методом. Значение коэффициента ранговой корреляции Спирмена составляет

где VI. — число факторов;

ОФАК7-— фактическая сумма квадратов отклонений;

Swkc— максимально возможное значение суммы квадратов отклонений.

При этом, если согласованность показаний двух сравниваемых экспертов хорошая, то коэффициент ранговой корреляции Спирмена стремится к единице, T.e.p^gop-^+i,

Если же согласованность неудовлетворительная, то коэффициент ранговой корре­ляции Спирмена стремится к нулю f выбор ~*~0 -

Проверка согласованности показаний двух экспертов с помощью опытного коэф­фициента ранговой корреляции Спирмена производится согласно дледуюшему альтер­нативному соотношению

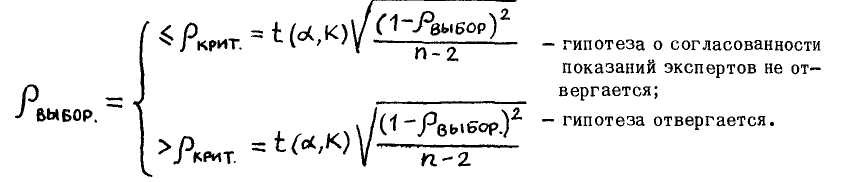
где "t(«,K)— критические точки распределения Стьюдента, вычисляемые при за­данном уровне значимости оС и числе степеней свободы К = П~2< (См.Методические указания по выполнению курсовой работы. 1979г,приложение,табл.17.)

Таблица 24. Матрица попарных сравнений показаний двух экспертов

п/п	Эксперты		Факторы					Сумма
		ф1	Ф2	Ф3	Ф4	ф5	Ф6	рангов
1 2 3 4	Первый эксперт Второй эксперт Отклонения оценок Aj Квадраты отклонений	1 3 2 4	2,5 1 1,5 2,25	4 2 2 4	2,5 4 1,5 2,25	6 5 1 1	5 6 1 1 ...	21 21 14,5

Покажем на примере порядок проверки согласованности показаний двух экспертов, например, показаний первых двух экспертов, оценки которых приведены в табл.23.

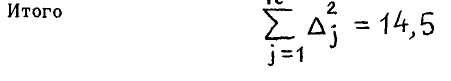
Пример 22. В условиях предыдущей задачи (табл.23) вычислить при уровне значи­мости О(- = 0,0 5 коэффициент ранговой корреляции Спирмена для первых двух экспер­тов и на основе этого оценить согласованность их показаний.

Решение

1. Составляем таблицу попарных сравнений показаний первых двух экспертов (см.

табл.24).

2. Вычисляем опытное значение коэффициента ранговой корреляции Спирмена

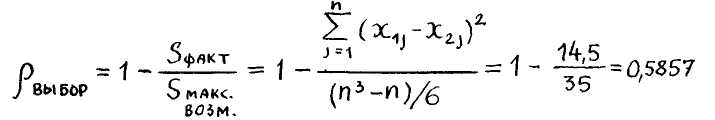
3. Находим, по табл. Стьюдента, критическое значение коэффициента

Следовательно, гипотеза о согласованности показаний двух экспертов для рассмот­ренного примера, вычисленная с помощью коэффициента ранговой корреляции Спирме— на не отвергается.

В таком порядке поочередно сравнивается согласованность показаний двух экспертов: первого со вторым, с третьим и с четвертым; второго с третьим и четвертым и наконец, третьего с четвертым. Полученные значения коэффициентов ранговой корреляции заносят в таблицу. Предположим, что при этом были получены следующие значения коэффициентов ранговой корреляции Спирмена (см. табл.25).

Таблица 25. Матрица коэффициентов ранговой корреляции Спирмена, составленная на основе попарного сравнения показаний четырех экспертов

Эксперты	Эксперты
	1	2	3	4
1	1	0,58	0,8	0,09
2	0,58	1	0,6	0,04
3	0,8	0,6	1	0,02
4	0,09	0,04	0,02	1

Из табл. 25 видно, что коэффициент ранговой корреляции Спирмена четвертого эксперта значительно отличается от аналогичных коэффициентов первого, второго и третьего экспертов. Необходимо анонимно ознакомить экспертов с результатами пер­вого тура опроса и приступить ко второму туру. Очевидно, что ознакомившись с ре­зультатами первого тура четвертый эксперт изменит свои показания и этим самым приблизится к объективному коллективному мнению.

Примечание. Кроме рассмотренного выше попарного сравнения показаний двух экспертов по нескольким факторам, в некоторых задачах применяется сравнение показаний группы экспертов по двум факторам.