Глава IX.

ПРИМЕНЕНИЕ ЭКСПЕРТНОГО МЕТОДА ДЛЯ ОПРЕДЕЛЕНИЯ ВЕСОВ ЧАСТНЫХ ПОКАЗАТЕЛЕЙ ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ АВТОМОБИЛЬНО-ДОРОЖНЫХ СРЕДСТВ И СИСТЕМ

§40. Общие сведения

При исследовании различных процессов с задачей определения оптимальных реше­ний часто возникают такие ситуации, когда сбор информации о состоянии исследуе­мых объектов затруднен или невозможен. В этом случае приходится полагаться на субъективные мнения экспертов. Экспертный метод применяется в настоящее время в экономике, технике, в военном деле, в медицине и в других областях человеческой деятельности. Работа экспертов может рассматриваться как процесс создания на ос­нове имеющейся неполной информации предполагаемой (эвристической) модели причин­но—следственных связей анализируемого явления или процесса и выработки рекомен­даций для принятия оптимального решения.

С точки зрения теории вероятностей и математической статистики показания (оценки), выдаваемые каждым из экспертов, могут рассматриваться как варианты не­которой выборки из генеральной совокупности. Следовательно, коллективное мнение (коллективная оценка) представляет собой среднее арифметическое по каждому из факторов

где 3C_L) — оценка j —того фактора L—ым экспертом; пч — число экспертов; я — число факторов.

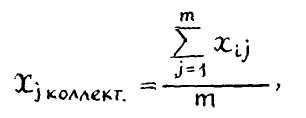
Оценки, выдаваемые экспертами, могут выражаться в виде рангов, приписывае­мых каждому из факторов, или в виде баллов, например, в двухбалльной, трехбалльной, пятибалльной и tjt. системах.

Под рангом прнимают место фактора в ранжировочном ряду. Так, например, если данному фактору приписан ранг, равный единице, то это значит,что он является более весомым, по сравнению с другими факторами, которым приписаны ранги 2,3 и т.д.

При оценке факторов в баллах фактор, получивший наибольший балл, считается доминирующим.

При обработке оценок, выданных экспертами в рангах, должна соблюдаться нор­мировка рангов, т.е. сумма рангов должна быть равна сумме членов натурального ря­да, т.е.

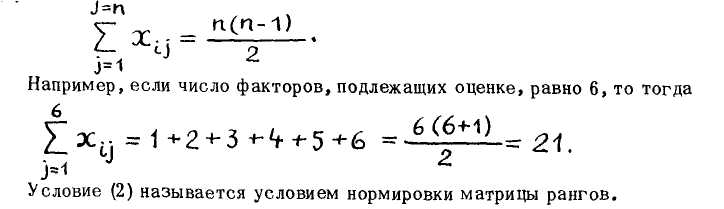
Проиллюстрируем порядок определения коллективного мнения группы экспертов

на примере.

Пример 21. Предположим, что четырьмя экспертами была произведена оценка зна-чимости шести факторов (критериев),применяемых для оценки качества дорожно­строительных машин в рангах (табл. 22).

Табли ца 22. Матрица оценок, составленная на основе показаний четырех экспертов в рангах

Номер	Факторы						Сумма
экспер-	Ф1	Ф2	Ф3	Ф4	*5	ф6	рангов
та	Произво­дитель­ность	Энерго­емкость	Надеж­ность	Ремонто­пригод­ность	Цена из­делия	Техноло­гичность
1 2 3 4	1 3 6 6	2 1 3 6	3 2 1 ■5'	2 4 2 1	5 5 4 2	4 6 5 4	17 21 21 24

Решение

1. Проверяем матрицу оценок на условие нормировки.

Рассматривая табл. 22 видим, что у первого эксперта имеется повторение ран­гов: второй и четвертый факторы делят второе и третье места. Это значит, что у пер­вого эксперта нарушено условие нормировки. Для исправления этого положения произ­водим нормировку рангов. Значения рангов для второго и четвертого фактора вычис­ляем по формуле

2 + 3 =2,5 (см. табл.23).

Из табл. 22 видно также, что у четвертого эксперта первый и второй факторы по­делили пятое и шестое места. Поэтому ранг для первого и второго факторов состав­ляет

5+6 = 5,5 (см. табл.23).

Таблица 23. Нормированная матрица оценок, составленная на основе показаний четырех экспертов

№	—— Эксперты		Факторы					Сумма
п,/п		Ф]	Ф2	Ф3	Ф4	ф5	Фб	ран­гов
1 2 3 4	Первый эксперт Второй эксперт Третий эксперт Четвертый эксперт	1 3 6 5,5	2,5 1 3 5,5	4 2 1 4	2,5 4 2 1	6 5 4 2	5 6 5 3	21 21 21 21
5	Среднее арифмети­ческое, т.е. коллек­тивное мнение груп­пы экспертов	3,875	3	2,75	2,375	4,25	4,75	21
6	Место фактора в ран— жировочном ряду	4	3	2	1	5	6	21

Примечание.. Оценки 2,5 и 5,5 называются связанными.

Ранжировочный ряд не устанавливает величину разности между значимостью фак­торов, а устанавливает лишь их последовательность.