§24. Решение задачи теории массового обслуживания методом статистического моделирования

Покажем на примере порядок решения задач теории массового обслуживания мето­дом статистического моделирования.

Пример 8. Исследуется работа станции технического обслуживания автомобилей, имеющая в своем распоряжении два канала (П. = 2) и два места для ожидания в очере­ди (гп= 2). На станцию поступает простейший пуассоновский поток заявок с плотностью X" 1,5 автомобилей в час, а время обслуживания машин распределено по показатель­ному закону и составляет в среднем И -^ _Обсл.⁼ 2,5 часа на один автомобиль. Требует­ся, применяя метод статистического годелирования, определить числовые характе­ристики функционирования станции за один 10-часовой рабочий день. При моделиро­вании времени поступления заявок воспользоваться строкой 1 табл.12, а при модели­ровании времени обслуживания воспользоваться строкой 2 той же таблицы, начиная, например, с третьего чицла.

Решение. 1. Строим граф состояний системы (см. рис. 20).

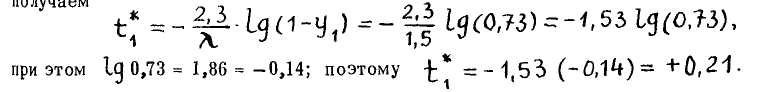
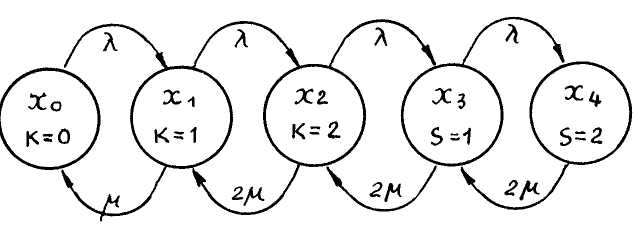
2. Моделируем время поступления заявок. Для первого случайного числа "У| - 0,27,

Рис. 20. Граф состояний системы массового обслуживания с ожиданием, имеющей в своем распоряжении 2 канала и 2 места для ожидания в очереди

Аналогичными расчетами получаем значения промежутков времени между двумя последующими (соседними) автомобилями

Полученные значения заносим в таблицу (см. табл.13).

Табли ца 13. Расчет моментов времени прибытия автомобилей на станцию технического обслуживания

Номер машины	1	2	3	4	5	6	7	8	9	10	11 '
Случайные чис­ла	0,27	0,76	0,74	0,35	0,84	0,30	0,18 С	,89	0,77	0,29	0,49
Промежуток времени меж­ду двумя ма­шинами At*t	0,21	0,95	0,90	0,29	1,22	1,26	0,24	3,13	1,47	0,98	0,23
Момент прибы­тия машины	0,21	1Д6	2,06	2,35	3,57	4,83	5,07	5,20	6,17	7,65	7,88

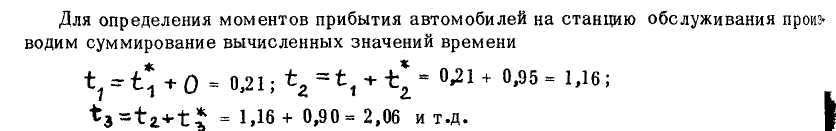
Полученные значения моментов времени прибытия машин на станцию технической обслуживания откладываем на графике (см. рис. 21).

3. Моделируем с помощью алгоритма "А" время, расходуемое на обслуживание каждой очередной машины. Случайные числа г) , отвечающие строке второй табл.11 составляют: 0 ,51; 0,43; 0,38 и т.д.

Для этого вначале вычисляем плотность или интенсивность обслуживания

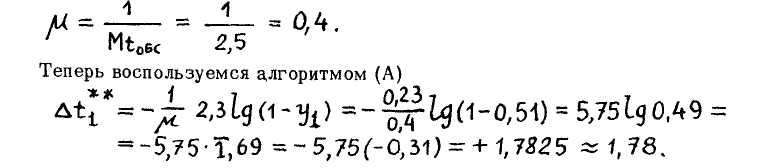
Полученное значение времени Д."Ь _л == 1,78 заносим в табл.14. Аналогично вычио. \ ляем значение времени обслуживания для остальных машин. Учитывая время прибытия машин и время, расходуемое на их обслуживание, вычисляем моменты начала и конца обслуживания для каждой из машин (см. табл. 141.

Табли ца 14. Расчет моментов начала и конца обслуживания автомобилей на станции технического обслуживания

Номер машины	1	2	3	4	5	6	7	8	9	10	11	12
Случайные числа у•	0,51	0,43	0,38	0,54	0,06	0,61	0,52	0,43	0,47	0,72	0,46	0,67
Время обсл.	1,78	1,4	1,2	1,94	0,15	2,35	1,83	1,4	1,59	3,18	1,54	2,77 !
Нач. обсл. L l нач.	0,21	1,16	2,06	2,56	3,57	4,83	5,07	6,9	7,18	8,3	8,77	маш. вы д. отк.
Конец обсл. X V КОН.	1,99	2,56	3,26		3,72	7,18	6,9	8,3	8,77	11,48	10,31	маш. выд. отк.

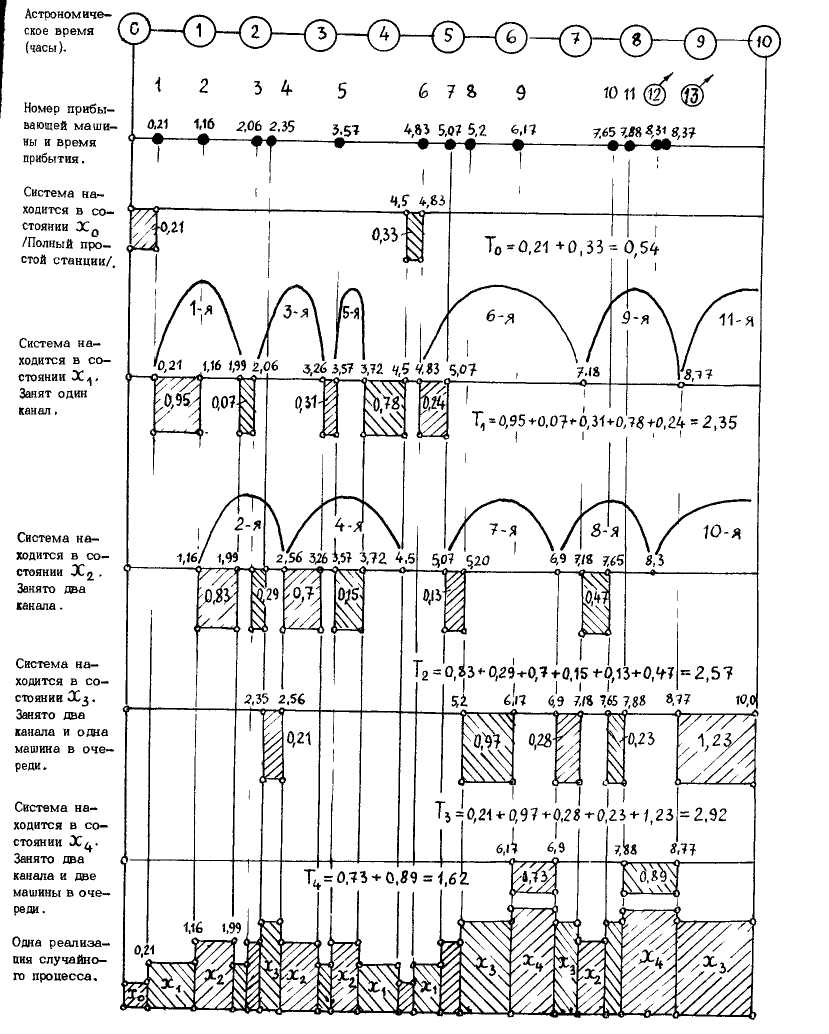
Рис.21. График расчета времени состояний системы массового обслуживания, имеющей два канала и два места для ожидания в очереди. Л= 1,5 авт в час и М. ₀₆, = 2,5 ч.

Полученные характеристики отвечают одной реализации процесса, т.е. соответ­ствуют одному рабочему дню работы станции. Для получения более точных результа­тов в зависимости от требуемой точности, число реализаций должно быть увеличено до 100-1000 реализаций. Тогда, осредняя полученные частоты Р* _;Р^ ., Р^* , получа­ют более точные значения математического ожидания числа занятых каналов, мате­матического ожидания длины очереди и др. характеристик. Произведенные в настоя­щем параграфе расчеты выполнены лишь для одной реализации с целью иллюстрации метода.

В заключение отметим, что метод статистического моделирования может приме­няться не только для решения задач теории массового обслуживания, но и для других задач, например :

• для определения надежности функционирования сложных технических систем;

• для определения оптимального количества запасных частей, узлов и агрегатов, необходимых для поддержания заданного парка автомобилей в исправном состоянии;

• для определения пропускной способности автомобильных дорог и для решения других задач (см., например, [18]) и другие.