§22. Теоретические основы метода

Метод статистического моделирования (называемый также методом Монте-Карло) заключается в воспроизведении исследуемого физического процесса при помощи ве­роятностной математической модели и вычислении характеристик этого процесса. Ос­нован этот метод на многократных испытаниях построенной модели с последующей статистической обработкой полученных данных с целью определения числовых харак­теристик рассматриваемого процесса в виде статистических оценок его параметров. Основой метода статистического моделирования является закон больших чисел.

Под законом больших чисел в теории вероятностей понимается ряд теорем, в ко­торых для тех или иных условий доказывается сходимость по вероятности средних зна­чений результатов большого числа наблюдений к некоторым постоянным величинам. Например, одна из теорем П,Л.Чебышева формулируется так: "При неограниченном увеличении числа независимых испытаний fL среднее арифметическое свободных от систематических ошибок и равноточных результатов наблюдений X-_L случайной вели-f чины X , имеющих конечную дисперсию DCx] , сходится по вероятности к матема­тическому ожиданию М[Х] этой случайной величины.

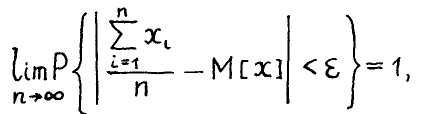
где £, — сколь угодно малая положительная величина.

Теорема Бернудли формулируется так: "При неограниченном увеличении числа не­ зависимых испытаний в одних и тех же условиях частота г (А) наступления слу- | чайного события А сходится по вероятности к его вероятности Р ", т.е. >

Поэтому, для того чтобы получить вероятность какого—либо события, например, i вероятности состояний системы массового обслуживания Р(0), Р(1),..., Р(К) вы-| числяют частоты Р =<п /п. для одной реализации. Далее проводят подобные вычис- !

ления для числа реализаций равного, например, ft = 1000. Результаты осредняют, и ! этим самым, с некоторым приближением получают искомые вероятности состояний си­стемы. На основании вычисленных вероятностей Pq , Р* _;Р* , ,., Р^ ,... , Р^

вычисляют математическое ожидание числа занятых каналов М СК], математичес­кое ожидание длины очереди М *[S] » среднее время пребывания в очереди ^*ср.ожид ^{и д}РУ^гие характеристики.

§ 23. Алгоритм для моделирования случайных величин, распределенных по показательному закону

Как было показано выше (§18), промежутки времени между двумя заявками на обслуживание, например, промежутки времени между двумя автомобилями, прибываю­щими на станцию технического обслуживания (так же, как и время обслуживания ука­занных заявок), распределено по показательному закону

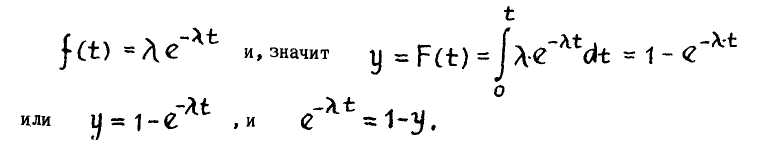
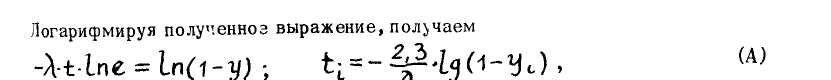
где yi — случайные числа, равномерно распределенные в интервале [ 0,1] и стохасти­чески независимые.

Таким образом, выражение (А) представляет собой алгоритм для моделирования случайных величин, распределенных по показательному закону.

Значения у -_ь обычно получают из таблицы равномерно распределенных случайных чисел. Для иллюстрации в табл. 12 дан фрагмент из указанной таблицы.

Таблица 12. Фрагмент из таблицы равномерно распределенных случайных чисел

27	76	74	35	84	85	30	18	89	77	29	49	06	97	14
03	54	51	43	38	54	06	61	52	43	17	72	46	67	33
80	21	73	62	92	98	52	52	43	35	24	43	22	48	96
10	87	56	20	04	90	30	16	11	05	57	41	10	63	68
54	12	75	73	26	26	62	91	90	87	24	47	28	87	78

Примечание к табл. 12. Все значения цифр, приведенных в табл. 12, меньше едини­цы, поэтому при пользовании таблицей впереди надо ставить нуль. Например, первое число составляет 0,27 и т.д.