Ю.В.Завадский

РЕШЕНИЕ ЗАДАЧ АВТОМОБИЛЬНОГО ТРАНСПОРТА С ПОМОШЫО МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Настоящее учебное пособие предназначается для слушателей факультета повышения квалификации преподавателей высших учебных заведений при Московском автомобильно—дорожном институте.

Оно отвечает программе обучения по курсу: "Специальные главы прикладной математики", содержит минимум теоретических сведений по "исследованию операций" - математической науке, применяемой для решения широкого класса задач и в том числе для анализа функционирования автомобильно—дорожных средств и систем.

В пособии даны порядок и методология решения задач по оптимальному управлению процессами, имеющими место в автомо­бильно-дорожной практике, содержится значительное число при­меров, иллюстрирующих излагаемые методы решения задач.

Материал пособия рассчитан на слушателей ФПК, впервые изу­чающих математический аппарат теории исследования операций с целью пос недующего его применения в их учебной и научно-иссле­довательской деятельности по месту основной работы.

ПРЕДИСЛОВИЕ

Настоящее пособие представляет собой краткий конспект лекций, прочитанных автором в 1978—79 гг. слушателям факультета повышения квалификации преподавате­лей высших учебных заведений при Московском автомобильно—дорожном институте.

В пособии кратко, применительно к различным техническим и экономическим задачам, возникающим при исследовании эффективности функционирования автомобильно— дорожных средств и систем, рассматриваются основные положения бурно развиваю­щейся в настоящее время математической науки — исследования операций.

В соответствии с учебной программой ФПК в пособии рассматриваются:

~ общие методологические вопросы и основные положения исследования операций,

• спектр математических моделей, применяемых для определения оптимальных решений по управлению исследуемыми процессами,

• порядок определения оптимальных решений для условий, когда математические модели задаются в виде уравнений регрессии или в виде статистических таблиц,

• основные положения случайных процессов, в том числе марковских случайных процессов,

• теория массового обслуживания,

• метод статистического моделирования и его применение для решения задач автомобильно— дорожной практики,

• основные положения линейного программирования и его применение для выбора такого способа организации действий, при котором критерий эффективности операции был бы максимальным,

• порядок экспертных оценок весов критериев применяемых при решении задач ав— томобильно—дорожной практики.

Пользуясь случаем, автор выражает глубокую благодарность доктору техн.наук, проф. Кодолову И.М., беседы с которым и его указания позволили автору написать на­стоящее пособие. Автор выражает также благодарность рецензенту — канд.техн.наук, доц. Колиниченко Б.А., просмотревшему рукопись и сделавшему ряд ценных замеча­ний.

ВВЕДЕНИЕ

В настоящее время можно считать общеизвестным, что проблема оптимизации р<*~ шений является одной из центрадьных в науке, технике и экономике.

Происходящая научно—техническая революция поставила перед инженерами, препо— давателями вузов, экономистами и учеными всех специальностей требование уметь ставить и решать задачи по оптимальному управлению процессами в той области, в которой они рабошют.

В своих докладах на XXIV и XXV съездах КПСС Л.И.Брежнев поставил перед со­ветским народом одну из важнейших задач — задачу дальнейшего совершенствования управления всеми отраслями народного хозяйства страны. Очевидно, чтобы управлять, необходимо уметь количественно оценить техническую и экономическую эффектив­ность различных решений, и на основе этого выбрать из них оптимальное.

При решении этой задачи важное значение приобрела прикладная математика, в особенности, одна из ее главных частей, называемая "ис с ле дование м опер аци и"

Исследование операций представляет собой комплекс научных методов, позволяющих решать задачи по эффективному управлению различными процессами. По определению академика Л.В.Канторовича,исследование операций — это область науки, изучающая вопросы выбора решений по организации и управлению целенаправленными процесса­ми (операциями).

п„„„„„„„ „„,_raeublp метоАами МСОДЭДоваиия операций, являются следствием функционирования системы некоторого числа взаимосвязанных и взаимодействующих эле­ментов.

Характерной особенностью исследования операций, т.е. исследования процессов, отвечающих заданным системам, как будет показано ниже, является так называемый системный подход, сущность которого состоит в том, что при решении любой из проб­лем необходимо исходить из положений диалектического материализма, согласно ко­торому все связано, едино и взаимообусловлено.

Среди систем различают статические и динамические системы. Статические системы - это системы,не развивающиеся во времени. Динамические системы -это системы,развивающиеся во времени. Обычно под динамической системой подразу­мевают иерархически организованную и целенаправленно функционирующую совокуп­ность большого числа связанных и взаимодействующих между собой элементов, объектов, агрегатов, подсистем, организаций и т.п. В общем случае система характе­ризуется следующими признаками:

• взаимодействует со средой и другими системами, как единое целое;

• состоит из подсистем более низкого ранга;

• является подсистемой для систем более высокого ранга;

• сохраняет общую структуру взаимодействия элементов при изменении внешних условий и внутреннего состояния.

Системы и протекающие в них процессы могут быть управляемыми и неуправляе­мыми. Примером неуправляемой системы может служить галактика, состоящая из множества звезд с движущимися вокруг них и развивающимися во времени цланетами.

Примером управляемых систем могут служить системы, созданные и создаваемые человеком для достижения определенной цели. Так, например, система автомобильно­го транспорта какого—либо города имеет своей целью удовлетворение потребностей общества в подвозе продуктов питания, доставке сырья на предприятия, транспорти­ровке готовой продукции потребителям, обеспечение перевозки пассажиров итл. Ука­занная система создана человеком, им управляется, непрерывно развивается во вре­мени и совершенствуется.

Системы и отвечающие им процессы, могут быть детерминированными и стохасти­ческими. Детерминированными — называются такие системы, для которых ин­формация об их состоянии и поведении на некотором отрезке времени позволяет одно­значно описать ее поведение в экстраполируемом интервале времени. Стохасти­ческими — называются такие системы, для которых информация об их состоянии и поведении на некотором отрезке времени не позволяет однозначно описать их поведе­ние в экстраполируемом отрезке времени.

При исследовании функционирования автомобильно—дорожных средств и систем (автомобилей, дорожно-строительных машин, строительстве дорог, дорожных соору­жений и тл.) приходится сталкиваться, главным образом, со сложными стохастически­ми системами, динамическими по своему характеру. Это обусловливается целым рядом причин, например, изменяющимися во времени различными условиями эксплуатации и обслуживания машин; несовершенством и различным качеством диагностики их со­стояния; неодинаковым качеством ремонта; изменением факторов внешней среды, например, чередованием времен года, погоды, состояний дорог, загрузки машин и т.п. Поэтому оценка состояния, прогноз на будущее время и определение оптимального управления для стохастических систем производится с позиций системного анализа с помощью различных разделов прикладной математики.

В качестве примера, иллюстрирующего необходимость применения системного анализа, можно, например, указать на систему строительства и эксплуатации автомобильных дорог заданной области или заданной республики, включающую:

• подсистему или сеть разработки нерудных материалов (карьеры по добыче песка, гравия, щебня и т.п.);

• подсистему или сеть цементно-бетонных и битумных предприятий;

• подсистему и сеть предприятий, производящую дорожное оборудование, в частности, строящую заправочные станции, ремонтные мастерские, устанавливающую дорожные знаки и оборудование для освещения дорог;

• подсистему цли сеть эксплуатации, ремонта существующих в настоящее время дорог и тл.

Каждая из перечисленных систем стремится выпускать как можно больше про­дукции, при этом по возможности одной номенклатуры, так как это снижает затраты на переналадку оборудования и обеспечивает перевыполнение цчана. Очевидно, что если это стремление не будет обосновано с позиций системного анализа, то это мо­жет привести к затовариванию или дефициту отдельных видов продукции на складах, например, к затовариванию цемента, битума и нехватки дорожного оборудования и тл. Финансовый же отдел всей системы, стремясь уложиться в запланированный бюджет средств, заинтересован в уменьшении запасов на складах, с тем, чтобы не было омерт­вления капитала.

Кроме рассмотренного, можно привести подобные примеры из других областей человеческой деятельности, где для решения з^дач также должен применяться систем­ный подход.

Как видим, требования у различных подсистем (подразделений), составляющих си­стему, различны и зачастую противоречивы. Это значит, что при решении любой про­блемы, в соответствии с требованиями системного анализа, необходимо оценить, как указанное решение скажется на функционировании всей системы в целом. Иначе го­воря, все проблемы надо решать одновременно и во взаимосвязи. Для этого надо ус­тановить связи и зависимости, характеризующие функционирование системы, опреде­лить накладываемые ограничения, выбрать соответствующие критерии и оценить функционирование системы в целом.

Заметим также, что решение задач исследования операций может производиться с позиций микро и макро подхода. Микроподход сводится к описанию функциониро­вания отдельных элементов (ячеек) из совокупности которых состоит вся система. При макроподходе сложная система рассматривается как черный ящик, т.е. исследуется ее функционирование в целом.

Глава I.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ

§ 1. Общие сведения

Как уже отмечалось выше, исследование операций — это методология или комп­лекс научных методов, с помощью которых могут решаться самые сложные современ­ные задачи техники, экономики и науки. Исследование операций — это часть киберне­тики, которая занимается вопросами организации управления.

Операцией — называют любое мероприятие, или систему действий, объединенных единым замыслом и направленным к достижению определенной цели.

Типовыми задачами исследования операций, например, являются:

• задача оптимального использования парка автомобилей или парка дорожно­ строительных машин данного района или города;

• задача оптимальной организации диагностики, технического обслуживания и ре­ монта автомобилей и дорожно—строительных машин;

• задача оптимального распределения подвижного состава по различным маршру­ там и различным объектам с целью выполнения заданного плана работ;

• задача оптимальной организации систем массового обслуживания, например, вы­ бора оптимального количества ремонтных постов и числа ремонтных бригад на стан­ ции технического обслуживания автомобилей;

• задача оптимального проектирования и строительства новых дорог, мостов, аэропортов и др. сооружений и тл.

Эффективность .операции — это степень ее приспособленности и выполнения постав­ленных перед ней задач, т.е. степень соответствия своему назначению.

Критери ем эффективности операций называется численный параметр или пока­затель, с помощью которого оценивается эффективность операции. Выбор критерия операции зависит от характера и цели операции. В качестве критерия эффективности может применяться вероятность какого—либо события Р(А) или среднее значение (математическое ожидание) случайной величины М (х).

Приведем несколько примеров критериев эффективности операций. Например, при оценке технического уровня дорожно—строительных машин в качестве критериев мо­гут служить: производительность, надежность, энергоемкость, ремонтопригодность, технологичность, показатель технической эстетики и др.

При оценке качества товаров массового потребления, например, одежды, показа­телями эффективности могут служить: соответствие моде, прочность, соответствие изделия форме человека и т.п.

При оценке качества учебного процесса со студентами Московского автомобильно— дорожного института показателями служат марксистско-ленинское мировоззрение и идейно—политический уровень студентов, а также знания и навыки в применении ос­новных разделов прикладной математики и электронно-вычислительных машин для решения инженерных и экономических задач, изучаемых студентами на специальных кафедрах института. Аналогично выбираются критерии эффективности при решении задач другого характера.

§ 2. Этапы операционного исследования

Исследование любой операции состоит из следующих этапов:

• постановка задачи с точки зрения заказчика;

• выбор математической модели;

• составление алгоритма для избранной математической модели;

• проверка математической модели на адекватность;

• реализация решения на практике. Рассмотрим последовательно каждый из этапов.

1. Постановка задачи

Постановка задачи — это важный этап операционного исследования. Первоначаль­но задачу формируют словесно с точки зрения заказчика. На этом этапе уясняются условия и ограничения, которые необходимо учитывать при решении задачи, а также производится качественный анализ исследуемого явления или процесса. В некоторых случаях для уяснения задачи могут производиться статистические наблюдения, т.е. сбор информации о процессе, подлежащем операционному исследованию. Собирается информация, характеризующая работу системы за прошлые периоды и в настоящее время. Информация об исследуемой системе может поступать в виде количественных показателей, т.е. в виде цифр, сигналов, сводок, требований и тд. На этапе постанов­ки задачи выясняется также вопрос о разрешимости поставленной задачи, т.е. произ­водится исследование принципиальной возможности решения задачи.

2. Выбор математической модели

После уяснения задачи и выяснения вопроса о ее разрешимости приступают к вы­бору вида математической модели, с помощью которой предполагается описывать изу­чаемое явление.

Сложность и многообразие процессов функционирования реальных систем не поз­воляет строить для них абсолютно адекватные математические модели.

Поэтому при составлении математических моделей отбрасывают все второстепен­ные факторы и оставляют лишь главные, определяющие факторы. Это значит, что математическая модель— это аналог реального явления, охватывающего лишь его основные свойства.

Математические модели являются основой прогнозирования, и, следовательно, яв­ляются основой планирования и оптимального управления исследуемым процессом.

В зависимости от условий и характера решаемых задач могут применяться различ­ные виды математических моделей и многочисленные методы и приемы моделирова­ния. Обычно различают физическое и математическое моделирование. На рис. 1 дан краткий спектр математических моделей, которые могут применяться при решении задач исследования операций.

В самом общем виде математическая модель представляет собой зависимость критерия (или критериев) эффективности операции от внешних неуправляемых факторов -♦ -» —>

У , от внутренней структуры системы £ ^{и от} принятого решения V по уп­равлению исследуемым процессам

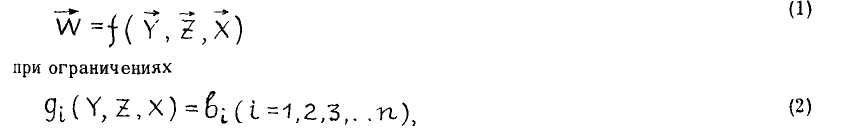
где W — критерий эффективности операции, параметр оптимизации, целевая функ— _» ция и т.п.;

Y — вектор внешних неуправляемых факторов системы (природа); Z — вектор внутренних параметров структуры системы;

X — вектор управляемых факторов системы (вектор принимаемых решений); di~ Функция ограничений по L—той переменной;

Ьь — величина ограничений по t-той переменной (так называемые дисциплини­рующие условия).

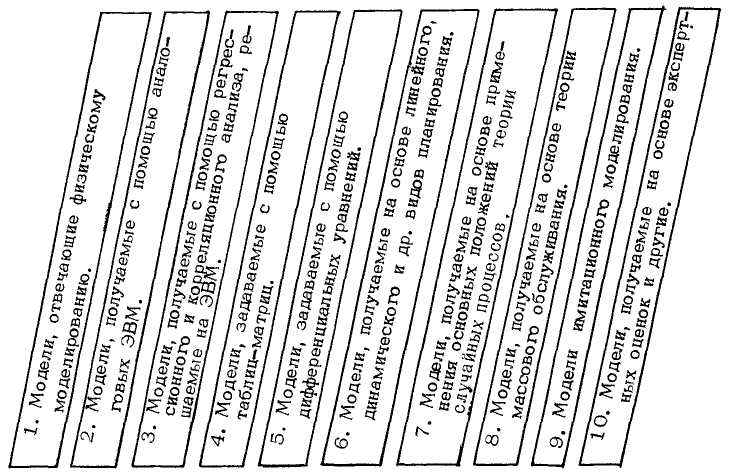
Рис. 1. Спектр математических моделей, применяемых при решении задач исследования операций

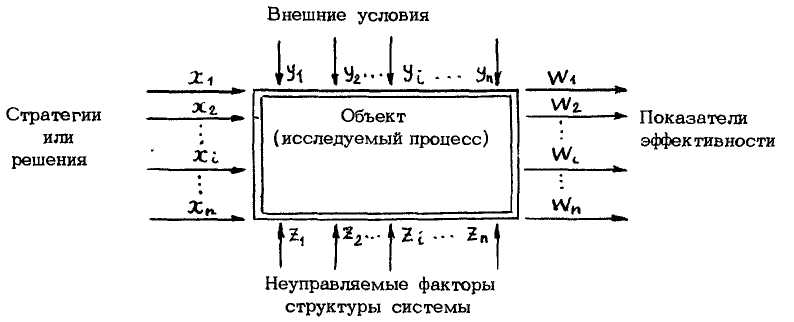
Внешние условия Y — представляют собой природу, т.е. объективную реальность, на фоне которой происходит функционирование системы. Например, время года, время суток, географическое положение объекта исследования, спрос, предложение и т.п. Постепенное изменение внешних условий называют дрейфом системы.

Неуправляемой частью структуры системы 2. , например, при решении авто — транспортными объединениями задач по транспортировке пассажиров, доставке про­дуктов питания, подвозе предприятиям сырья, необходимого для нормального течения производственного процесса и при решении других подобных задач, является качество автомобилей сегодняшнего дня (например, их грузоподъемность, скорость движения и т.п.), качество горюче—смазочных материалов и т д., т.е. такие факторы, которые не могут быть измзнены в процессе решения задачи сегодняшнего дня.

Вместе с тем, улучшение качества продукции, и, следовательно, улучшение качества автомобилей, качества горюче—смазочных материалов и тл. является важнейшей

Рис. 2. Схематическое изображение объекта исследования

При исследовании сложных технических и экономических систем возникает ряд трудностей, обусловливаемых следующими обстоятельствами¹:

• некоторые параметры внешней среды не могут быть измерены в силу неполной информации. Например, при анализе функционирования автомобильно—транспортной системы не всегда удается с прогнозом на будущее оценить качество будущих дорог, качество обслуживания, на,личие необходимых запасных частей и т.п. Неопределен­ ность в оценке состояния внешней среды для текущего момента времени создает еще большую неопределенность в оценке ее будущего состояния. Кроме того, параметры внешней среды в процессе функционирования системы могут меняться непредсказуе­ мым образом;

• численные параметры структуры системы оцениваются, как правило, с ошибка­ ми, обусловливающимися "шумами" измерительных средств и внешними помехами;

• часто системы обладают переменной (скользящей) структурой. Например, кон­ струкция автомобилей претерпевает непрерывные изменения: бензиновый двигатель может быть заменен газогенераторным или электрическим» а последний в свою очередь может быть заменен турбореактивным двигателем и т.п. Подобные изменения могут также происходить в подвеске, в конструкции кузова и в других агрегатах;

• наконец, эффективность функционирования технических и экономических сис­ тем, как правило, характеризуется иерархией показателей.

Показатели высшей ступени зависят от показателей более низкой ступени, а по­следние в свою очередь зависят от показателей еще более низкой ступени иерархии. Все выше перечисленные особенности усложняют решение задачи по исследованию сложной системы.

При исследовании сложных систем задачи могут быть_разделены_ на два вида:

1. задачи анализа, когда при заданных значениях Y , 2 X определя­ ется эффективность функционирования системы, W jpM. формулу 1);

2. задачи синтеза, когда^при заданных Y , Z и W определяется век­ тор оптимальной стратегии X »или когда при заданных значениях у X ^и \д/ определяется вектор оптимальной структуры системы

3. Составление алгоритма для избранной математической модели

После выбора вида математической модели и формализации исследуемого про­цесса заключающейся в отбрасывании всех второстепенных факторов, модель пред­ставляют в виде уравнений, графиков, схем и тл. Указанную формализованную мате­матическую модель называют алгоритмом процесса. Решение задачи с помошью по­дучаемого алгоритма производится, как правило, с помощью ЭВМ. Для этого получен­ный алгоритм представляют в виде операторной блок—схемы. Да,лее, на одном из ма­шинных языков (ДЛГОЛ, ФОРТРАН и т л.) составляется программа для решения зада­чи на ЭВМ.

4. Проверка математической модели на адекватность

Оценка математической модели на адекватность является весьма важной задачей. Эта проблема является достаточно сложной, так как она связана с многими логичес­кими, практическими и статистическими вопросами. В зависимости от условий провер­ка модели на адекватность может производиться, например, с помощью следующих способов:

• сличением полученных с помощью модели выходных данных с аналогичными дан­ ными, полученными на практике за прошлые периоды времени, если они имеются (практика—критерий истины);

• проверка адекватности статистическими методами, например, с помощью кри­ териев Фишера, Сьюдента и тл.

В случае несогласованности данных производится корректировка модели.

5. Реализация решения на практике

После составления математической модели, проверки ее на адекватность и ее кор­ректировки приступают к решению поставленной задачи. Результаты решения докла­дываются заказчику. Опыт показывает, что при решении операционной задачи на ос­нове хорошо подобранной математической модели получают значительный выигрыш в эффективности функционирования исследуемой системы.