§ 3. Основы оптимизации

Экстремальные методы. В практике эксплуатации автомоби­ лей и дорог (системы автомобиль-дорога) встречается ряд задач, в которых необходимо определить максимальные или минимальные значения тех или иных показателей или парамет­ ров. Известный математик Леонардо Эйлер считал, что в «мире не происходит ничего, в чем не был бы виден смысл какого-ни­ будь максимума или минимума». Это высказывание особенно подчеркивает важность экстремальных (от лат. extremum - крайнее) методов оптимизации. К числу таких задач можно отнести задачи по определению максимальной ^водитель ности автомобилей, минимальной себестоимости перевозки гру зов или пассажиров, минимального расхода топлива, макси­ мального пробега автомобиля до капитального ремонта, макси мальной пропускной способности дороги и т. д. _{ппнмрня}.

Известно, что для решения подобных задач широко примени ется дифференциальное исчисление. Имея функцию одной пере­меннойV=/W, ставим перед собой цель найти максимальное или минимальное значение величины у при каком-то наиболее экономичном значении x_SK. Решив эту задачу, получаем зави­симость изменения х_эк от других параметров, ^к°^тоР«е можно изменять по своему усмотрению и таким образом осуществлять управление данной операцией.

Если функция у = f(x) непрерывна и при значении аргумен­та Хэк имеет, например, максимум (рис. 13, а), то при увеличе­нии аргумента до значения х_ш функция растет, после х_эк — падает. Если функция имеет минимум (рис. 13, о), то, наоборот, сначала функция падает, а затем после х_эк растет.

Для значений аргумента, меньших х_эк (имеющих максимум), производная функция будет положительной, а для значений, больших Хэк — отрицательной. Вторая производная при этом меньше нуля, т. е. у"(х_эк)<0. Для вогнутой кривой, наоборот,

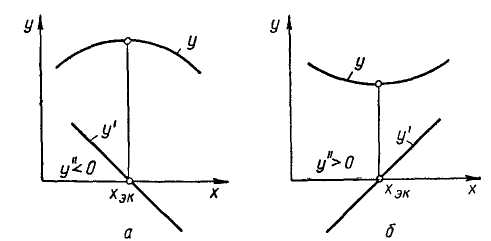
Рис. 13. Изменение функций и их производных.

для значений аргумента, меньших х_эк, производная будет отри­цательной, а для больших — положительной, вторая производная больше нуля г/"(#эк)>0. Из сказанного выше вытекает правило: если найдено такое х_зк, при котором /' (х_ж) = 0, /" (х_эк) < 0, то функция имеет максимум при х = *_эк. Если найдено такое х«, при котором /' (хэк) == 0 и /" (лгэк) > 0, то при х — х_ш функция имеет минимум.

Если окажется, что вторая производная равна нулю, надо определять третью, а то и четвертую производную. Дифферен­цирование производится до тех пор, пока производная не ока­жется положительной или отрицательной. Существует такое правило: если первая, третья и т. д. до некоторой производной нечетного порядка равны нулю, а следующая производная чет­ного порядка положительная, функция имеет минимум. Если она отрицательная,— функция имеет максимум.

Если есть функции двух переменных у — f{x\, x₂), необходимо найти производные у' (х\) и у'(х^, приравнять их к нулю, затем совместно решить уравнения у' (х\) — О и у' (х₂) = 0. Полученные значения Х\ и jc₂ будут соответствовать максимуму или минимуму функции у.

Рассмотрим примеры определения максимума и минимума.

Пример 1. Автомобили определенной марки (длины) движутся по дороге (в одном направлении) с коэффициентом сцепления колеса и дороги <р. Требу ется выбрать такой режим движения автомобилей (скорость движения и рас

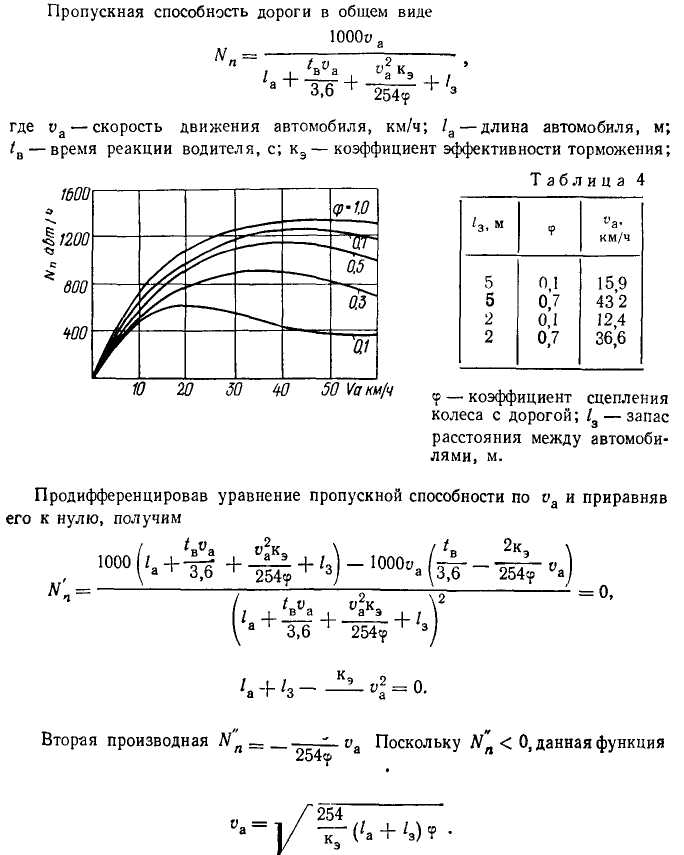
Рис. 14. Зависимость пропускной способности дороги от скорости ав­томобиля и коэффициента сцепления.

или в упрощенном виде

254?

2к.

имеет максимум. Отсюда

стояния между автомобилями), чтобы пропускная способность дороги была наибольшей.

При определенных значениях к_э, /_а и /₃ скорость о_а пропорциональна V<f-В табл. 4 приведены результаты расчетов скоростей движения, которым соответствует максимальная пропускная способность дороги, при к_э = 1,2; /_а = = 7 м. Из таблицы видно, что при увеличении <р до 0,7 и при /₃ = 5 м ско­рость возрастает до 43,2 км/ч. При уменьшении /₃ до 2 м и при ер = 0,1 скорость снизится до 12,4 км/ч.

Ыа рис. 14 представлены кривые изменения пропускной спо­собности дорог в зависимости от коэффициента сцепления и

скорости. В зависимости от скорости <р максимальная пропуск­ная способность снижается примерно в два раза.

Линейное и нелинейное программирование. Задачи линейно-го и.лшшщшного программирования относятся к экстремальным задачам со многими переменными. Линейными задачи назы­ваются потому, что искомые неизвестные входят в уравнения в первой степени. Экстремальными задачами считаются такие, решение которых позволяет выбрать план действий (програм­му), при котором достигается поставленная цель с наименьши­ми затратами или при заданных затратах достигается наилуч­ший результат. Получаем оптимальное решение, т. е. такое, при котором величина определенного показателя (критерия) явля­ется минимальной или максимальной. Таким образом, задачи линейного программирования являются частными случаями оптимизации, при которых рассматривается целевая линейная функция- вида

Нелинейное программирование делится на выпуклое (вниз) и невыпуклое. В первом случае локальный экстремум совпадает с глобальным (абсолютным). Такое программирование поэтому и называют одноэкстремальным. При невыпуклом программи­ровании локальный экстремум достигается в большом количе­стве точек (многоэкстремальная задача).

Наиболее разработанной частью нелинейного программирова­ния является квадратичное, которое находит широкое применение в различных областях науки и техники При этом оптимизируе-

мая функция имеет квадратичную формулу (или многочлен). В качестве примера выпуклую квадратичную функцию представим в виде W — а\Х\ + а₂х\ + йз*1*2 + сцх\ при ограничениях Х\ + + Х2 < Ъ\\ х\ > 0, хг > 0. Эта задача может быть решена методом последовательных приближений.

На автомобильном транспорте широко применяются задачи линейного программирования (транспортные задачи), позволя­ющие достаточно быстро и точно находить из большого числа наиболее выгодные варианты перевозок грузов, использования

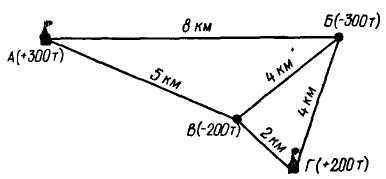
Рис. 15 Простейшая модель перевозок.

ресурсов и т. д. При ре­шении задач линейного программирования преж­де всего необходимо чет­ко сформулировать цели (критерии) управляемой системы. Далее количест­венно формируем систему ограничений по ресурсам. После определения целе-i вой функции и описания

системы ограничений приступаем к нахождению оптимального решения.

Поскольку в транспортных задачах линейного программиро­вания число неизвестных больше числа уравнений, аналитиче­ское решение их практически невозможно. Часто приходится рассматривать значительное количество вариантов перевозок при наличии нескольких отправителей и получателей груза. Пренебрегать математическими методами оптимизации нельзя даже при решении самых простых задач. Для примера рассмот­рим простейшую задачу планирования перевозок грузов. Из грузоотправляющих пунктов А и Г перевозится груз в грузопо-лучающие пункты В и Б (рис. 15). Из пункта А может быть перевезено 300 т, из пункта Г — 200 т. Расстояния перевозок указаны на рис. 15. Необходимо так спланировать перевозки, чтобы общий объем транспортной работы в тонно-километрах или среднее расстояние груженой ездки было минимальным.

На первый взгляд кажется, что наиболее целесообразно весь груз из пункта А доставлять в пункт Б, а из пункта Г — в пункт В. Общий объем транспортной работы при этом составит 300-8+200-2 = 2800 т-км. На самом деле близким к оптималь­ному варианту перевозок будет следующий: из пункта А в пункт В перевозится 200 т и в пункт Б —100 т. Из пункта Г перево­зится 200 т в пункт Б. Распределение груза осуществлено с уче­том наименьших расстояний перевозок. В этом случае транс­портная работа будет минимальной: 200-5+100-8+200-4 = = 2600 т • км. Среднее расстояние перевозок одной тонны груза в первом варианте составляет 5,6 км (2800:500), во втором — 5,2 rm (2600:500). Таким образом, при грамотном подходе к

решению даже этой простейшей задачи можно добиться сниже­ния объема транспортной работы на 6%.

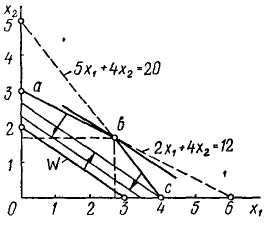
Рис. 16. Геометрическая ин­терпретация задачи с дву­мя переменными.

Для решения сравнительно простых задач, когда результат зависит от двух, максимум трех переменных, применяются гра­фические методы. При трех неизвестных графическое изобра­жение можно выполнить в трех измерениях. В случае значи­тельного числа ограничений решение задач с тремя неизвест­ными теряет практический смысл. Общий геометрический смысл задачи линейного программирования заключается в отыскании на прямой или многограннике точки, которая наиболее (или наименее) уклонена от прямой или плоскости. При ре­шении подобных задач может быть различное количество ограничений, выраженных равенствами или не­равенствами вида

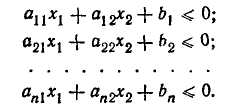
Линейная функция (стоимость перевозок) в случае двух переменных

Пусть, например, необходимо максимизировать функцию 10 xi + 15*2-> max при ограничениях

Графическое решение поставленной задачи показано на рис. 16. Стрелки направлены в сторону допустимых значений. Как видно из графика, область допустимых значений х\, X2 ограничена мно­гоугольником oabc. Множество точек этой области называется множеством решений. Данное множество является выпуклым, так как любой отрезок, соединяющий любые две точки Множе­ства, лежит внутри или проходит по границе многоугольника. В линейном программировании рассматриваются только выпук­лые множества. Экстремальными точками называются верши­ны о, а, Ь, с. Различные значения целевой функции показаны параллельными линиями. Экстремальная точка Ь, для которой х\ = ⁸/з и Хо = ⁵/з, соответствует оптимальному решению. Целе-

вая функция будет 10^-f 15*₂=-4- •

О

Не для всех случаев существует оптимальное решение. На* пример, если целевая функция имеет вид W — aiXi-\-a₂x₂ при ограничениях — an*i+fli2*2< b\ и ацХ\— «22*2 <^ &2, то, как видно из рис. 17, а, в этом случае не существует оптимального

мая функция имеет квадратичную формулу (или многочлен). В качестве примера выпуклую квадратичную функцию представим в виде W = а\Х\ + а₂х\ + аъХ\Х₂ + а\х\ при ограничениях х\ + + х₂ < Ь\\ х\ > 0, х₂ > 0. Эта задача может быть решена методом последовательных приближений.

На автомобильном транспорте широко применяются задачи линейного программирования (транспортные задачи), позволя­ющие достаточно быстро и точно находить из большого числа наиболее выгодные варианты перевозок грузов, использования

ресурсов и т. д. При ре- 8 к» б(-ЭООт) шении

задач линейного программирования преж­де всего необходимо чет­ко сформулировать цели (критерии) управляемой системы. Далее количест­венно формируем систему ограничений по ресурсам. После определения целе* вой функции и описания

системы ограничений приступаем к нахождению оптимального решения.

Поскольку в транспортных задачах линейного программиро­вания число неизвестных больше числа уравнений, аналитиче­ское решение их практически невозможно. Часто приходится рассматривать значительное количество вариантов перевозок при наличии нескольких отправителей и получателей груза. Пренебрегать математическими методами оптимизации нельзя даже при решении самых простых задач. Для примера рассмот­рим простейшую задачу планирования перевозок грузов. Из грузоотправляющих пунктов А и Г перевозится груз в грузопо-лучающие пункты В и Б (рис. 15). Из пункта А может быть перевезено 300 т, из пункта Г — 200 т. Расстояния перевозок указаны на рис. 15. Необходимо так спланировать перевозки, чтобы общий объем транспортной работы в тонно-километрах или среднее расстояние груженой ездки было минимальным.

На первый взгляд кажется, что наиболее целесообразно весь груз из пункта А доставлять в пункт Б, а из пункта Г — в пункт В. Общий объем транспортной работы при этом составит 300-8+200-2 = 2800 т-км. На самом деле близким к оптималь­ному варианту перевозок будет следующий: из пункта А в пункт В перевозится 200 т и в пункт Б — 100 т. Из пункта Г перево­зится 200 т в пункт Б. Распределение груза осуществлено с уче­том наименьших расстояний перевозок. В этом случае транс­портная работа будет минимальной: 200-5+100-8-f-200-4 = = 2600 т • км. Среднее расстояние перевозок одной тонны груза в первом варианте составляет 5,6 км (2800:500), во втором — 5,2 км (2600:500). Таким образом, при грамотном подходе к

решению даже этой простейшей задачи можно добиться сниже­ния объема транспортной работы на 6%.

Для решения сравнительно простых задач, когда результат зависит от двух, максимум трех переменных, применяются гра­фические методы. При трех неизвестных графическое изобра­жение можно выполнить в трех измерениях. В случае значи­тельного числа ограничений решение задач с тремя неизвест­ными теряет практический смысл. Общий геометрический смысл задачи линейного программирования заключается в отыскании на прямой или многограннике точки, которая наиболее (или наименее) уклонена от прямой или плоскости. При ре­шении подобных задач может быть различное количество ограничений, выраженных равенствами или не­равенствами вида

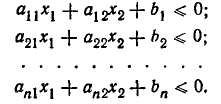
Линейная функция (стоимость перевозок) в случае двух переменных

Пусть, например, необходимо максимизировать функцию 10 xi + 15x2-> max при ограничениях

Графическое решение поставленной задачи показано на рис. 16. Стрелки направлены в сторону допустимых значений. Как видно из графика, область допустимых значений х\, х₂ ограничена мно­гоугольником oabc. Множество точек этой области называется множеством решений. Данное множество является выпуклым, так как любой отрезок, соединяющий любые две точки множе­ства, лежит внутри или проходит по границе многоугольника. В линейном программировании рассматриваются только выпук­лые множества. Экстремальными точками называются верши­ны о, а, Ь, с. Различные значения целевой функции показаны параллельными линиями. Экстремальная точка Ь, для которой *\ = ⁸/з и х₂ = ⁵/з, соответствует оптимальному решению. Целе-

Не для всех случаев существует оптимальное решение. На­пример, если целевая функция имеет вид W = а\Х\-\-а₂х₂ при ограничениях — а.пХ\-\-а\₂х₂ <С Ь\ и п2\Х\ — а₂₂х₂ < Ь₂, то, как видно из рис. 17, а, в этом случае не существует оптимального

решения. Экстремальная точка отсутствует. Она лежит в беско­нечности. На рис. 17,6, в показано графическое решение задач при наличии пяти ограничений для случая максимума и миниму­ма. Геометрическая интерпретация задач линейного программиро­вания с тремя неизвестными Х\, х%, х₃ показана на рис. 18.

X/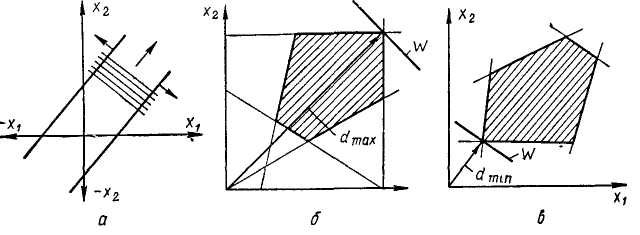

Рис. 17. Примеры графического решения задач.

Допустим, необходимо максимизировать выражение W = = а ]Л"! -f-a2*2+#3*3 при наличии многих ограничений вида flii *i + «(2X2 + 0(3*3 + b_t < 0. Решение задачи сводится к нахож­дению самой высокой точки выпуклого многогранника. Чтобы найти такую точку и решить линейную программу, требуется

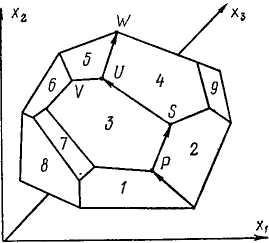
проверить все вершины по специаль­ному алгоритму, предложенному Д. Данцигом [13]. Этот универсаль­ный алгоритм, получивший название симплекс-метод, позволяет решать графически, а также с помощью таб­лиц сложные задачи со многими пе­ременными. Небольшие по объему задачи можно решать вручную.

Рис. 18 Геометрическая ин­терпретация задачи с тремя переменными.

Первый шаг решения сводится к нахождению какой-нибудь вершины многогранника. Допустим, этой вер­шиной является точка Р, образован­ная пересечением плоскостей 1, 2, 3. Далее (второй шаг) от точки Р осу­ществляем движение вдоль ребра, образованного пересечением плоскостей 1, 2, и определяем его подъем или снижение. Так же анализируем ребра, образованные плоскостями 2—3 и 3—1. Если на этих ребрах не происходит подъема, можно считать, что точ­ка Р является максимизирующей точкой. На третьем шаге ана­логичным образом находим вершину, образованную пересечени­ем плоскостей 2, 3, 4. Повторив все три перечисленных шага, оп­ределяем более высокую вершину U. Далее таким же образом устанавливается и самая высокая вершина многогранника W,

Общая методика решения задач линейного программиро­вания — последовательное улучшение вариантов. Составляем начальный план. Для сокращения объема расчетов он должен быть по возможности близким к оптимальному. Затем по опре­деленному алгоритму отыскиваем варианты лучше предыдущих. В конце концов находим оптимальный вариант.

Из специальной литературы известны такие методы решения задач линейного программирования: симплексный, распредели­тельный, метод потенциалов, методы разрешающих множителей и слагаемых и др. Универсальным методом, пригодным для решения разных типов задач, является симплексный метод. Однако он громоздкий и, как правило, требует применения ЭВМ. Другие методы проще, но пригодны для решения относительно простых задач. Для каждого типа задач обычно выбирается ют или иной метод решения. Наиболее простым методом линей­ного программирования является распределительный, имеющий несколько способов вычислений.

Существуют разные способы составления первоначального плана. Например, способ северо-западного угла, при котором распределение начинается с заполнения верхней левой (северо­западной) клетки таблицы. При этом расстояние перевозок не учитывают. Более совершенным способом распределения явля­ется такой, при котором сначала загружаются клетки таблицы с минимальным расстоянием. Так постепенно загружаются все клетки. Широко применяется метод, при котором выбирается наименьшее расстояние в каждой строке и по каждому столбцу. Загружаются прежде всего клетки с двумя отметками, а затем с одной.

Рассмотрим решение простой задачи (15 клеток) методом потенциалов.

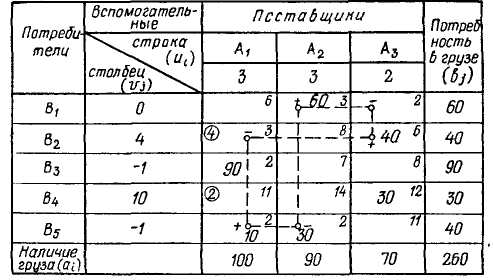
В табл. 5 с исходными данными дополнительно вводим вспо­могательную строку и столбец. В правых верхних углах клеток указано расстояние перевозок (км), пропорциональное стоимо­сти перевозок груза. Решение задачи можно условно разбить на четыре этапа.

1. Составление исходного плана или опорного решения. За­ писываем вес груза в клетки с наименьшим расстоянием по каждому столбцу. В клетке А\В₃ запишем 90 т, в А\Вь— осталь­ ные 10 т. Далее в клетке А₂В₅ — 30 т и в А₂В\— 60 т. В клет­ ках А3В2 и Л3В4 — 40 и 30 т соответственно.

2. Нахождение специальных цифровых индексов (потенциа­ лов). Индексы проставляем в клетках вспомогательной строки и столбца. В клетке пункта Si записываем нуль. В остальных клетках запись производится по такому правилу: величина рас­ стояния загруженной (базисной) клетки должна равняться сумме индексов вспомогательной строки и столбца. Например, в клетке A₂Bi 3 = 0+3, в клетке А₂В₅ 2=3 — 1, в клетке А\В_Ъ 2 = —1+3 и в клетке А\В_г 2 = 3—1. Чтобы найти все

индексы (потенциалы), необходимо, чтобы количество загру-> женных клеток равнялось (n-j-m — 1), где п — число столбцов, т — число строк. В нашем примере (п -f- т — 1) =3+5 — 1 =7, а фактически загружено 6 клеток. Если число загруженных кле* ток меньше, то их надо искусственно загрузить. Запишем 0 в клетке АгВ\. После этого могут быть определены все индексы.

Таблица 5

3. Проверка оптимальности. Для проверки оптимальности по­ лученного распределения отыскиваем среди незагруженных клеток такие, для которых сумма соответствующих индексов будет больше величины расстояния, указанного в этой клетке (и, -f u_t > /,/). Разность между суммой и расстоянием запиеываем в кружке в клетке. Эта разность — то дополнительное снижение пробега, которое можно получить на единицу груза, перемещенного в эту клетку.

4. Построение контуров. Выбираем незагруженную клетку с наибольшей цифрой, обведенной кружком. Для нее строится «контур» — замкнутая ломаная линия, состоящая из прямых горизонтальных и вертикальных отрезков, соединяющих эту клетку с другими загруженными клетками. После этого всем клеткам, где образуется прямой угол, попеременно присваиваем знак плюс или минус, в первоначально выбранной клетке ста­ вится минус. «Контур» может быть только один для данной выбранной незагруженной клетки. Он может иметь самые раз­ нообразные формы (рис. 19).

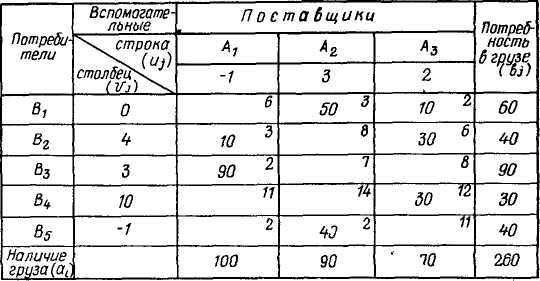
Далее из всех клеток со знаком плюс выбираем наименьшую цифру загрузки. Это число вычитаем из загрузки всех клеток со знаком плюс и прибавляем к загрузке всех клеток со знаком минус. При этом общая сумма в столбцах остается прежней, изменяется лишь распределение груза среди потребителей (табл. 6). С учетом новой таблицы повторяем все ранее описан­ные операции. Если распределение улучшить нельзя, оно счи* тается оптимальным.

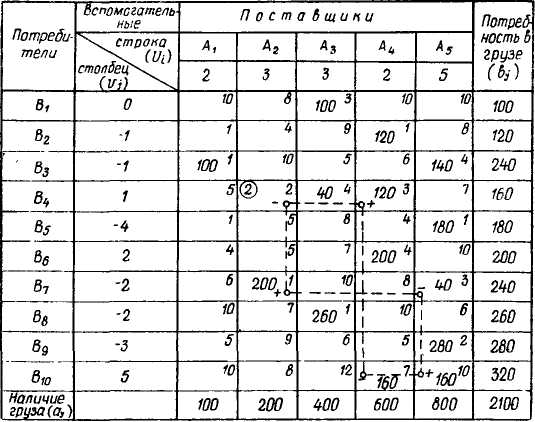
В рассматриваемом примере больше нет клеток, где рас­стояние было бы меньше суммы цифр в столбце и строке. Сле­довательно, получено оптимальное решение. На этом решение задачи заканчивается.

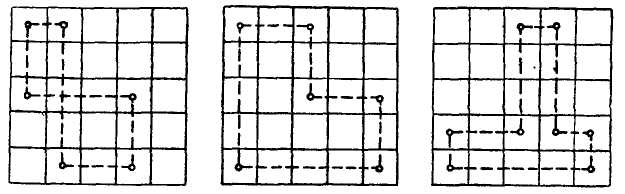
Рис. 19. Виды «контуров».

Сравним суммарную транспортную работу по предваритель­ному распределению груза с окончательным распределением. В первом случае транспортная работа равна 1040 т• км (60-3+40-6+90-2+30-12+10-2+30-2), во втором —970 т-кд* (50-3+10-2+10-3+30.6+90-2+30-12+40-2). Как видим, объ­ем транспортной работы вследствие снижения среднего расстоя­ния перевозок груза уменьшился на 7% (на 70 т • км).

Таблица б

Рассмотрим более подробно решение задач методом потенциа­лов. Обозначим через х_ч количество перевезенного груза, а через 1ц — расстояние перевозок. Пусть каждый отправитель (поставщик) груза A_t за перевозку единицы груза вносит еумму ы,, а каждый получатель (потребитель) — v, и эти взносы получает лицо, осу­ществляющее перевозки («перевозчик»). Сумма может быть как положительной, так и отрицательной (когда, например, «перевоз­чик» платит премию отправителю или получателю груза): ы, +

-\-v, = /,,(i =» 1, 2, ... т\ 1 = 1, 2, ... п). Величину /,-, назовем «пеевдоетоимостью» (мнимой втоимовтью) перевозки единицы груза

из пункта At в пункт В/. Стоимость (действительная) перевозки единицы груза из Л,- в В,- равна 1ц. Существует «теорема о пла­тежах», из которой следует, что для заданной совокупности

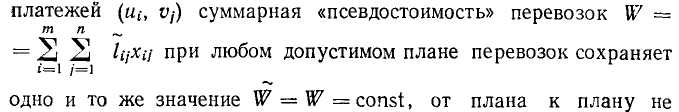
меняется и зависит только от запасов а,, заявок Ь\ и платежей

Ui И Vj.

Между «псевдостоимостью» и действительной стоимостью су­ществует определенная связь, которая вытекает из следующей

Таблица 7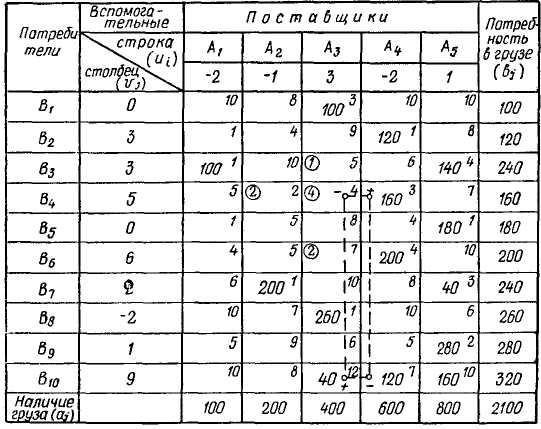

клеток (при х^ = 0) Ut + с,- = /,,• < 1ц, то план является опти­мальным и никакими способами улучшен быть не может. Другими словами, признаком оптимальности плана перевозок груза явля­ется выполнение двух условий: для всех базисных клеток 1_{] =

= /(/, для всех свободных клеток 1ц < /;_г Такой план называ­ется потенциальным, а соответствующие ему платежи ы₍ и Vj — потенциалы пунктов A_t и В,. Можно сказать, что всякий потен­циальный план является оптимальным.

Рассмотрим более сложный пример (на 50 клеток) решения транспортной задачи тем же методом потенциалов. Как и в рас­смотренном выше примере строим табл. 7 с исходными данными и добавляем вспомогательные строку ui и столбец v,-.

Далее (1-й этап) производим первоначальное распределение, которое' заключается в выборе клеток таблицы с минимальным расстоянием и загрузкой ее грузом, равным минимуму по строке. Определяем цифровые индексы (2-й этап) по правилу /,₇ = Vj + + «г и проставляем их в клетках вспомогательного столбца и строки.

Первый индекс, равный нулю, заносится в клетку вспомо­гательного столбца, которая соответствует первому пункту на­значения. Количество загруженных клеток в этом примере равна

Таблица в

14 (n-fm—1), поэтому необходимость в искусственной загруз­ке клеток отпала.

Для проверки оптимальности (3-й этап) в незагруженных клетках записываем положительные числа — разность между сум­мой соответствующих индексов и расстоянием (если о,- + м, — — 1ц < 0, план считается оптимальным; клетки, в которых v_t + + щ—1ц > 0, называются потенциальными). Эти числа обводим кружками (в клетке А₂В₄ — 2, /4₃В₄ — 4, Л₃В₆ — 2).

Для клетки с наибольшей цифрой {А₃В^) строим контур и по известному правилу производим перераспределение груза (табл. 8). Загрузку тех клеток, которые не отмечены знаком плюс и минус, переносим без изменения. Затем вновь отыски­ваем индексы в незагруженных клетках и определяем незагру­женные потенциальные клетки (в табл. 8 такой клеткой явля-

ется A₂Bi). Для нее вновь строим контур и производим пере­распределение груза (табл.9).

Таблица 9

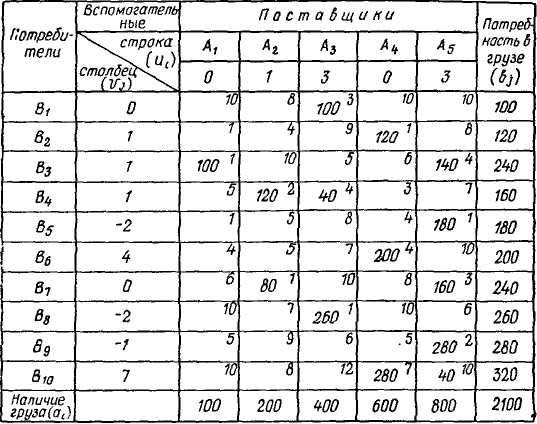
Для табл. 9 пытаемся снова определить индексы и потен­циальные клетки. Поскольку потенциальные клетки отсутству-< ют, полученное распределение считаем оптимальным.

Суммарная транспортная работа в первоначальном распре­делении составила 6600 т • км, среднее расстояние перевозок — 3,15 км. В окончательном варианте объем транспортной рабо­ты— 6200 т-км, среднее расстояние перевозок удалось снизить до 2,95 км (6%).

Если число загруженных клеток не (т+п— 1), a (m-fn), может быть два индекса в одном столбце. Чтобы исключить один из них, надо или перераспределить груз, или для одной из загруженных клеток построить контур, в который должны входить обе загруженные клетки столбца. Затем определяется алгебраическая сумма из расстояний всех клеток в вершинах построенного контура. В первой клетке при этом ставится знак плюс, а остальным поочередно присваиваются знаки минус и плюс. Если сумма положительная, в выбранной клетке оста­ется знак плюс, если отрицательная — минус. В остальных клет­ках поочередно проставляется то один, то другой знак. Если сумма равна нулю, в выбранной клетке можно ставить любой знак. В дальнейшем перераспределяется груз во всех клетках контура по описанному выше правилу. В результате такого перераспределения в данном столбце остается одна загружен­ная клетка и индекс устанавливается однозначно. В конце опе-

64

вариантов закрепления грузополучателей за грузоотправителя­ми), но и закрепления автохозяйств за грузовладельцами, выбора типа подвижного состава и распределения его по маршрутам, определения необходимого числа автомобилей, погрузочно-раз-грузочных механизмов и др.

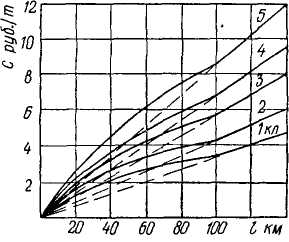
При выборе маршрутов перевозок критериями оптимально­сти считаются затраты на оплату перевозок по тарифам, себе­стоимость перевозок, пробег автомобиля и время доставки гру­за. Затраты на перевозки исчисляются в соответствии с дейст­вующими тарифами, которые учитывают расстояние перевозок, класс груза и частично дорожные условия.

До сих пор рассматривались транспортные задачи, в которых в качестве критерия взято рассто­яние перевозок. Это расстояние пропорционально стоимости пере­возок. Фактически критерием оп­тимальности была стоимость пе­ревозок, и мы стремились эту стоимость минимизировать.

Рис. 20. Изменение тарифной платы.

На рис. 20 показано изменение стоимости перевозки одной тонны данного груза в зависимости от расстояния (по прейску­ранту единых тарифов). При изменении расстояния от 1 до 100 км стоимость перевозок, например груза первого класса, изменяется от 0—25 до 3—40 руб. При расстоянии перевозок свыше 100 км тарифная плата составляет дополнительно 3,4 коп. за каждый километр. Из графика видно, что между тарифом и расстоянием линейная зависимость отсутствует. При решении задач линейного программирования необходимо учитывать от­сутствие линейной зависимости между стоимостью и расстоя­нием перевозок.

Методика решения транспортных задач по критерию време­ни практически ничем не отличается от изложенной. Оптималь­ным планом перевозок (х_ч) будет такой, при котором среднее время перевозок (нахождения груза в пути) минимально. В транспортную таблицу вместо расстояния перевозок 1ц про­ставляется время ti,. С помощью методов линейного програм­мирования можно решать и ряд других задач.

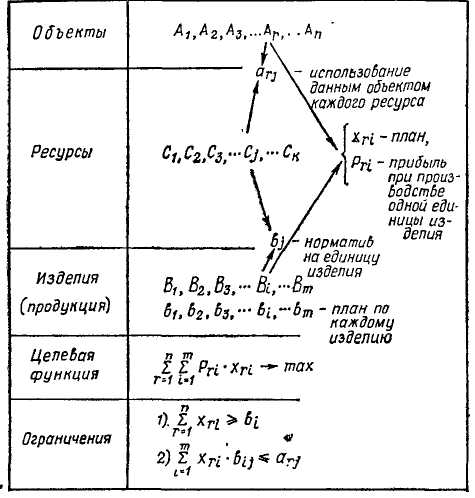
Рассмотрим общую математическую формулировку задачи линейного программирования [11, 15]. Пусть имеется п объектов Ль Аг, ... , А„ (заводов, цехов, автопредприятий), на которых производится т различных изделий В\. В₂, ..., В_т. Каждый объект располагает определенными ресурсами (станками, автомо­билями). По каждому изделию Б,- установлен директивный план Ь{, который должен быть выполнен всеми объектами.

Известен также норматив Ъц, необходимый для производства единицы г-го продукта по /-му ресурсу, и степень использования Данным объектом А, каждого ресурса С, = а_п (табл. 11).

Таблица 11

Необходимо составить планы x_ri выпуска изделий t-ro вида на r-и объекте, при осуществлении которых достигается макси­мально возможная прибыль Р_п от производства единицы изделия. Суммарная прибыль (целевая функция) определится как сумма прибылей на всех объектах при производстве запланированной продукции:

При нахождении оптимального и положительного плана (хн > 0) следует соблюдать два основных условия (ограничения):

выполнение директивного плана производства продукции fy

Число уравнений в задачах линейного программирования — (т + nk). Так, если необходимо найти оптимальное решение между 15 предприятиями (л = 15) по 30 видам изделий (т = 30) при 10 видах ресурсов (k = 10), общее число уравнений будет рав­няться т + nk = 30 + 15 • 10 = 180.

Общее число неизвестных устанавливается по формуле

{тп + т + kn) = п (т + к) + т = 15 (30 + 10) + 30 = 630.

Общее количество арифметических опера­ций N_o для выполнения одного симплексного преобразования при ре­шении задачи линейно­го программирования приближенно определя­ется как произведение числа уравнений на об­щее число неизвестных:

N₀^(m + n k) x Х(пт-\- kn -f- tri).

Рис. 21. Модель транспортной сети.

В рассматриваемом примере No =180 -630 = = 113 400. Практически необходимо выполнять сотни и тысячи симп­лексных преобразова­ний, в связи с чем об­щее количество ариф­метических операций

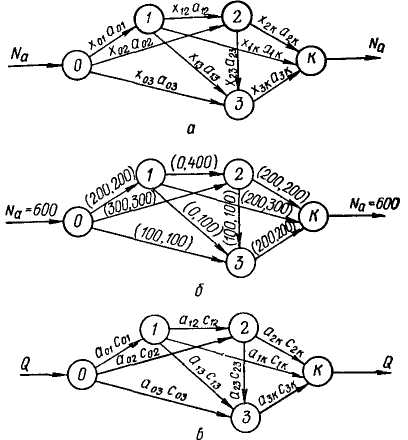
достигает миллионов и даже миллиардов арифметических опера­ций. По расчетам акад. В. М. Глушкова [11], при восьмичасовой активной работе (без выходных дней и отпуска) человек спосо­бен выполнить в год не более 10⁶ операций. Отсюда можно сде­лать вывод о трудоемкости задач линейного программирования. Многие практически важные задачи линейного программиро­вания сводятся к решению сетевых задач (автомобильные и железные дороги, трубопроводы, линии связи и т. д.). Пусть, например, по дорожной сети, представленной на рис. 21, а, не­обходимо пропустить наибольшее число автомобилей из пункта отправления О в пункт назначения К. Другими словами, необ­ходимо определить максимальный поток N_a. Узловые пункты (места прохода б одного пути на другой) обозначим цифрами. Направление потока автомобилей покажем стрелками. В этих сетях должно соблюдаться условие сохранения потока в про­межуточных пунктах: количество поступающих в данный узел автомобилей равняется выходящему из него числу автомобилей.

Используя пути с заданной пропускной способностью, требуется пропустить наибольшее число автомобилей, т. е. максимизировать поток автомобилей. Пусть хц — количество поступающих авто­мобилей из узлового пункта i в пункт /. Максимальный поток (верхнюю границу или пропускную способность) на каждом пути обозначим ац. На всех путях хц < ац.

Для каждого узлового пункта можно составить свое урав­нение. Задача линейного программирования сводится к макси­мизации N₃ при следующих ограничениях по пропускной спо­собности:

Задача о максимальном потоке может быть решена в общем случае с помощью симплекс-метода.

Оптимальные решения можно находить и более простыми методами. Обозначим второй цифрой на каждом пути (рис. 21,6) пропускную способность. Для каждого сечения (множе­ства путей, которые будучи удалены, делят сеть на две не свя­занные части) можно определить общую пропускную способ­ность. Для сечения 0—1, 0—2, 0—3 общая пропускная способ­ность 600 (200+300+100). Для сечений: 1—2, 1-К, 1—3, 0—2, 0—3— 1200; 0—3, 1—3, 1—К, 2—3 и 2-К —800; 2—К, 1—К и 3—К — 700. В соответствии с основной теоремой теории сетей максимальный поток из пункта 0 в пункт К равен минимальной пропускной способности среди всех сечений. Таким образом, максимальный поток будет равен 600. Распределение автомоби­лей вдоль каждого пути показано первыми цифрами.

С помощью сетевых задач можно решать и другие транспорт­ные задачи линейного программирования. Рассмотрим постановку задачи о потоке минимальной стоимости. Допустим, имеется такая дорожная (транспортная) сеть, по которой необходимо перевезти Q груза из пункта О в пункт К. На каждом пути

определенная стоимость перевозки одной тонны груза — Сц. Не­обходимо так спланировать перевозку, чтобы общая стоимость была минимальной. На каждом пути можно транспортировать хц тонн однородного груза. Ограничения по объемам перевозок обозначим ац. На рис. 21, в каждому пути соответствуют зна­чения ац и сц. В этой задаче необходимо минимизировать целе­вую функцию

Задачи о потоке минимальной стоимости можно решать с помощью универсального симплекс-метода или другими специ­альными методами.

Динамическое программирование. Задачи динамического программирования (планирования) относятся также к оптими­зационным, в которых рассматриваются и анализируются мно­гошаговые операции, развивающиеся во времени. На каждом «шаге» или «этапе» принимается определенное решение, от это­го зависит успех всех последующих этапов и операций в целом. С помощью динамического программирования осуществляется планирование управляемых процессов.

Примером одной из наиболее распространенных задач ука­занного типа является задача о коммивояжере, который ставит перед собой цель выбрать такой маршрут движения из началь­ного пункта в конечные, при котором бы ему удалось посетить их по одному разу и возвратиться в исходный пункт, преодолев минимально возможное суммарное расстояние. Расстояния меж­ду отдельными пунктами известны. Эту задачу можно решить

путем перебора и анализа всех возможных маршрутов. Рас­смотрение всего множества вариантов весьма трудоемко. Изве­стно, что количество перебираемых вариантов равно числу пере­становок из т элементов, т. е. произведению 1, 2, 3,..., т. На­пример, если автомобиль должен доставить груз со склада в 10 магазинов, то для выбора оптимального маршрута необхо­димо рассмотреть 10! вариантов маршрутов, т. е. 3 628 800 ва­риантов. В случае затраты 1 мин на оценку каждого маршрута потребуется около тридцати лет для решения этой задачи при работе одного человека. Задача значительно усложняется, если количество складов будет п. Тогда число вариантов определя­ется из выражения (/п!)^п. Задачи такого класса с трудом реша­ются даже при использовании современных ЭЦВМ.

С целью экономии времени применяются решения, близкие к оптимальным. Например, известны методы дискретной опти» мизации, получившие широкое распространение в «теории рас­писаний» (теории календарного планирования).

В общем виде задачи динамического программирования фор­мулируются следующим образом. Необходимо из множества до­пустимых возможных управлений м_доп найти такое, при котором данная система х переходит из начального состояния хо в ко­нечное Xk и показатель эффективности (целевая функция, «выиг­рыш») W (и) при этом обращается в максимум или минимум:

При решении задач динамичеекого программирования рас­сматриваются: управляемая система х, которая может менять свое состояние во времени; показатель эффективности, чиеленно выражающий желание достичь определенной цели; начальное хо и конечное состояния системы х-_л, ограниченные некоторыми

УСЛОВИЯМИ Ходог И ХД.ДОП.

Состояние управляемой системы х описывается определен­ным количеством параметров (скорость движения автомобиля, производственные затраты, численность машин и рабочих и т. д.). Эти параметры — фазовые координаты системы х. Со­стояние системы изображается точкой х с этими координатами в условном фазовом пространстве (или пространстве состоя­ния). При наличии одного параметра (например, скорость авто­мобиля) фазовое пространство будет одномерным (рис. 22, а, прямая линия), в случае двух параметров (например, скорость движения и расход топлива автомобиля) — двумерным (рис, 22, б), при трех параметрах — трехмерным (рис. 22, в).

Траектория перемещения точки х изображает процесс управ­ления. Пунктиром обозначены области возможных состояний системы. При решении задач динамического программирования процесс перемещения точки х из начальной области (точки) в конечную (точку) разбиваем на ряд последовательных шагов. Оптимизация пооизводится постепенно от шага к шагу, начиная

с последнего. При этом на каждом шаге находятся условные оптимальные управления и из множества решений выбирается одно.

Рассмотрим простой пример определения кратчайшего пути перемещения передвижной диагностической станции (ПДС) для установления технического состояния автомобилей в небольших автохозяйствах района. Методика решения подобной задачи приведена в работе [11].

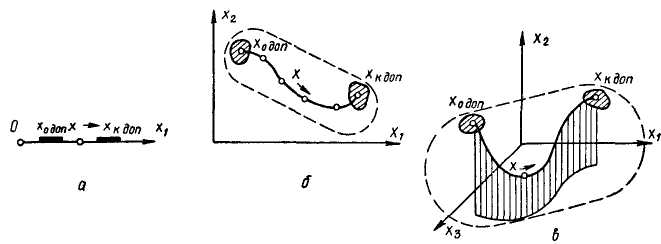
Рис. 22. Геометрическая интерпретация задач.

На рис. 23 дана схема расположения автохозяйств (А_ь А₂, Аз, А4) относительно начального пункта А_о (базового автохо­зяйства) и указаны расстояния между всеми пунктами. Рас* смотрим 24 варианта (4!), состоящие из трех участков, груп-

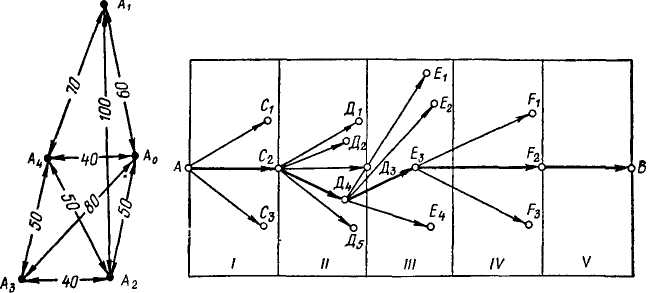
Рис. 23 Схема расположения автохозяйств. Рис. 24. Выбор оптимального маршрута.

пируя их по последнему пункту (табл. 12, первый шаг). Из табл. 12 выбрано только 12 наиболее экономичных по пробегу вариантов. При этом сравнивали два варианта, относящихся к одному и тому же множеству пунктов и оканчивающихся в одном и том же пункте. Вариант с меньшим суммарным про­бегом считается экономичным. Например, в вариантахA₀AiA₂A₄

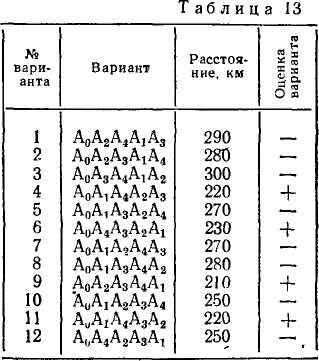
и AoA₂AiAi суммарные пути соответственно равны 210 км (60+100+50) и 220 км (50+100+70). Выбираем первый вари­ант (210 км). Далее проанализируем 12 наиболее перспектив* ных вариантов. Из 12 вариантов табл. 13 (второй шаг) выби->

раем четыре наиболее экономичных. В табл. 14 (третий шаг) из четырех вариантов, оканчивающихся в одном и том же пункте, берем два оптимальных маршрута движения ПДС А0А2А3А4А1А0 и AoAiAiA^Ao, имеющих минимальную длину (270 км).

Рассмотрим другой пример динамического программировав ния. Пусть требуется установить маршрут движения автомобиля из пункта А в пункт В (рис. 24). Надо выбрать вариант с наи­меньшей стоимостью (расстоянием, временем движения). На первом этапе вычисляем стоимость всех трех вариантов (ЛС_Ь АС₂ и АСг) и выбираем с учетом длины маршрута и возмож­ной скорости движения лучший вариант (например, АС₂). Да­лее точку С₂ соединяем со всеми точками D, — б_ъ и из пяти вариантов второго этапа выбираем лучший (например, C₂D₄). В дальнейшем — на третьем, четвертом и пятом этапах — посту*

паем так же. В результате получаем, что оптимальный марш­рут пройдет через пункты А — С₂ — D_A — Е₃ — Р^—В (жирная линия). При решении этой задачи должно быть проанализиро­вано 3+3-5+5-4+4-3+3-1 = 53 варианта.

5 6 1 8 9 10 11 12 13 П 15 16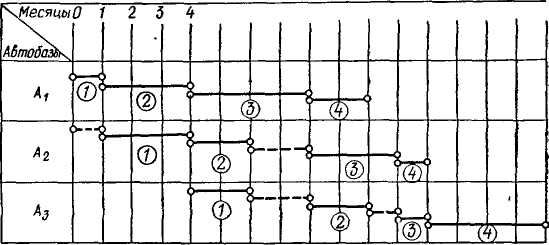

Рис. 25. График строительных работ.

Таблица 15

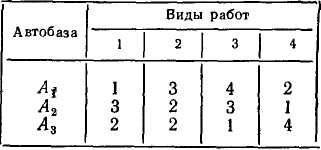
Рассмотрим более сложный пример по планированию строи­тельных работ [И]. Необходимо осуществить реконструкцию нескольких автопредприятий А\, А2,...,А_п. Ресурсы ремонтно-строительной организации ограничены, и выполнение одновре-менно одних и тех же работ на всех автопредприятиях невоз-можно. При реконструкции каждого автопредприятия необходи­мо выполнять в определенной последовательности различные работы (земляные, строитель­ные, монтажные, отделочные и др.). Принимаем, что один и тот же вид работ на разных объектах одновременно не мо­жет выполняться. Продолжи­тельность работ tij (i —1,2, ...,

п, /=1,2,..., т) для каждого автопредприятия в месяцах задана. Необходимо так спланировать сроки начала строитель­ных работ каждого автопредприятия, чтобы суммарный срок реконструкции был минимальным.

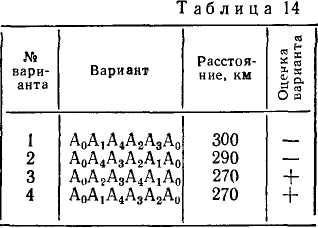
В табл. 15 для трех автобаз и четырех видов работ указаны необходимые сроки выполнения работ. Следует рассмотреть 6 вариантов (3!) реконструкции автобаз и лучший из них дол­жен быть выбран путем перебора всех вариантов (А1А2А3, Л1Л3Л2, А₂А_{А_г, А₂А₃А_и А_ъА_хА_г, Лз/Mi).

Рассмотрим график работ по автобазам А\, А₂ и Л₃ (рис.25). Автобаза А\ заканчивает все виды работ через 10 месяцев. Автобаза Л₂ может начать работу только через месяц после начала работы в автобазе Ai и затем вынуждена после выпол-

нения работ второго вида прервать работы на 2 месяца Общий простой составит 3 мес. Таким образом, чтобы в автобазе А₂ работы велись без перерыва, их необходимо начинать через 3 мес. после начала работ в автобазе Ль Анализируя таким образом начало работ на всех автобазах при различных вариант тах реконструкции, выберем наиболее приемлемый вариант, когда время реконструкции автобаз будет наименьшим.

Рассмотрим более подробно первый вариант. Для первой автобазы А\ сроки окончания работ равны: для первого вида работ— 1 мес, для второго 1+3 = 4 мес, для третьего 4+4 = = 8 мес. и четвертого 8+2= 10 мес. На второй автобазе опре* деленный вид работ может начинаться только после окончания этих работ на первой автобазе. Начало работы должно удовлет­ворять следующим неравенствам: первый вид t₂ > 1, второй вид — ^2+3 >• 4, третий вид — ^₂+5 >8, четвертый вид — ^2+8 >10. Из этих неравенств следует, что наименьшее значе­ние t₂, удовлетворяющее всем неравенствам, составляет 3 мес, и самый ранний возможный срок начала реконструкции второй автобазы — 3 мес. после начала реконструкции автобазы А\. Сроки окончания всех видов работ по автобазе Л₂ соответст-венно равны 3+3 = 6 мес, 6+2 = 8 мес, 8+3= 11 мес, 11 + 1 = 12 мес

Для третьей автобазы Л₃ система нера* венств запишется так: t₃ > 6, U + 2 >8, ^з + 4 > И, ^з + 5> 12. Минимальный срок U равен 7 мес, а сроки окончания остальных видов работ составляют 7 + 2 = 9 мес, 9 + 2=11 мес, 11 + 1 =12 мес и 12+4 = 16 мес. Общее время реконструкции всех трех автобаз—16 мес. Рассмотрим пятый вариант (табл. 16)

Окончание работ на автобазе Лз — 2, 4, 5, 9 мес. соответ­ственно. Начало работ на А\: t\>2, t\ + 1 > 4, U + 4 > 5, *i + 8 > 9 {t\>2, U>3, t\>\, ti>l, наименьшее значение ti=3). Окончание работ на А\\ 3 + 1 = 4, 3 + 4 = 7, 3 + 8 = = 11, 3+10=13 мес. Начало работ на Л₂: t₂> 4, t₂ + 3 > 7, ?₂ + 5>ll, *₂ + 8>13 мес. (t₂ > 4, t₂ > 4, t₂ > 6, t₂> 5, наи­меньшее значение t₂ = 6 мес). Окончание работ на Л₂:6 + 3 = = 9, 6 + 5=11, 6 + 8 = 14, 6 + 9= 15 мес.

Общее время реконструкции автобаз для всех шести вари­антов составляет 16, 16, 18, 17, 15, 16 мес. соответственно. Опти­мальный вариант •— пятый, время реконструкции всех автобаз здесь наименьшее— 15 мес.

Типичными задачами динамического программирования являются задачи по распределению в начале года имеющихся средств между предприятиями с целью получения максималь­ного суммарного дохода от их деятельности. Управление про-

цессом состоит в распределении и перераспределении средств. Шаг управления — выделение средств в начале года. Можно сразу искать оптимальное решение, но проще искать его посте­пенно шаг за шагом. Идея постепенной шаговой оптимизации положена в основу динамического программирования. Выбирая шаговое управление, необходимо учитывать его последствия в будущем. Только последний шаг можно, планировать «без учета будущего». Он должен приносить максимальный эффект. К нему затем постепенно пристраиваются предпоследние шаги [14].

Рассмотрим пример планирования работы двух автотранспорт­ных предприятий на пятилетний период. Допустим, выделено 2о тыс. руб. и эти средства надо наиболее эффективно распреде­лить на пятилетний срок между двумя АТП. Средства, выделен­ные первому и второму АТП, обозначим соответственно через х и у. Доходы за год первого и второго АТП можно предста­вить в виде функций дохода f(x) = 3- Ю~^ъх² и g(y) — 4-10~⁵у². Первоначально выделенные средства частично уменьшаются (тра­тятся) Остаток средств АТП после работы определяется «функ­циями траты» ср (х) — 0,6 х и ф (у) = 0,2 у.

В конце каждого года происходит перераспределение средств между АТП. Принимаем, что доходы накапливаются отдельно и в производство не идут, а неиспользованные средства (оста­ток) ср (х) и (Ь (у) вкладываются в производство в следующем году. Новые средства (сверх начального вклада) не поступают. Необходимо так распределить выделенные средства, чтобы общий доход двух АТП за пятилетку был наибольшим, т. е. W = W_max.

Управление u_t на i-шаге сводится к выделению средств xi и ус обоим АТП на этом шаге. Управление операцией складывается из всех шаговых управлений, т.е. и = (щ, «2, •••, «s)- Перед каждым шагом состояние системы характеризуется величиной 2,_i — количеством средств, оставшихся от предыдущих i — 1 шагов. Если для АТП-1 выделено xt средств, то для второго АТП y_t определится' как разность (zi—\—Xi). Доход на i-шаге будет равен

Рассмотрим распределение средств по годам.

1. Условное оптимальное распределение на последнем (пятом) шаге определяется по величине средств, выделяемых первому АТП и приносящих максимальный доход на пятом шаге:

где z₄ — остаток средств после четвертого шага; ш₅ — возмож­ный доход.

Знак 0 < Хь < 24 означает, что максимум берется по всем неотрицательным вложениям Хь (xt) и не превышает наличных средств 2₄(2i_i).

Второе АТП получит у₅ средств, причем у_ъ — (z₄—jfc). Воз­можный доход двух АТП в зависимости от управления хь составит

Определим максимальное значение дохода двух АТП на послед-

нем шаге, для чего продифференцируем приведенное выражение по хь-

Вторая производная —j = 14 • 10~⁵, т. е. дх₅

Рис. 26. Выбор мак­симального значения дохода.

больше нуля, поэтому парабола выпукла вниз и максимум функции достигается на границах отрезка 0—z₄ (рис. 26).

Подставив в выражение ш_Б(л:5, z₄) гра­ничные значения, определим точку макси­мума:

Итак, максимум достигается при х₅ = 0, когда все средства передаются на пятом шаге второму АТП (так как 4- 10~⁵zf> > 3 • 10—⁵2"f) • Это вполне естественно, поскольку функция дохода у второго АТП больше, а трата средств нас не лимитирует (процесс завершается). Наоборот, надо стремиться их полностью израсходовать.

Таким образом, последний шаг принесет доход <о₅ = 4 х X 10~⁵z₄, где z₄— остаток средств после четвертого шага (года).

2. Распределим средства на четвертый год. Пусть после треть­его года запас средств составит z₃. С учетом дохода на пятом шаге условный максимальный доход за два последних года оп­ределим по формуле

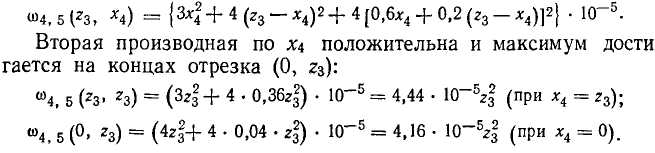
Итак, максимум ш₄,₅ (гз, х₄) достигается при х\ = z₃. Таким образом, на этом шаге все средства следует передать первому АТП.

3. Распределение средств на третий год. Условный макси­мальный доход за три последние года определим по формуле

большого числа предприятий (10—20) и на более длительные пе­риоды (10—15 лет), задача значительно усложняется, ее необхо­димо решать на ЭВМ.

Теория массового обслуживания. Под системами массового обслуживания подразумеваются сложные системы, предназна­ченные для обслуживания людей и машин (медицинское обслу­живание, телефонная и телеграфная связь, продажа билетов в

Год пятилетки	Распределе­ние средств между АТП		Итоги хозяйственного года
	1АТП	2АТП	остаток средств	доход
1 2 3 4 5	At 21 z2 г3 0	0 0 0 0 г*	0,600г0 0(360г0 0,216г0 0,129г0 0,02б20	3 ■ ИГ6** 1,08 • 10—Бг§ 0,389 • 10~5Zq 0,140 • 1О~5го 0,066 • Ю~5го

кассах, техническое об-Таблица 17 служивание автомоби­лей, снабжение зап­частями, заправка бен­зином на бензозапра­вочных станциях, гру­зовые и пассажирские перевозки и т. д).

В этих системах протекают случайные процессы, и эффектив­ность их работы зави­сит от ряда случайных факторов. Для того чтобы определить чис­ловые параметры, ха­рактеризующие эффек­тивность операции, и выбрать оптимальное решение, необходимо построить прежде всего математические (вероятностные) модели данных операций. Для описания слу­чайных процессов в некоторых физических системах применя­ется специальный математический аппарат теории вероятно­стей— теория массового обслуживания (ТМО). Эта теория является удобным инструментом для решения ряда актуальных транспортных задач.

Если случайный процесс протекает таким образом, что для каждого момента времени вероятность любого состояния систе­мы в будущем зависит только от состояния системы в настоя­щий момент и не зависит от того, каким образом развивался процесс в прошлом, такие случайные процессы называются марковскими или «процессами без последствия». В практике мно­гие случайные процессы можно считать марковскими, поэтому теория марковских процессов широко используется при постро­ении многих математических моделей операций и составляет основу теории массового обслуживания.

Случайные процессы могут быть с дискретным состоянием и непрерывным. В случайных процессах с дискретным состоя­нием система переходит из одного состояния в другое скачком (мгновенно). В системах с непрерывным состоянием процесс протекает сравнительно плавно (например, изменение скорости

движения автомобилей на дороге). Ниже рассмотрены только случайные процессы с дискретным состоянием.

Каждая система массового обслуживания (СМО) включает в себя входящий поток требований, множество обслуживающих единиц (приборов, каналов, линий) и определенный порядок (дисциплину) обслуживания. Системы могут быть одноканаль-ные и многоканальные.

В случайные моменты времени в систему поступает поток требований (заявок). Заявка обслуживается в течение какого-то времени, после этого «канал» освобождается и система может начать обслуживание следующей заявки. Пропускная способ­ность системы зависит от числа каналов и их производитель­ности.

С помощью теории массового обслуживания можно устано­вить зависимости между характером потока заявок, произво­дительностью одного канала, числом каналов и эффективно­стью обслуживания, которая может характеризоваться средним временем ожидания в очереди, вероятностью немедленного об­служивания заявки, средним временем простоя отдельных кана­лов, средним доходом в единицу времени и т. д.

Для математического описания любой системы массового обслуживания необходимо знать поток заявок, который следует рассматривать как поток случайных событий. '

Простейший поток событий обладает тремя основными свой­ствами: стационарностью, отсутствием последействия и орди­нарностью.

Стационарным (или простейшим пуассоновским) называется такой поток, в котором вероятность появления определенного числа заявок в течение некоторого промежутка времени не зави­сит от начальной точки этого промежутка, а определяется лишь его длиной. Для стационарных потоков характерна постоянная плотность потока (среднее число заявок в единицу времени X=const). Если поток нестационарный, интенсивность потока требований зависит от времени (X=f(t)). Для нестационарных потоков аналитические решения практически отсутствуют.

Термин «отсутствие последействия» употребляется в том случае, если вероятность поступления требований после произ­вольного момента времени не зависит от характера поступления требований до этого момента. Другими словами, заявки посту­пают в систему независимо друг от друга.

Если невозможно одновременное появление двух и более требований или вероятность их появления пренебрежимо мала по сравнению с вероятностью появления одного события, такой поток называется ординарным. Если поток неординарный и за­явки поступают только парами или тройками (пакетами), то его можно свести к ординарному, рассматривая поток как поток «пар» или «троек». В качестве примеров неординарных потоков событий со случайным числом событий в пакете могут быть

спаренные автобусы, автопоезда с одним или двумя прицепами или с несколькими контейнерами и т. д.

В практике наблюдаются отклонения от простейших потоков. Например, в течение суток поток автомобилей на данной дороге меняется в значительных пределах. Поток автомобилей можно считать стационарным только в определенные часы суток (ут­ром, в середине дня, вечером). Появление какого-либо важного письменного распоряжения или телефонного звонка вызывает целый поток других распоряжений или звонков. Это пример появления последействия.

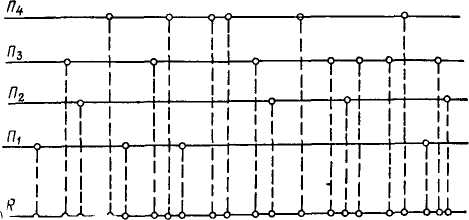
Рис. 27. Пример образования пуассоновского потока.

Если в билетную кассу обращаются с просьбой продать не один, а сразу несколько билетов, нарушается ординарность.

Простейшие потоки (с постоянными интенсивностями) явля­ются наиболее общими, поэтому они играют особую роль в тео­рии массового обслуживания. Если поток заявок отличается от простейшего, в ряде случаев его можно заменить простейшими потоками с той же плотностью.

При суммировании (суперпозиции, взаимном наложении) не­скольких (достаточно 4—5) ординарных потоков, примерно рав­номерных и малых по сравнению с суммарным, практически с любым последействием получается поток, очень близкий к про­стейшему. Последействие в суммарном потоке, даже если оно сильно выражено в отдельных потоках, постепенно слабеет. На­пример, если автомобили из разных пунктов погрузки П_ь П₂, Пз, П₄ (рис. 27) независимо друг от друга поступают по разным марш­рутам в конечный пункт разгрузки R, то образуется пуассонов-ский поток с определенными параметрами отличными от пара­метров слагаемых потоков. В каждый промежуток времени (отрезок) т автомобиль может случайно поступить из любого пункта погрузки.

Стационарные ординарные потоки с ограниченным последей­ствием являются более общими по сравнению с простейшими и называются потоками Пальма.

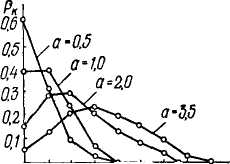
Часто случайные величины распределяются по закону, кото­рый называется законом Пуассона. Допустим, имеется прерыв­ная случайная величина х, принимающая целые неотрицатель-

ные значения О, 1, 2, ...k. Если эта величина х распределена по закону Пуассона, то вероятность того, что она будет иметь зна­чение k, выражается формулой

2,

k -

где а—параметр закона Пуассона.

Кривые распределения случайной величины х показаны на рис. 28. Сумма всех вероятностей Р_к в каждом многоугольнике равна единице, что нетрудно доказать.

Запишем

2 ^Pk = J2 a^klk\e-^a = е-* 2 a^klk\

fc=0 *=0 fe=0

Поскольку

^{= е}°> окончательно имеем

Параметр а является математическим ожиданием случайной величины х. Дис­персия случайной величины равна ее ма­тематическому ожиданию а. По этому свойству распределения можно проверять

гипотезу о том, что случайная величина / 2 3 О" 6 "7 к

распределена по закону Пуассона, для _{Рис 28} р_аспр_еделение чего из опытов определяют статистиче- случайной величины. ские характеристики.

Для пуассоновского потока величина а равна интенсивности потока, умноженной на длину интервала, т. е. а = Xt.

Для стационарных ординарных потоков без последствия веро­ятность P_k (t) появления k требований в промежутке времени длиной / подчиняется распределению Пуассона с параметром Xt:

где \— интенсивность потока (среднее число требований за единицу времени, X = 1//_тр).

Вероятность того, что ни одна заявка (k = 0) не поступит в течение времени t, определится по формуле

М) V) —

(It)⁰

01

С увеличением t вероятность того, что не поступит ни одна заявка, быстро уменьшается, причем скорость снижения будет тем выше, чем больше X.

Рассмотрим интервал Т заявок между соседними событиями простейшего потока. На оси ot (рис. 29) найдем закон распре­деления данной случайной величины Т. Функция распределения

83

величины 7' будет F (t) = 1—е~^и. Плотность распределения f (t) случайной величины Т получим, если продифференцируем выра­жение F (t) по /: / (t) = dFldt = ке~^и.

Этим законом можно описать многие случайные процессы, например прибытие автомобилей в пункт погрузки (рис. 30). Длительность промежутков времени между последующими по­ступлениями автомобилей разная (м, ь, . . .). Она хорошо описы­вается экспоненциальным распределением F (t) = \— Р (t) = 1 — — e~^xt, где X—параметр, характеризующий интенсивность дви­жения. Он равен М_ср, где t_cp — средний интервал прибытия автомобилей.

t_s U t₇ t_s

Рис. 29. Вероятность попадания величины Т в заданный интервал. Рис. 30. Интервалы между прибытиями автомобилей.

Закон распределения с плотностью f(t) называется показа­тельным (экспоненциальным). Параметром закона является вели­чина \. Нетрудно доказать, что математическое ожидание (среднее значение) m и среднее квадратичное отклонение о при таком законе обратны X, т. е. m = а= 1 Гк = t_cp.

При построении моделей систем массового обслуживания, кроме характеристик входного потока требований, необходимо знать число каналов и время обслуживания одного требования Тоб, которое может быть как случайной величиной, так и неслу­чайной.

Случайная величина Т_оа чаще всего имеет распределение по экспоненциальному закону и плотность распределения g(t) — = 1>.е~^, где параметр jj.— величина' обратная среднему времени эбслуживания одного требования (Мер. об). Время обслуживания может также описываться и другими законами (Эрланга, Вей-булла, нормальным). Например, для скорой медицинской служ­бы, технической помощи, аварийных служб входящий поток описывается нестационарным пуассоновским, а длительность об­служивания подчиняется распределению Вейбулла. Однако вслед­ствие того, что пропускная способность и другие характеристики систем массового обслуживания зависят в основном от среднего значения времени обслуживания 4_Р.об, а не от закона распреде­ления времени обслуживания, применяется в основном показа­тельный закон. Это упрощает математический аппарат и позво­ляет получить сравнительно простые аналитические формулы.

Рассмотрим несколько наиболее общих моделей систем мас­сового обслуживания [14].

Модель 1. Система массового обслуживания с отказами. В си­стемах с отказами, когда все каналы заняты, поступившая заяв-

ка получает отказ и в дальнейшем в обслуживании не участву­ет (например, отсутствие билетов в кассе, нет мест).

Допустим, на вход системы поступает простейший поток заявок с плотностью X. Время обслуживания Т_оь изменяется по показательному закону с параметром р. = 1/4р.об- Система рабо­тает в установившемся (стационарном) режиме. В начале работ системы может наблюдаться нестационарный («переходной») про­цесс (процесс запуска системы).

Примером простейшей задачи теории массового обслуживания является задача о функционировании одноканальной системы с отказами. Система х, представленная графом состояний на

Рис. 31. Система с одним каналом. Рис. 32. Система с п каналами.

рис. 31, может находиться в одном из двух состояний: хо— канал свободен, х\ — канал занят. Из состояния хо в состояние х\ переводится поток заявок с интенсивностью X, а из ^ в хо — поток обслуживании с интенсивностью р.

Система хо с п каналами (рис. 32) может иметь множество состояний:

хо — свободны все каналы; Х\ — занят один канал; Хг — занято два канала;

Xk — занято k каналов;

х_п — заняты все п каналов.

Прямые стрелки на рис. 32 показывают возможные переходы системы из одного состояния в другое. Закругленные означают, что системы могут оставаться и в прежнем состоянии. При на­личии одного канала поток обслуживания имеет интенсивность р, при k каналах поток обслуживания в k раз интенсивнее {k\y).

Обозначим отношение среднего числа заявок, приходящих в СМО за среднее время обслуживания одной заявки Х/р. через а, и назовем его приведенной плотностью потока заявок или при­веденной интенсивностью. При ja = 1//_ср.об <* = Х4_Р.об.

Вероятности состояний системы в установившемся режиме

Ро, Р\, ..., Pk, ■.., Р_п в общем виде определяются по формуле

k Pk=-rrPo. Поскольку

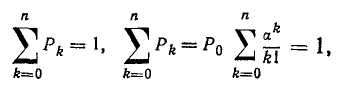
вероятность того, что система вообще не загружена (все каналы свободны), такова:

Для простейших потоков и практически при любом законе распределения времени обслуживания справедлива формула Эрланга, дающая предельный закон распределения числа заня­тых каналов с учетом характеристики потока заявок и произво­дительности системы:

Эта формула может быть применена и для потоков с не очень большим последействием и допускает ожидание заявки в очереди, если срок ожидания мал по сравнению со средним вре­менем обслуживания одной заявки. При k = п вероятность того, что поступившая заявка найдет все каналы занятыми (вероят­ность отказа), определится по формуле

Другими словами, вероятность отказа />_отк является средней долей не обслуженных заявок среди поданных (поступивших).

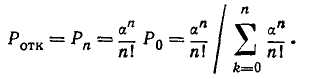
Для систем массового обслуживания с отказами важными характеристиками эффективности системы являются абсолютная пропускная способность (среднее число заявок, которое может обслужить система за единицу времени) и относительная про­пускная способность (средняя доля поступивших заявок, обслу­живаемых системой).

Зная относительную способность q = (I—Ротк), можно опре­делить абсолютную пропускную способность: A =\q.

Для одноканальной системы (при п = 1) Р_Отк = Pi = а/(1 + <*). Относительная пропускная способность q = 1 — а/(1 + а) =

= 1/(1 + а). Другими словами, поскольку а= —, то q =

Пример. Станция технического обслуживания автомобилей имеет 4 поста. На станцию поступает простейший поток заявок с плотностью X = 6 (заявок в час). Средняя длительность технического обслуживания t_{cp об} = 1 ч. Если все посты заняты, прибывший автомобиль получает отказ. Необходимо опре­делить вероятность отказа, относительную и абсолютную пропускную способ­ность системы и среднее время, в течение которого посты на станции не загружены.

(около 47% поступивших автомобилей получат отказ).

3. Установим относительную пропускную способность системы q — 1 <— — ^отк ⁼ 1 — 0>47 = 0.53 (в установившемся режиме система будет обслужи­вать около 53% поступивших заявок).

4. Абсолютная пропускная способность А = \q = 6-0,53 = 3,18 (станция способна осуществлять в среднем 3,18 обслуживании в час). 5. Вероятность того, что система не загружена

(вероятность мала и составляет около 0,87%).

Если эту задачу решать как детерминированную и принимать, что на станцию технического обслуживания прибывает ровно 6 автомобилей в час и ровно через час заканчивается обслуживание автомобиля, то в течение одного часа будет обслуживаться ровно 4 автомобиля.

Вероятность обслуживания за 1 час прибывших автомобилей равна 4 ■g- = 0,665. Абсолютная пропускная способность станции — 4 автомобиля в час.

Сравнивая эти результаты с полученными выше, можно сделать вывод, что при вероятностном подходе результаты примерно на 20% ниже, чем при детерминированном подходе (относительная пропускная способность 0,665 и 0,53; абсолютная пропускная способность 4 и 3,18).

Модель 2. Система массового обслуживания с ожиданием. В системах с ожиданием поступившая заявка, когда все кана­лы заняты, становится в очередь и ожидает, пока не освободится какой-нибудь канал.

Система называется «чистой системой ожидания», если время ожидания в очереди ничем не ограничивается. Если есть какие-либо ограничения (например, время ожидания заявки в очереди, время нахождения заявки в системе или число заявок в очереди), система называется «системой смешанного типа».

Допустим, что на вход системы, состоящей из п каналов, поступает простейший поток заявок с плотностью )., время об-

Эта величина характеризует плотность «потока уходов» заявки, стоящей в очереди. Если за это время заявка не принята к обслуживанию, она покидает очередь.

При v ->- оо (t_cp_ _ож = 0) система смешанного типа становится «чистой» системой с отказами, а при v -> 0 (t_{cp О}ж = °о) — «чистой» системой с ожиданием.

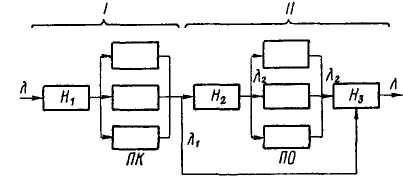
Системы массового обслуживания могут быть однофазные и многофазные. Примером двухфазной системы массового обслу­живания с ожиданием может служить станция контроля и тех­нического обслуживания автомобилей, структурная схема которой представ­лена на рис. 33. Поток автомобилей с интенсив­ностью X поступает на станцию контроля, со­стоящую из трех постов контроля (ПК)- Если все

Рис. 33. Структурная модель контроля (I) ™^{СТЫ занять1}' ^{т0 авт0М}°-

и технического обслуживания автомоби- ^оили поступают В зону

лей (П) ожидания (накопитель

Hi). После контроля ис­правные автомобили с интенсивностью ^ направляются в эксплуатацию через накопитель Нз. Неисправные автомобили с интенсивностью Яг через накопитель Нг поступают на посты тех­нического обслуживания (ПО). После устранения выявленных не­исправностей автомобили через накопитель Нз идут в эксплуа­тацию. Интенсивность потока из накопителя Нз равна интенсив­ности потока на входе первой фазы.

Для системы с п каналами возможны такие состояния: х₀ — все каналы свободны (очереди нет); x_i — занят один канал (очереди нет);

x _k — занято kканалов (очереди нет); х_п — заняты все каналы (очереди нет); х_п , [ •—заняты все каналы (одна заявка стоит в очереди);

х _п,_т—заняты все каналы (т заявок в очереди); х_п , _s — заняты все п каналов (s заявок в очереди).

Вероятности состояния системы для любого &< я определя­ются по формулам

Сомножитель Р_о, характеризующий вероятность того, что система вообще не загружена (все каналы свободны), определя­ется из выражения

Если вместо плотностей X и v ввести «приведенные» плотности Х/[а = Х/_Ср._Об = а и у/р, = v£_Ср.об = Р, в окончательном виде получим следующие выражения для вероятностей, состояний системы:

Чтобы определить вероятность того, что заявка покинет си­стему необслуженной (Р_н), т. е. найти отношение среднего числа заявок, уходящих из очереди в единицу времени, к среднему числу заявок, поступающих в единицу времени, необходимо ма­тематическое ожидание т_% числа заявок, находящихся в очереди,

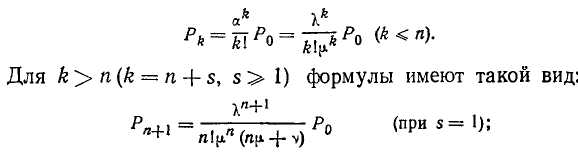
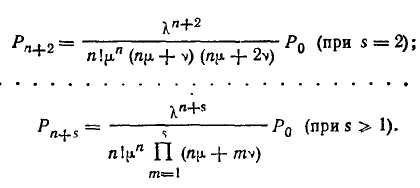
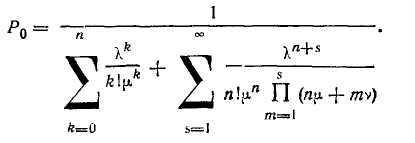
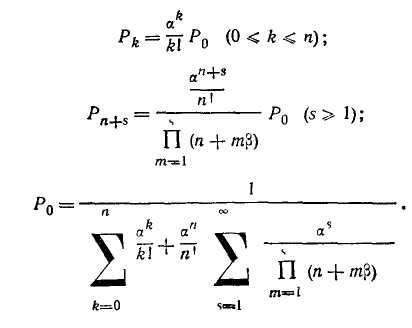
я

умножить на коэффициент —, показывающий отношение средней плотности уходов одной заявки v к средней плотности заявок

_I

Среднее число заявок, находящихся в очереди (средняя дли­на очереди),

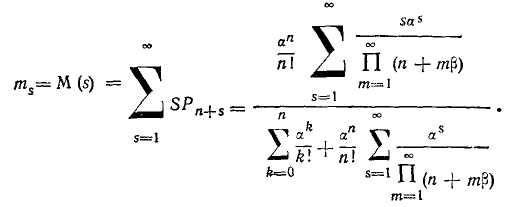
Вероятность того, что заявка не будет обслужена (Р_я), опре­делится по формуле

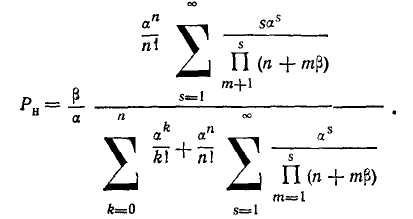
Относительная пропускная способность системы (вероятность того, что заявка будет обслужена) q = 1 — Р_и.

Если (3 -> со (/_ер.об == со), система с ожиданием превращается в систему с отказами (заявки немедленно уходят из очереди). При этом формула для P_n+S равна нулю.

Если (3 -> 0 (при 4р.об = 0), система становится «чистой» си­стемой с ожиданием (заявка не уходит из очереди и Р_а = 0).

В чистой системе с ожиданием ((3 -> 0) заявка не уходит из очереди, она все равно дождется обслуживания. Это может быть при а < п, т. е. когда среднее число заявок, приходящееся на время обслуживания одной заявки, не выходит за пределы п-канальной системы. При а > п число заявок, находящихся в очереди, все время будет возрастать.

Если, р -> 0, приведенные выше формулы (с. 89) запишутся следующим образом:

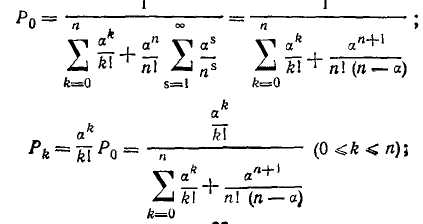
Среднее число заявок в очереди (средняя длина очереди) при О

,«+! ™^!('-^²

/ * \²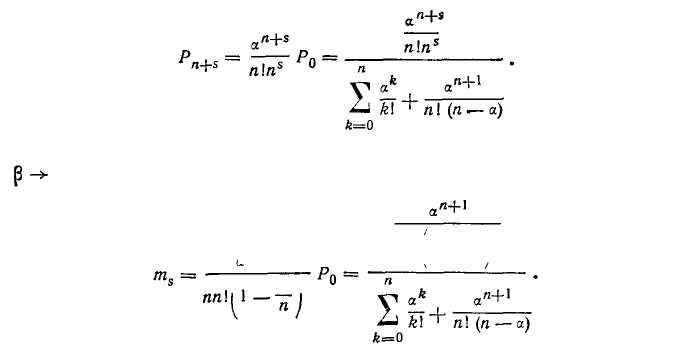

Пример. На трехпоетовую станцию технического обслуживания автомо­билей с неограниченным временем ожидания поступает простейший поток автомобилей с X = 4 автомобиля в час. Средняя продолжительность техни­ческого обслуживания одного автомобиля t _об = 0,5 ч. Необходимо опре­делить вероятности состояния Р_о, Р_х, Р₂, Рз, вероятность наличия очереди Р_оч и среднюю длину очереди tn_s.

Ре ш е н и е.

1. Определим параметр ft — величину, обратную среднему времени обслу­живания одного автомобиля,

Модель 3. Система смешанного типа с ограничением по длине очереди. Рассмотрим систему с ограничением по числу заявок, находящихся в очереди. Заявка становится в очередь только тогда, когда в нем находится менее т заявок.

Выражения для определения различных состояний системы в окончательном виде имеют следующий вид:

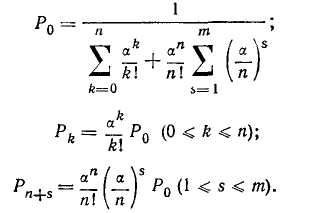
Вероятность того, что заявка покинет систему необслуженно й, определится выражением Р_п+т при т. заявок в очереди.

Пример. На станцию диагностики автомобилей поступает простейший по­ток заявок с плотностью X = 0,5 автомобиля в час. Имеется один пост диа­гностики. В помещении станции может находиться, ожидая очереди, не более трех автомобилей (/п = 3).

Среднее время простоя одного автомобиля t_{cp об} = — = 2 ч.

Необходимо определить пропускную способность станции диагностики и среднее время простоя станции, а также установить, как изменяются эти ха­рактеристики при наличии второго поста диагностики.

Относительная пропускная способность системы при я = 2 равна q= 1 —. — 0,021 = 0,979, а абсолютная Q == 0,5 • 0,979 = 0,49 автомобиля в час. Среднее время простоя двух постов диагностики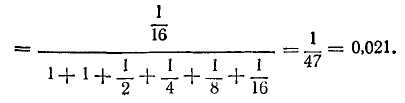

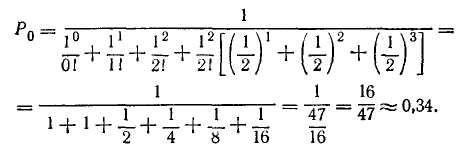
Во многих учебниках, как правило, описывается функциони­рование детерминированных систем и рассматривается регуляр­ный поток прибытия автомобилей на пункты погрузки — разгруз­ки, на станции технического обслуживания и т. д. по строгому графику (расписанию). Данное допущение с точки зрения науки не представляет интереса. Такие случаи в практике встречаются довольно редко. Автомобильный транспорт—одна из больших систем массового обслуживания, для которой характерны значи­тельные колебания времени, например, при прибытии грузовых автомобилей в пункты погрузки и разгрузки, на станции техни­ческого обслуживания и ремонта, на бензозаправочные станции и т. д. При этом возникают экономические потери и их необхо­димо уметь сокращать до минимума. Овладев в достаточной мере аппаратом ТМО, можно научиться управлять процессами массо­вого обслуживания путем влияния на входящий поток, на ско­рость обслуживания, на регулирование внутри очереди и т. д.

Сетевое планирование и управление. При исследовании опе­раций часто приходится решать сложные задачи планирования комплекса работ. Для решения таких задач применяются мате­матические методы сетевого планирования и управления (СПУ). Системы сетевого планирования и управления находят широкое применение в различных отраслях народного хозяйства (в стро­ительстве, машиностроении, транспорте, научно-исследовательской работе и т. д.). В нашей стране такие системы называются АСОР (автоматизированные системы организации работ) и СПУ (сетевое планирование и управление). В США, например, широко рас­пространена система под названием PERT (Program Evaluation and Review Technique — метод оценки и пересмотра планов).

Данные методы базируются на системном подходе к боль­шой управляемой системе с учетом многочисленных внутренних и внешних связей. Например, подготовка к производству нового автомобиля осуществляется не одним заводом и даже не одной отраслью. В создании и подготовке к производству автомобиля

принимают участие разные организации и заводы, конструктор­ские бюро и научно-исследовательские институты. Одни проек­тируют и подготавливают техническую документацию на двига­тель, другие — на ходовую часть, третьи — на электрооборудо­вание и т. д. Параллельно ведется разработка новых сортов автоэксплуатационных материалов, гаражного оборудования. Создается ремонтная база и предприятия для производства запасных частей.

Применение для крупных систем обычных методов планиро­вания по каждой'организации с помощью традиционных ленточ­ных графиков малоэффективно. Основным их недостатком явля­ется невозможность показать взаимосвязь отдельных работ, оце­нить значимость каждой работы в отдельности. Нельзя отразить динамичность разработок в связи с изменением сроков выпол­нения каких-либо работ. Динамичность присуща только сетевым методам планирования. При сетевом планировании и управлении исходные планы проектов представляются в виде сетевого гра­фика (сетевой модели, сети), что обеспечивает наглядность по­рядка выполнения отдельных операций во времени. Сетевой гра­фик— графическое воспроизведение сетевой модели реализации проекта, позволяющей проводить эксперименты, анализировать отдельные варианты и находить оптимальные решения при управлении процессом реализации (осуществления) того или иного проекта.

Практическое применение СПУ в конечном итоге способству­ет улучшению основных экономических показателей: сокращение сроков строительства (изготовления) и времени простоя — до 20—30%. В сложных СПУ можно широко использовать элект­ронно-вычислительную технику.

Опыт применения методов СПУ в нашей стране (на строи­тельстве, например, Бурштынской ГРЭС, Лисичанского химком­бината, блюминга-автомата в Челябинске) показывает, что наи­больший эффект от применения СПУ достигается на крупных стройках, на заводах серийного и массового производства, при выполнении комплексных научных исследований.

Методы СПУ успешно используются и для небольших систем, включающих в себя два — три десятка операций и событий. Дру­гими словами, этот метод пригоден для планирования больших и малых по объему комплексов работ. Практика расчета сетевых графиков показывает, что сетевые модели, имеющие до 200 ра­бот, могут успешно решаться вручную. Методы сетевого плани­рования помогают руководителю в выборе правильного ре­шения.

В сложных динамических системах в качестве основного по­казателя обычно выбирается минимальное время выполнения всего комплекса работ. Основу сетевого моделирования состав­ляют сетевые графики (граф-схемы), состоящие из заданных точек (вершин), соединенных определенной системой линий. Ли-

нии, соединяющие вершины, называются ребрами или дугами графа. В основу построения и анализа сетевых графиков поло­жена «теория графов». Работа на графах изображается ребрами (ориентированной стрелкой), а события — вершинами (круж­ками).

Все работы — операции на сетевой модели распределяются в технологической последовательности. Каждая работа начинает­ся и заканчивается событиями. Под собы­тием подразумевается окончание того или иного этапа работы (уборка автомобиля закончена, технический проект принят и т. д.). Каждой стрелке соответствует опре­деленная работа, принимаемая как про­цесс, а не результат (например, процесс мойки автомобиля). Работа зашифровывается двумя числами, соответствующими начальному и конечному событиям, а под стрелкой указывается продолжительность работы в месяцах, днях, часах, минутах. Длина стрелки не пропорциональна про* должительности операций. Например, событие / (рис. 34) ха« рактеризует начало работы /—2. Событие 2 характеризует окончание этой же работы и начало работы 2—3. Одно событие может быть началом нескольких работ. Точно так же одно событие может быть и окончанием многих работ.

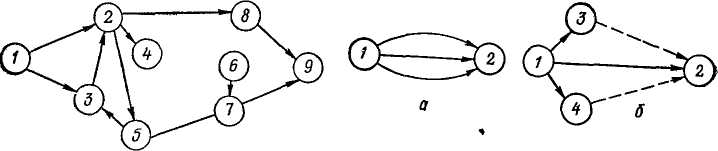
Рис. 35. К правилу построения сетевых графиков.

Рис. 36. К правилу построения сетевых графиков: а—неправильно; б—пра­вильно.

Важно уметь правильно построить сетевые графики. При со­ставлении сетевых графиков необходимо придерживаться опре­деленных правил. Рассмотрим основные из них.

1. В сетевых графиках не должно быть событий, которыми не начинаются работы (кроме завершающего события) или ко­торым не заканчивается ни одна работа, если оно не является начальным. Например, события 4 и 6 на рис. 35 являются тупи­ковыми. Событие 4 или не нужно для выполнения всего комплек­са работ, или для него ошибочно не указана связь. Наличие события 6 свидетельствует или об ошибке при вычерчивании се­ти, или о том, что не запланирована какая-то работа, без кото­рой не может произойти это событие.

2. Сетевой график не должен иметь замкнутых контуров (как 2—5—3 на рис. 35), в которых какое-то событие соединяется с ним самим. Такая ситуация невозможна.

3. При изображении параллельных работ в сети не должно быть событий и работ с одинаковыми номерами. Чтобы этого избежать, надо ввести дополнительные события и фиктивные (рис. 36) работы.

Рис. 37. К правилу построения сетевых графиков, а — неправильно;

б — правильно.

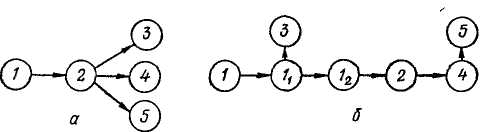
4. Если, например, работы 2—3 и 2—5 (рис. 37) могут быть начаты при частичном выполнении предыдущей работы )—2, то на сети вводятся промежуточные события li и Ь.

5. Если в событие, например 4 (рис. 38), входит и выходит по несколько работ и для выполнения некоторых работ, выхо­ дящих из данного события, необходимо получить результаты не всех работ, входящих в событие, а только части из них, то нуж­ но ввести фиктивную работу и дополнитель­ ное событие.

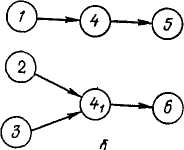
правилу построения сетевых а — неправильно; б — пра­вильно.

Рис 38. К графиков:

Существует также определенный порядок нумерации событий графика. Обычно вер­шины нумеруют по правилу вычеркивания дуг. Суть этого прави­ла состоит в следую­щем. Каждому собы­тию графа присваивается соответствующий ранг. Начальному событию присваивается нулевой ранг. Далее мысленно вычер­кивают событие нулевого ранга и все исходящие из него дуги. В этом случае ряд событий будет иметь только исходящие дуги. Таким событиям присваивается первый ранг, и они нумеруются в произвольном порядке от 1 до п. Затем вычеркиваются собы­тия первого ранга и все исходящие из них дуги. События, имеющие только исходящие дуги, называются событиями вто­рого ранга. Их нумеруют в произвольном порядке от п -К 1 до «1. Аналогично определяются события более высоких рангов. Пронумеруем вершины графа, представленного на рис. 39. Событию А присваивается нулевой ранг. Если вычеркнуть все

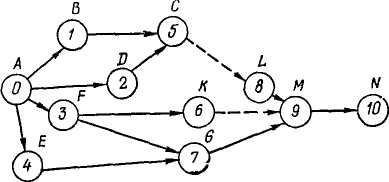
Рис. 39. К примеру нумерации- вершин графя.

дуги, выходящие из события А, то события В, D, F, Е будут иметь только исходящие дуги. Им присваивается первый ранг в про­извольном порядке, и они нумеруются от 1 до 4. Затем вычер­киваем дуги, выходящие из событий первого ранга, и находим события только с ис­ходными дугами (С, К, G). Им присваивается второй ранг, и они ну­меруются в произволь­ном порядке от 5 до 7. Снова вычеркиваем дуги, выходящие из со­бытий второго ранга, и находим события только с исходящими дугами. Таким собы­тием будет событие L. Это событие уже третьего ранга. Прону-меруем его цифрой 8. Таким же образом можно определить со­бытия четвертого М и пятого N порядков. Обозначим их циф­рами 9 и 10.

Важное значение в сетевом планировании и управлении име­ет понятие «путь» —■ любая последовательность работ от начала графа к его концу. Отдельные пути будут иметь различную про­должительность. Путь, имеющий наибольшую продолжитель­ность, называется критическим. Критический путь определяет

наименьшие затраты времени для выполнения всего комп­лекса работ. Работы, распо­ложенные на этом пути, назы­ваются критическими, и им должно уделяться максималь­ное внимание.

Рис. 40. Пример сетевого графика.

Продолжительность рабо­ты оценивается тремя показа-телями. Обычно определяется максимальная продолжительность (пессимистическая опенка), минимальная продолжительность (оптимистическая оценка) и наиболее вероятная продолжительность.

Рассмотрим краткую методику расчета параметров сетевых моделей на примере сетевого графика, представлелного на рис. 40.

Введем следующие обозначения:

i— номер начального события чля рассматриваемой работы) / — номер конечного события для этой работы; /. — полный путь; L(i, /)—путь от начального события сети о номером i к какому-либо

событию с номером /;

L(i, с) —путь от какого-то события i к конечному событию сети с но­мером с;

L(i_nt t_m) — путь между какими-либо (не начальными и конечными) собы­тиями t_n и i_m\

t(L_t) — продолжительность пути;

t(i)— продолжительность свершения какого-нибудь события «; /(^ — продолжительность сверления конечного события с; 'min ('• /) — минимальн ш продолжительность работы (f, j) (оптимистиче­ская оценка);

/_шах ((,/)-— максимальная продолжительность (пессимистическая оценка); t_HB(i, /) —наиболее вероятная продолжительность; R (L) — резерв времени пути; R (t) — резерв времени события; R_n ('• /')—полный резерв времени.

Продолжительность пути складывается из продолжительно-стей отдельных работ, входящих в этот путь. Например, продол­жительность пути 1—4—7 равна 3 + 6 = 9.

На приведенном сетевом графике всего шесть полных путей с различной продолжительностью:

1,(1,2,5,7) -W(L,) = 5 + 4+1 = 10

L_a(l, 4, 5, 7) -W(Z.₂) = 3+1+1=5

L₃(L 4,7) -**(L₃) = 3 + 6 = 9

L₄ (1, 3, 4, 5, 7) -+ t (L₄) = 10 + 0 + 1 + 1 = 12

L₅(l,3, 4, 7) -W(Z,₅)= 10 + 0 + 6= 16

L₆(l, 3,6,7) -»/(L₆) = 10+2+2= 14

Критическим является путь Ls, имеющий наибольшую про­должительность (16 единиц). Для сокращения этого срока надо сокращать продолжительность работ, лежащих на этом пути (работа 1—3 или 4—7).

При анализе сетей определяются ранние и поздние сверше­ния событий, ранние и поздние сроки начала и окончания работ, резерв времени пути и резерв времени событий. При более де­тальном анализе устанавливаются и другие параметры: частные резервы времени, свободные резервы времени, коэффициенты напряженности работ, коэффициенты резервов времени работ.

Определим ранние и поздние сроки свершения событий. Обо­значим -поздний срок свершения события i через t_n (i), ранний — через t_p(i). Наиболее ранним ероком свершения конечного со­бытия является продолжительность критического пути. Для дру­гих событий f_p(i) равен суммарной продолжительности работ, лежащих на максимальном из путей, ведущих к данному собы­тию сети от начального, т. е. t_p(i) ~t[L(i, /)_mtx]. Например, для события 5

/_р (5) = / [I (1, 5)]_тах = / (1, 3. 4, 5) = ю + о + 1 = П.

При сетевом планировании ставится цель выполнения всего комплекса работ в кратчайший срок, поэтому для конечного со­бытия наиболее поздний орок его евершения равен наиболее

раннему, т. е. ?_р (с) = t_n (с). Для остальных событий поздний срок свершения события t_n (0 равен разности между продолжитель­ностью критического пути и суммарной продолжительностью работ, которые лежат на максимальном из путей, идущих от данного со­бытия к конечному событию о, т. е. t_n\i) = t_Kf— t[L(i, c)_max].

Так, для события 3/„(3) = 16— t[L(3, 7)_max] = 16 — /(3, 4, 7) == 16 — 0— 6= 10. Таким образом, при заданном сроке свер­шения конечного события сети (16 единиц) событие 3 не может совершиться позже, чем через 10 дней после свершения началь­ного события.

Определим ранние и поздние сроки начала и окончания ра­бот. Если известны ранние и поздние сроки свершения событий, то для каждой работы можно определить t_pB (i) — самый ранний из возможных сроков начала работы (/, /), /_Пн(г, /) — самый позд­ний срок начала работы (i, j), t_po{i, j)— самый ранний срок окон­чания работы (t, /), tao(i, j)— самый поздний срок окончания работы (i, /).

Расчет обоих сроков может быть осуществлен с помощью сле­дующих формул:

<_ри С /) = 'р (0; <п„ V, D = <_п (/') - < С О: ⁽_Ро С I) = '_Р (0 + t(t.m 'по С D = 'п (/')•

Для работ критического пути /_рв (t, f)—t_m(i, /); t_po(i, j) = = t_no(i, j). В качестве примера определим все показатели для работы 4-5: /_рн (4, 5) = t_p (4) = 10; t_m(i, 5) = /_п(5)- t(4,5) = = 15- 1 = 14; /_ро(4, 5) = t_p (4) + /(4,5) = 10 + 1 = 11; /_по(4, 5) = *= U (5) = 15.

Резерв времени пути R (L) определяется как разница между продолжительностью критического t_Kp и какого-нибудь другого пути t(L): R(L)=t_Kp — t(L). Этот резерв показывает, насколько можно увеличить в сумме продолжительности работ, принадле­жащих пути L, чтобы при этом общий срок выполнения всего комплекса работ не изменился. Так, резерв времени для пути (1,2,5, 7) составит /_кр — /(1, 2, 5, 7) = 16 — (5 + 4 + 1) = 6. Следовательно, продолжительность отдельных работ (1, 2), (2, 5) и (5, 7) в сумме можно увеличить на 6 единиц. При этом общий срок выполнения комплекса работ не изменится и останется равным 16.

Резерв времени события — как разница между поздним и ран­ним сроком свершения событий: R (i) == t_n (i) — t_p (i). События, принадлежащие критическому пути, резерва времени не имеют. Для события 5 резерв времени равен

Я(5)=/_п(5)~/_р(5)=15-11=4,

Резерв времени для события i показывает, на какое время можно задержать свершение этого события, чтобы общий срок выполнения комплекса работ не увеличился.

Полный резерв времени работы определяется по формуле Я_п(⁽. /) = <„(/)-<_р ©-<(«. О-

Пользуясь формулой, установим резерв времени для работы (4, 5). Поскольку *„(5) =*к_Р — t[L(5, 7)_mdX] = 16— t(5, 7) = 16 — — 1 = 15; *_P(4) = /[L(1, 4)_maxl ="/(1, 3, 4) = 10 + 0= 10 at(i, j) = 1, величина R_n {i, /) = 15— 10— 1 = 4. Другими словами, полный резерв времени равен резерву максимального из путей, проходящих через данную работу t.

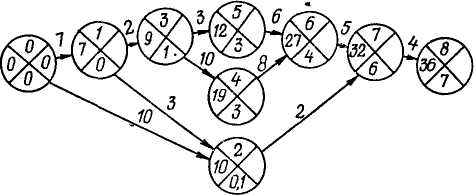
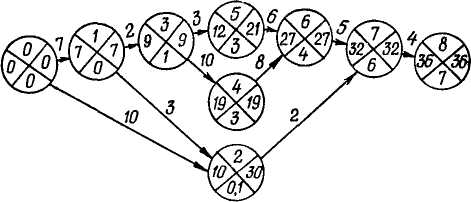
Рис. 41. К примеру вычисления параметров.

Например, если через работу (4,5) проходит два пути 1—4— 5—7 и 1—3—4—5—7, для них соответственно t (1, 4, 5, 7) = 5 и t (1, 3, 4, 5, 7) = 12. Для второго максимального пути резерв времени будет равен 16—12 = 4.

Для простых сетей вместо расчетов параметров по приведен­ным выше формулам можно применить более наглядные и про­стые приемы (вычисление непосредственно на сетевом графике, табличный метод, матричный метод и др.). Рассмотрим кон­кретный пример вычисления параметров непосредственно на се­тевом графике. Суть этого приема состоит в следующем. Каждый кружок, соответствующий определенному событию, делится на четыре сектора (рис. 41, а). В верхних секторах записываются номера события, в левом — вычисленные ранние сроки сверше­ния события Т_р, в нижнем — номер события, через которое к данному событию проходит максимальный по продолжительно-

сти путь и в правом — вычисленные поздние сроки свершения события Т_п.

Рассмотрим ход вычислений. После того как поставлены но­мера событий в верхних секторах, заполняются левые сектора (рис. 41, б), В исходном событии проставляется нуль. Далее рас­сматривается первое событие, в которое входит работа (0, 1). Чтобы получить Т_р, необходимо сложить число 0 с числом 7 (to, i). Результат Т_р = 0 + 7 = 7 запишем в левый сектор события /. Поскольку Т_р достигнуто через событие 0, в нижний сектор за­пишем число 0. В событие 2 входит две работы (1, 2 и 0, 2). Для этого события обе суммы (T_pt + Л, 2) и (Т_ро -f to, 2) равны 10, поэтому в левом секторе запишем 10, а в нижнем — цифры 0 и 1. Аналогично заполняем все секторы кружков остальных событий. В событии 8 — последнем Т_р8 = 36.

При вычислении поздних сроков свершения событий Т_п дви­гаемся в обратном порядке. В правом секторе события 8 ставим цифру 36, так как поздний срок свершения события равен ран­нему сроку. Для события 7 Т_п7 — Т_п8 — h, а = 36 — 4 =- 32. Для события 6 Тпб = Т_п7 — U, 7 — 32 — 5 = 27 и т. д.

Если из события исходит две работы, то определяются две разности и выбирается меньшая. Например, для события 3 Т_пз= = Т_П4 — /з, 4 «= 19 — 10 = 9 и Тпз = Т_п5 — h, 5 = 21 — 3 = 18. Вы­бираем 9 и проставляем в правом секторе события 3.

Чтобы определить резерв времени данного события, необхо­димо из числа в правом секторе вычесть число в левом секторе.

Полный резерв работы можно установить, если из числа в правом секторе конечного события 8 вычесть число левого сек­тора начального события и продолжительность работы между начальным событием и конечным. Например: 36—0— (10 + 2 + + 4)= 20.

При анализе сетевого графика ставится цель выявить возмож­ность сокращения сроков запланированного комплекса работ и загрузки исполнителей работ. При оптимизации графиков ис­пользуются резервы времени. По величинам резервов осуще­ствляется контроль очередности выполненных работ, сокраща­ется длина критического пути и выравнивается продолжитель­ность всех полных путей сети.

Оптимизация может быть частной и комплексной. В случае частной оптимизации минимизируется время выполнения работ при заданной их стоимости или стоимости работ, если задано время. При комплексной оптимизации сетевых графиков нахо­дим оптимум с учетом затрат и сроков выполнения работ. В ос­нову этой оптимизации положен метод время — затраты, суть которого состоит в установлении зависимости между продолжи­тельностью и стоимостью работ.

С помощью сетевых графиков можно управлять процессом выполнения работ. В график вносятся все текущие изменения, возникающие в процессе выполнения работ. Поэтому сетевые

графики являются динамическими моделями. В процессе опера­тивного управления осуществляется контроль за фактическим ходом работ, выявляются отклонения от ранее запланированных работ, принимаются соответствующие решения, направленные на обеспечение выполнения плана работ. Для анализа, оптими­зации и управления сложными сетевыми графиками (более 400—500 работ) следует применять ЭВМ.

Программно-целевое планирование и управление. Одна из важных задач десятой пятилетки в области совершенствования

управления народным хозяйст­вом — широкое использование в планировании программно-целевого метода и разработка комплексных программ по наиболее важным научно-техническим, экономическим и социальным проблемам.

Программно-целевой (целепро-граммный) метод является дальней­шим развитием балансового метода планирования и ""базируется на чет­ком формулировании целей эконо­мического развития, их дальнейшем делении на подцели и выявлении необходимых ресурсов для реали­зации поставленной задачи. Для этого используется аппарат теории графов при построении «дерева целей» и «дерева ресурсов». Дерево — своеобразная схема, показывающая взаимосвязь и соподчинение целей и ре­сурсов (рис. 42), это универсальная структурная модель раз­личных физических систем. Корень дерева является собственно (целостной) системой. Подсистемы первого и последующих уровней можно также рассматривать как целостные системы. Например, Министерства автомобильного транспорта респуб­лики можно расчленить на такие целостные системы: областные производственные управления, автообъединения, автопредприя­тия и т. д.

При расчетах и анализе определяются ключевые (генераль­ные) проблемы, для решения которых должны направляться основные силы и средства. Программно-целевые методы могут успешно применяться не только для перспективного народнохо­зяйственного (макропланирования), но и для отраслевого, ве­домственного и внутрихозяйственного планирования. Примером применения программно-целевого планирования для решения крупной народнохозяйственной проблемы является знаменитый план ГОЭЛРО.

Разработка программы начинается с построения ее целей и подцелей. Дерево целей, направленное, например, на повышение эффективности работы автомобильного транспорта, может вклю-

Рис. 43, Струкгура программной матрицы.

чать такие подцели первого уровня, как «повышение производи­тельности автомобилей» ..., «снижение себестоимости перевозок» ... и «повышение безопасности движения». На втором уровне первая подцель подразделяется на «повышение скоростей движе-

ния», «увеличение грузоподъемности автомобилей» и «сокраще­ние времени простоя под погрузкой — разгрузкой». На третьем уровне подцель «повышения скоростей движения» делится на серию других целей: «тип и конструкция автомобиля», «дорож­ные условия», «квалификация водителя» и т. д. Дерево ресур­сов представляет иерархически построенный граф, показываю­щий ресурсные возможности (наличие подвижного состава, до­рог и подъездных путей, квалифицированных водителей, погру-зочно-разгрузочных механизмов и т. д.) или затраты, необходи­мые на реализацию данной программы.

Наличие реально составленных дерева целей и дерева ресур­сов позволяет осуществлять необходимые анализы и вычисле­ния, в результате которых находятся генеральные программы в виде переходных (соединяющих) звеньев (срастающихся крон деревьев). Выбор того или другого варианта программы осуще­ствляется по разным критериям, которые зависят от содержания программы и ее важности с позиций целей плана. В качестве критериев могут быть минимум времени выполнения программы при данных ресурсных возможностях или минимум затрат на выполнение программы при фиксированных показателях про­граммы и ее времени выполнения. Одним из методических прие­мов, позволяющих взаимоувязывать цель (программы, подпро­граммы) и ресурсы, проводить анализ и выбор эффективных ва­риантов, является программная матрица (рис. 43) *. В качестве примера с условными цифрами показана матрица, которая вклю­чает четыре раздела: раздел П—затраты на объединение под­программ в программу (реализацию программы в целом), раздел А —затраты на объединение элементов в подпрограммы (стоимость подпрограмм), раздел В — затраты на создание всех элементов В\ — В^ (стоимость элементов). Заполнение матрицы начинают с раздела С (затраты ресурсов). Затраты ресурсов указывают на пересечениях строк раздела С со столбцами мат­рицы.

В настоящее время разрабатываются новые весьма перспек­тивные системы, позволяющие человеку вести диалог («собесе­дование») с электронно-вычислительной машиной. Эти системы называются «диспланами» и в ближайшее время будут приме­няться для планирования на различных уровнях. Такие системы особенно полезны при программно-целевом планировании и уп­равлении, когда требуется всесторонний анализ целого комплек­са вопросов, начиная с идеи и кончая решением определенной народнохозяйственной задачи. С помощью «дисплана» представ­ляется возможным специалисту очень быстро проанализировать самые перспективные варианты и корректировать план в про­цессе его создания.

* Математика и кибернетика в экономике. Словарь-справочник. М., «Эко­номика:», 1975. 448 с.

₄

РОЛЬ И МЕСТО ЧЕЛОВЕКА В СИСТЕМЕ УПРАВЛЕНИЯ