₃

ОСНОВЫ ТЕОРИИ ПРИНЯТИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ

§ 1. Основные понятия и общая постановка задач исследования операций

В последние годы во многих областях человеческой деятель* ности успешно применяется сравнительно молодой раздел при* кладной математики, который получил название «исследование операций». Этот раздел часто называется «экономико-матема­тическим методом» или математической теорией принятия опти­мальных решений. Исследование операций находит широкое применение и на автомобильном транспорте. Такой математи­ческий аппарат можно использовать при решении многих транс­портных задач, задач теории массового обслуживания и сете­вого планирования.

Под операцией обычно подразумевается любое мероприятие или система мероприятий, объединенных единым условием (за­мыслом) и направленных к достижению определенной цели. Наука об исследовании операций занимается количественным обоснованием решений во всех областях человеческой деятель­ности. Рассматриваются основные понятия и методические принципы исследования операций, математические методы опти­мизации, методы математического моделирования операций и сетевого планирования. Планирование операций начинается с оценки параметров и заканчивается вычислением значений вероятностей тех или иных событий.

Руководство (управление) операцией складывается из ком-" плексного воздействия на людей в процессе функционирования системы (административные, экономические, правовые, социо­логические, психологические и другие методы), организации структуры и управления операцией, базирующегося на плани­ровании (исследовании) операции и оперативного управления (рис. 8). Принятие решений не входит в задачу исследования операций. Окончательное решение принимает руководитель предприятия, который может располагать данными, не учтен­ными при расчетах. Планирование операций оказывает помощь руководителю в принятии окончательного решения и выступает в роли «советчика». Исследование операций опирается на экспе­римент и индукцию (способ рассуждений от частных фактов и положений к общим выводам). Знание только некоторых фактов позволяет отыскивать новые способы решений и делать

41

важные выводы с помощью эмпирических методов. Можно осу­ществлять сравнение возможных путей управления, находить их характерные особенности, определять количественно их пара­метры, формулировать задачу прогнозирования и устанавли­вать поведение системы при выборе того или иного способа управления.

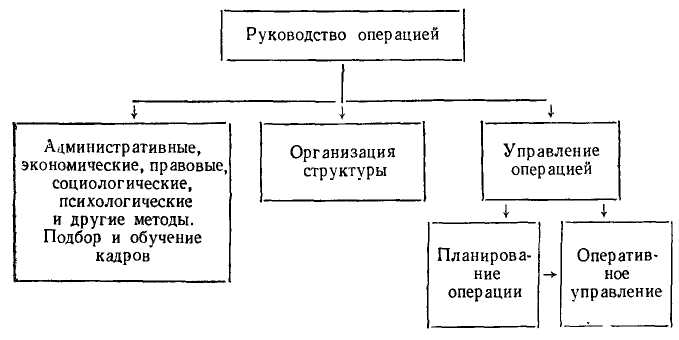
Рис. 8. Схема руководства операцией.

Планирование операций на автомобильном транспорте (рис. 9) представляет собой приложение различных научных приемов и методов, известных из теории эксплуатации автомо­билей, математической статистики, теории вероятностей и т. д., к задачам автомобильного транспорта, позволяющих находить оптимальные решения. Исследование операций применительно к автомобильному транспорту еще не достигло должного уровня.

В задачах по исследованию операций рассматриваются детерминированные, вероятностные и индетерминированные си­стемы. К детерминированным относятся также системы, в кото­рых процессы взаимосвязаны так, что можно проследить цепь причин и следствий (например, системы автоматического управ­ления). Детерминированные системы в статическом состоянии описываются алгебраическими, а в динамическом — дифферен­циальными или интегральными уравнениями. К вероятностным (стохастическим) относятся системы, в которых нет четкого соотношения между входами и выходами и можно установить некоторые вероятностные соотношения с применением матема­тического аппарата теории вероятностей, теории надежности, теории массового обслуживания и т. п. Индетерминированными системами считаются такие, которые состоят из детерминиро­ванных подсистем со случайными связями между ними (напри-

мер, движущийся автомобиль по дороге со случайным харак­тером расположения неровностей).

Применительно к автомобильному транспорту, который мож­но рассматривать как детерминированную, вероятностную или индетерминированную систему, можно привести ряд примеров задач исследования операций.

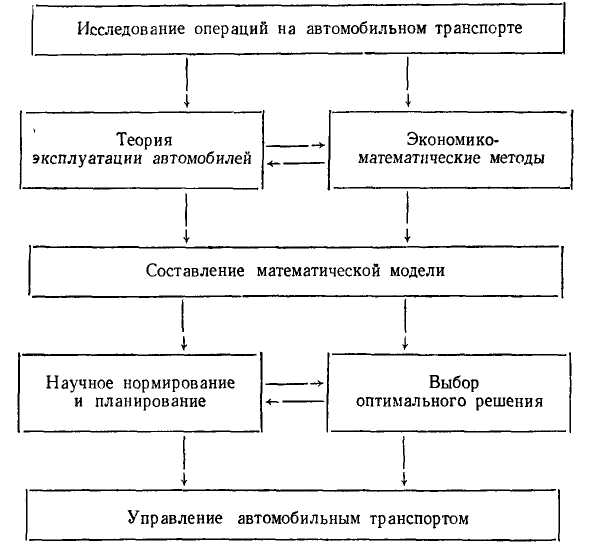
Рис. 9. Схема управления автомобильным транспортом.

Пример 1. В сельскохозяйственном районе следует организовать сезон­ную перевозку сахарной свеклы с полей колхозов и совхозов на свеклопри­емочные пункты определенным количеством и типом подвижного состава. Необходимо выбрать последовательность перевозок, рациональные маршруты перевозок, режим работы автомобилей и водителей, количество автомобилей на каждом маршруте, метод погрузки и разгрузки свеклы и т. д., чтобы обеспечить кратчайшие сроки перевозок груза при заданных транспортных расходах.

Пример 2. В промышленном городе следует организовать перевозку рабо­чих и служащих определенным количеством имеющихся транспортных средств (автобусов и прицепов). Необходимо решить, какие лучше выбрать маршруты движения и стоянки, какое количество и какие автобусы должны работать на каждом маршруте, как должна меняться частота движения автобусов в течение суток и т. д., чтобы обеспечить быструю (своевременную) и ком­фортабельную доставку рабочих и служащих к промышленным предприятиям с учетом случайного характера изменения пассажиропотоков во времени.

Пример 3. В крупном населенном пункте создается сеть станций техни­ческого обслуживания определенного количества автомобилей. Необходимо

выбрать число станций, их размещение, число постоз для технического обслу­живания и текущего ремонта, количество рабочих и т. д., чтобы обеспечить максимальную эффективность их работы.

Во всех приведенных примерах, несмотря на их значитель­ные отличия, есть много общего в самой постановке задачи: имеются конкретные мероприятия (перевозка сахарной свеклы, пассажирские перевозки рабочих и служащих, техническое об­служивание и ремонт автомобилей), преследующие определен­ную цель (минимальные сроки перевозок при заданных мини­мальных транспортных расходах, своевременная и комфорта­бельная доставка рабочих и служащих, максимальная эффек­тивность работы станции технического обслуживания) и задан­ные конкретные условия, характеризующие обстановку данного мероприятия (определенное количество автомобилей, сумма выделенных средств, количество оборудования и технического персонала). Исходя из поставленных условий, необходимо найти количественное обоснование наиболее предпочтительного или оптимального решения. В этом и состоит основная задача иссле­дования операций.

Уровень организации операций должен оцениваться ее эффективностью, т. е. степенью соответствия операции тем тре­бованиям, которые к ней предъявляются. Для количественной оценки эффективности операций введены показатели эффектив­ности (целевые функции, критерии оценки), которые зависят прежде всего от характерных особенностей операций. Показа­телем может быть прибыль, производительность, себестоимость, минимальные затраты, минимальное время движения, вероят­ность нахождения автомобилей в технически исправном состоя­нии и др.

Каждый показатель (критерий) должен отвечать следующим требованиям: быть представительным по отношению к основной задаче функционирования системы, критичным к исследуемым параметрам, достаточно простым и включать в себя результаты всех основных процессов анализируемой операции. Желательно, чтобы критерий был единственным, так как при наличии двух и более критериев исследование сильно усложняется или ста­новится невозможным. Очень важным свойством выбранного критерия является критичность, сущность которого состоит в значительных изменениях численных значений критерия при небольших изменениях исследуемых параметров. Поскольку в исследовании операций рассматриваются случайные процессы, критерий обычно является случайной величиной. В связи с этим, как правило, определяют математическое ожидание критерия и ищут его минимум или максимум. Оптимальным решением считается такое, при котором обеспечивается выполнение по­ставленной задачи при минимуме материальных затрат или, наоборот, обеспечивается максимум эффективности при фик­сированных материальных затратах (обратная постановка за-

дачи). В обшем виде критерий К является математическим ожиданием материальных затрат (стоимости) при заданной (допустимой) эффективности (Э_доп):

При обратной постановке задачи критерием будет эффектив­ность Э при заданных (допустимых) материальных затратах, т. е.

Обе постановки задачи являются равноценными.

В задачах управления часто приходится учитывать не один критерий, а несколько. Эти критерии могут противоречить друг другу. Например, стремление к повышению коэффициента техни­ческой готовности парка автомобилей ведет к увеличению затрат на поддержание его в технически исправном состоянии. Если рассматривать одновременно два, три критерия и более, можно поступить следующим образом. Выбираем один из основных кри­териев, а для других устанавливаем определенные ограничения (пороговые значения) и решаем несколько задач оптимизации по разным критериям при разных пороговых значениях для других критериев. Можно и по другому решать такую задачу. В этом случае определяем смешанный критерий как линейную функцию от других критериев Ai, A₂, .. ., А„. В зависимости от важности критериев вводим разные весовые коэффициенты ai, а₂, ..., а„. В общем смешанный критерий определяется по выражению

Так, обобщающий показатель качества

изделий рекомендуется рассчитывать по формуле [12]

1 г 1 Г\1

где А — комплексный технико-экономический показатель; П_т — технический показатель; П_о — показатель уровня стандартизации; Пппз — показатель патентно-правовой защиты; П_эст — показатель технической эстетики; К\ — Кь — коэффициенты весомости частных показателей в обобщенном показателе качества.

Каждый из частных показателей, в свою очередь, рассчиты­вается по специальным формулам.

Самой важной и сложной задачей является определение коэффициентов весомости. Сделать это обычными математиче­скими методами нельзя. Они обычно устанавливаются путем опроса специалистов (производственников, эксплуатационников, научных работников). С помощью математических методов об­работки данных опроса находим весомость отдельных коэффи­циентов Разница в ответах, как правило, не превышает 20— 25 '/о от номинального значения коэффициентов весомости. Так,

для определения качества микроавтобуса «РАФ-977Д» произве­ден опрос двадцати специалистов Рижского автобусного завода «РАФ» (руководители завода, конструкторы, технологи, произ­водственники) и четырнадцати работников Рижского автоуправ-лепия Минавтошосдора Латвийской ССР. По комплексному технико-экономическому и техническому показателю величины весомости в обобщенном показателе качества микроавтобуса составляют для завода «РАФ» — 33,7 и 24,2%, для автоуправ­ления — 35,4 и 23,5%.

Известны и другие предложения для оценки качества про­мышленных изделий. Например, комплексный показатель качества предложено определять как среднюю геометрическую величину

3

[12]: К = У"ТЭП, где Т — сводный показатель конструктивно-тех­нических средств; Э—сводный экономический показатель произ­водственных затрат; П — сводный показатель потребительских качеств (красота, отделка, удобство пользования).

При любых количественных методах исследования необхо­димо прежде всего построить математическую модель явления. Модель должна быть достаточно полной и простой и учитывать основные факторы, влияющие на конечный исход операции. Решение задач исследования операций как управляемых меро­приятий сводится к нахождению максимума (или минимума) показателя эффективности (целевой функции) путем соответст­вующего выбора зависящих от нас параметров. При этом пред­полагаем, что математическая модель операции построена и можно вычислить показатель эффективности.