Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Российская академия народного хозяйства и государственной службы при президенте российской федерации орловский филиал

ФАКУЛЬТЕТ «Социальные технологии»

КАФЕДРА «Математика и математические методы в управлении»

Типовой расчет

по учебной дисциплине «Математика»

ТЕМА: «Основы теории вероятностей»

Вариант №

Выполнил(а): студент группы 26 ТОСП

Иванов И.И.

Проверила: старший преподаватель

Абрамова Г.Н.

Орел – 2012

Цели и задачи типового расчета

Закрепление знаний, полученных на лекциях по теории вероятности, путем решения типовых задач. Усвоение понятий основных видов случайных событий и отработка навыков алгебраических действий над событиями.

Основные положения теории вероятностей изложены в учебниках:

[1] Н.Ш.Кремер Теория вероятностей и математическая статистика. - М. ЮНИТИ, 2002.

[2] М.С. Красс, Б.П. Чупрынов. Основы математики и ее приложения в экономическом образовании. —М., «Дело», 2003.

[3] В.Е.Гмурман. Теория вероятностей и математическая статистика. - М. Высшая школа, 2000.

Типовой расчет "Теория вероятностей" включает в себя 5 типовых задач, исходные данные для которых задаются для каждого варианта индивидуально. Варианты задаются преподавателем.

1. Классическое определение вероятности.

Задача 1. Имеются изделия четырех сортов, причем число изделий 1-го сорта равно n₁, число изделий 2-го сорта равно n₂, 3-го сорта- n₃, а 4-го сорта- n₄ . Для контроля наудачу берутся m изделий. Определить вероятность того, что среди них m₁ первосортных, m₂, m₃ и m₄ – второго, третьего и четвертого сорта соответственно.

Решение (для нулевого варианта: n₁ =2, n₂ =3, n₃ =1, n₄ =3, m₁ =2, m₂ =1, m₃=0, m₄ =2 ). В соответствии с классическим определением, вероятность наступления события А находится по формуле: Р(А)=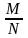 , где N–полное число возможных исходов, а М–число исходов, благоприятствующих событию А. В рассматриваемой задаче полным числом возможных исходов является количество способов, которыми можно из всех n=Σn_i = 9 изделий выбрать m=Σm_i = 5 изделий, причем, порядок выбора не имеет значения. Число таких комбинаций (сочетаний) находится по формуле . N=126.

Количество благоприятствующих исходов находится, как произведение числа способов выбрать требуемое количество изделий каждого сорта. . М=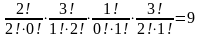

Подставляя полученные значения M и N в формулу, найдем искомую вероятность. Р = 9/126 = 0,71.

Ответ: вероятность того, что из 5 наудачу взятых изделий окажется 2 изделия первого сорта, 1 – второго и 2 – четвертого сорта, равна 0,71.

2. Сумма и произведение событий.

Задача 2. В двух партиях k₁ и k₂ % доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное?

Решение (для нулевого варианта: k₁ =76, k₂ =42). Введем обозначения:

р₁ =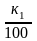 , р₂ = - вероятность выбрать доброкачественное изделие соответственно из первой и второй партии;

событие А — выбрано хотя бы одно бракованное изделие;

событие В — выбраны два бракованных изделия.

событие С — выбраны одно доброкачественное и одно бракованное изделия.

а ). Найдем Р(А). Поскольку выбор изделий из разных партий – события независимые, можно воспользоваться формулой Р(А)= 1 – Р(А), где А – событие, заключающееся в том, что оба изделия доброкачественные.

Р(А) = 1 – р₁∙р₂ =1-0,76∙0,42 =0,68.

б). Найдем Р(В). Поскольку событие В является произведением независимых событий (совместным появлением двух бракованных изделий), и вероятности бракованных изделий в партиях q₁ = 1-p₁ и q₂ = 1-p₂,

Р(В) =(1-p₁)∙(1-p₂ ) = (1-0,76)∙(1-0,42) = 0,14.

в). Найдем Р(С). Событие С является суммой двух несовместных событий: «первое изделие доброкачественное, а второе бракованное» и «первое изделие бракованное, а второе доброкачественное». Каждое из этих событий является произведением соответствующих независимых событий. На основании теорем о сумме несовместных событий и произведении независимых событий можно записать: Р(С) = р_1∙(1-р₂) + (1-р₁)∙р_2.

Р(С) =0,76∙(1-0,42) + (1-0,76)∙0,42 = 0,54

Ответ: Р(А) = 0,68; Р(В) =0,14; Р(С) = 0,54.