1Описание перемещения, скорости и ускорения м.т. в векторной и координатной формах. Средние и мгновенные скорость и ускорение. Вращательное движение. Вектор элементарного углового перемещения. Векторы угловой скорости и углового ускорения. Векторная связь линейной и угловой скорости. Степени свободы твердого тела. Описание поступательного движения т.т. и вращения вокруг неподвижной оси. Плоское движение т.т. Мгновенная ось вращения..

Средняя и мгновееная скорость и ускорение

Вектор мгновенной скорости всегда направлен по касательной к траектории движения точки.

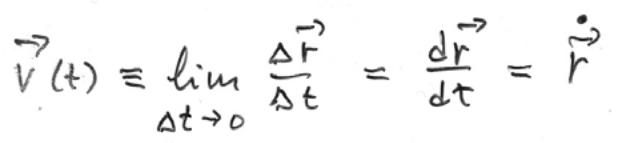
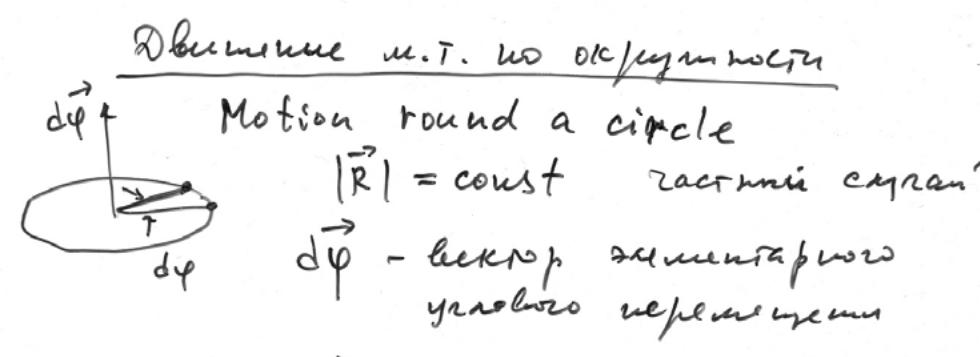
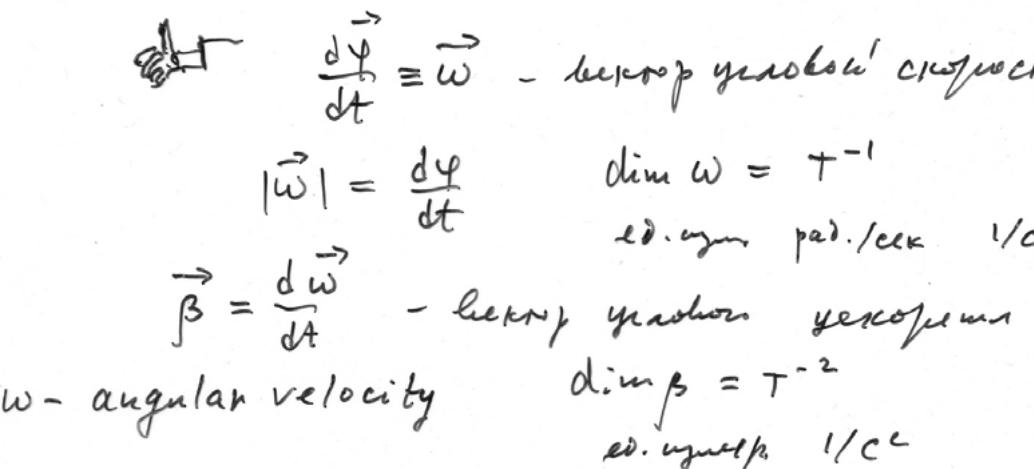
Вращение вокруг неподвижной оси. 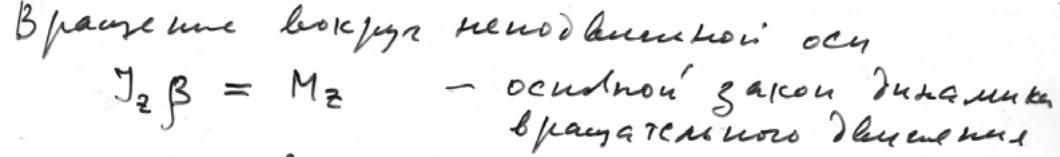Пусть твердое тело, вращаясь вокруг неподвижной в данной системе отсчета оси 00', совершило за время dt бесконечно малый поворот. Соответствующий угол поворота будем характеризовать вектором dip, модуль которого равен углу поворота, а направление совпадает с осью 00', причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора

Теперь найдем элементарное перемещение любой точки А твердого тела при таком повороте. Положение точки А зададим радиусом-вектором г, проведенным из некоторой точки О на оси вращения. Тогда линейное перемещение конца радиуса-вектора г связано с

углом поворота соотношением. Введем векторы угловой скорости и углового ускорения. Вектор угловой скорости со определяют как где At — промежуток времени, за который тело совершает поворот. Вектор со совпадает по направлению с вектором Запишем выражения для угловой скорости и углового ускорения в проекциях на ось вращения z, положительное направление которой свяжем с положительным направлением отсчета координаты ср — угла поворота —правилом правого винта (рис. 1.7). Тогда проекции сог и рг векторов со и р на ось определяются формулами

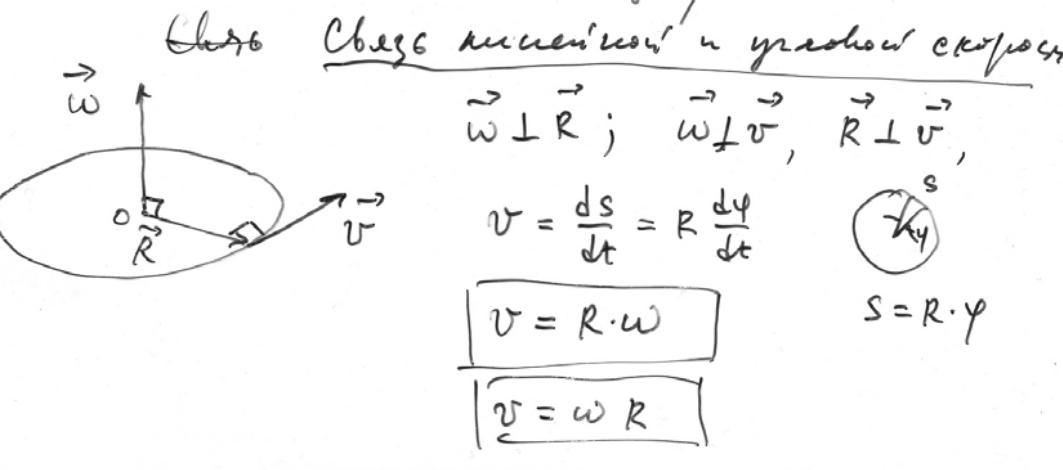
Плоское движение твердого тела. Это такое движение, при котором каждая точка твердого тела движется в плоскости, параллельной некоторой неподвижной (в данной системе отсчета) плоскости.

2 Криволинейное движение. Кривизна траектории. Формулы для тангенциальной и нормальной составляющих вектора полного ускорения. Их характеристика. Законы равнопеременного поступательного и вращательного движений. Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек. Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением При криволинейном движении ускорение можно представить как сумму нормальной  и тангенциальной  составляющих: Прямолинейное движение с постоянным ускорением называется равнопеременным. В зависимости от поведения скорости со временем различают равномерно-ускоренное и равномерно-замедленное движения. Кривизна плоской линии в какой-либо ее точке равна кривизне окружности, сливающейся в данном месте с кривой на бесконечно малом ее участке. Такую окружность называют кругом кривизны плоской линии в данной точке. Центр кривизны всех точек окружности один и тот же и совпадает с центром окружности. Радиус кривизны равен ее радиусу. Прямолинейное движение с постоянным ускорением называется равнопеременным. В зависимости от поведения скорости со временем различают равномерно-ускоренное и равномерно-замедленное движения. Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным. Уравнение равнопеременного вращения φ = φ₀ + ω₀t + εt²/2 и уравнение, выражающее угловую скорость тела в любой момент времени, ω = ω₀ + εt представляют совокупность основных формул вращательного равнопеременного движения тела.

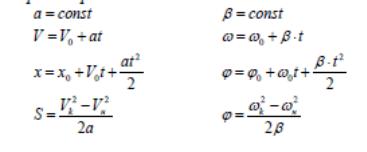
3. Принцип инерции и инерциальные системы отсчета. Принцип относительности. Гипотезы и преобразования Галилея. Классический закон сложения скоростей. Инварианты преобразований Галилея. Инерциальные системы отсчета – с.о., относительно которых выполняется закон инерции, т.е. свободное тело движется равномерно и прямолинейно или покоится. Принцип инерции- всякое тело находится в состоянии покоя или движется равномерно и прямолинейно, если на него не действуют внешние силы. Принцип относительности заключается в том, что все физ-кие явления протекают одинаково в инерциальных с.о. при одинаковых начальных условиях. Никакими механическими опытами нельзя установить покоится данная система отсчета или движется .равномерно и прямолинейно. Гипотезы Галилея: 1)время абсолютно: темп хода часов не зависит от их движения. 2)Размеры тел не зависят от их движения.

Преобразования Галилея – совокупность преобразований моментов времени t и координат

x, y, z некоторого события для двух инерциальных систем отсчета:

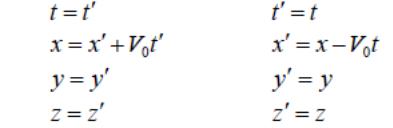
здесь "штрихованная" система отсчета движется поступательно со скоростью 0 V

вдоль оси x лабораторной "нештрихованной" системы отсчета.

Инварианты преобразований – величины, которые не изменяются при данных

преобразованиях. Инвариантами преобразований Галилея, например, являются:

промежуток времени между событиями , размеры тела , ускорение . Инварианты преобразований – величины, которые не изменяются при данных

преобразованиях. Инвариантами преобразований Галилея, например, являются:

промежуток времени между событиями, размеры тела, ускорение. Классический закон сложения скоростей Словами: скорость тела

V относительно лабораторной инерциальной системы отсчета складывается из скорости

0 V движущейся системы отсчета относительно лабораторной и скорости тела

V ′относительно этой движущейся системы.

4Силы и взаимодействия в природе. Масса как мера инертности при поступательном движении тела. Импульс тела. Первый, второй и третий законы Ньютона.

Масса – основная физическая величина, характеризующая инертные свойства тела при

поступательном движении. Сила – векторная физическая величина, количественно характеризующая степень влияния одних тел на другие. Равнодействующая сила – векторная сумма всех сил, действующих на тело. Сила тяжести – сила притяжения тела вблизи поверхности Земли Ускорение свободного падения вблизи поверхности Земли 2и направлено к центру Земли. Сила всемирного тяготения - Это выражение для силы притяжения справедливо для двух шарообразных тел с массами 1 m и 2 m со сферически симметричным распределением плотности. В формуле 12 r - расстояние между центрами шаров. В частности формула справедлива для однородных шаров и точечных масс. Сила упругости – для пружины F = −kx . Сила реакции опоры – сила R действующая на тело со стороны опоры, с которой взаимодействует тело. Сила реакции опоры имеет в общем случае две взаимно перпендикулярные составляющие – силу нормального давления N перпендикулярную поверхности опоры, и силу трения тр F направленную по касательной к поверхности опоры. Сила нормального давления – нормальная составляющая N силы реакции R опоры, действующей на тело. Сила трения покоя – тангенциальная составляющая силы реакции опоры, действующей на тело в отсутствии скольжения тела. Сила трения качения - тангенциальная составляющая силы реакции опоры, действующей на катящееся по опоре тело. Момент силы трения качения относительно центра шара (колеса, цилиндра) пропорционален силе нормального давления: M = r ⋅ N . Сила трения скольжения - тангенциальная составляющая силы реакции опоры, действующей на тело, когда оно скользит по поверхности опоры: F k N Сила вязкого трения (сопротивления) – действует на тело, движущееся в жидкости (газе).Эта сила направлена в сторону противоположную скорости тела относительно среды. При малых скоростях движения сила сопротивления пропорциональна первой степени скорости, а при больших скоростях – второй степени скорости. Сила сопротивления для медленно движущегося в среде шарика – сила Стокса. 1 закон Ньютона: в природе существуют инерциал.с.о. в которых выполняется закон инерции, т.е если тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить его состояние. 2 закон Ньютона: скорость изменения импульса тела равна действующей на тело силе . 3 закон Ньютона: Действие одного тела на другое, т е силы приложенные к телам, равны по величине, но противоположны по направлению и лежат на одной прямой. 5 Импульс системы материальных точек. Вывод уравнения динамики для системы м.т. Центр масс. Уравнение движения центра масс системы материальных точек. Закон сохранения импульса изолированной системы материальных точек. Сохранение отдельных проекций вектора импульса

6Момент импульса материальной точки. Момент силы. Вывод уравнения моментов для материальной точки и системы м.т. Законы сохранения момента импульса изолированной системы материальных точек. Сохранение отдельных проекций вектора момента импульса.

7Работа силы. Потенциальные и непотенциальные силы. Силовое поле. Потенциальная энергия и ее нормировка. Примеры для упругой силы и силы тяжести Земли. Кинетическая энергия. Ее изменение. Закон сохранения механической энергии в нерелятивистском случае.

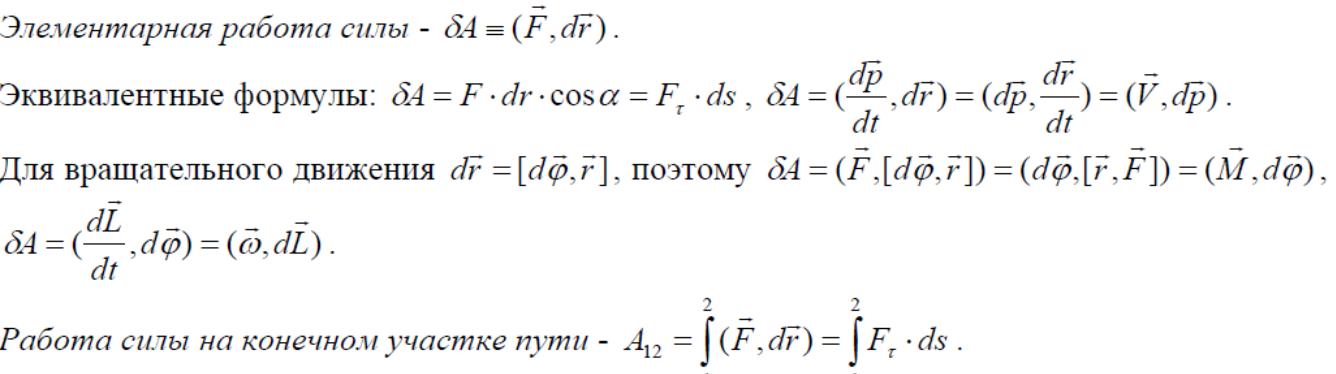
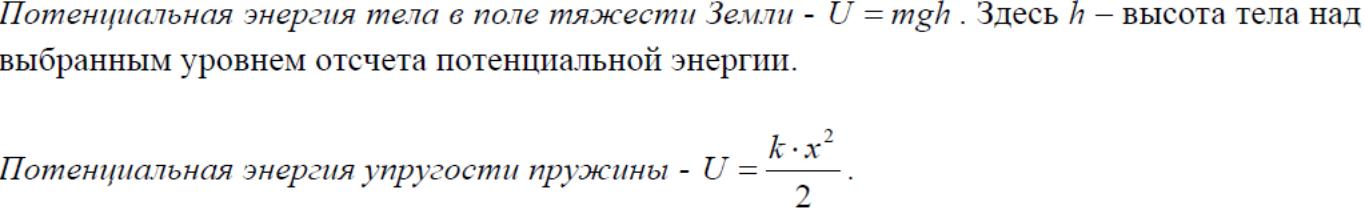
полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной.