26.Бір фазалы синусоидалы ток тізбегі.Синусоидалы эқк,кернеудің ж/е токтардың максималды,әрекет ж/е орташа мәндері.

Бір фазалық синусоидалық токтың тармақталған тізбектеріндегі есептеуді 1-суретте көрсетілген схема мысал.қарастырайық.

Синусоидалы токты тізбектерді есептеумен байланысты сұрақты қарастырайық.Дифференциалдық ж/е символикалық жазбалар түрлерін қолданып, Кирхгоф заңдарының негізінде схеманың барлық тармақтарындағы токтарды есептеу үшін теңдеулер құру.

Тармақтардағы тоқтардын бағытын кез-келген бағытпен аламыз.Дифференциалдық түрде,яғни токтар мен кернеулердің лездік мәндері үшін теідеулер қарастырайық.Кирхгоф 1 заңы бойынша түйінге сәйкес тармақтардағы лездік токтардын алгебралық қосындысы 0- ге тең.Схемада 2 түйін,сол себептен Кирхгофтын 1заңы бойынша бір теңдеу кұраймыз.Кирхгофтын 2заңы бойынша схеманың тұйықталған контурындағы барлық кернеу көздерінің лездік кернеулерінің алгебралық қосындысына тең.Схемада екі тәуелсіз контур,сол себептен Кирхгофтың 2 заңы бойынша екі теңдеу құраймыз.Сонымен,Кирхгоф заңдары бойынша құралған дифференциалдық түрдегі теңдеулер жүйесін аламыз. i1+i2-i3=0 R1i1+L1*di/dt-R2i2=-e2 R2i2+L3*di/dt+1/C3*∫i3dt=e2+e3 Теңдеулерді символикалық түрде жазу үшінтоктардың,ЭҚК-дің,кернеулердің лездік мәндерін комплекс бейнелерімен алмастыру қажет.Сонда,Кирхгофтың заңдары бойынша жазылған символ.түрдегі жүйесін аламыз: I1+I2-I3=0 I1(R1+jXL1)-R2I2=E2 R2I2+I3(jXL3-jXC3)=E2+E3 Алынған теңдеулер жүйесінің шешімі тармақтардағы тоқтардың комплекстік әсер етуші мәндерін анықтауға мүмкіндік береді.

27. Бірфазалы синусоидалы ток тізбектері. Негізгі параметрлерінің анықтамалары, өрнектері. Синусоидалы деп sin заңы б/ша өзгеретін ж/е уақыт б/ша өзгер-н токты айт-з. Синусоидалық токтың лездік мәні мына өрнек-н анық-ды:i=I_msin(2πt/T+ψ)= I_msin(ωt+ψ), мұнд I_m –ток амплитудасы, яғни токтың ең үлкен мәні; синус аргументі 2πt/T+ψ–фаза д.а. Бұрыш ψ-бастапқы уақыт мезгіліндегі (t=0) фазасына тең, сонд-н оны бастапқы фаза д.а.Синусоидалы ток тізб-ң элемент-і:1.активті кедергі R;Бұл токтың лездік кернеуі u=U_msinωt.Ом заңы б/ша u=iR=I_mRsin ωt; Тұж-а: активті кедергіде ток пен кернеу фаза б/ша сәйкес келеді.активті кедергіге келіп түсетін қуат келесі өрнекпен анықт-ы: P=ui=U_msinωtI_msinωt=UIsin²ωt=U_mI_m(1-cos2ωt)/2. Син-ы ток тізб-і индуктивтілік: Х_L=ωL=2πfL; U_L=LdI/dt кернеу-ң лездік мәні. Индуктивтіліктегі кернеу векторы ток векторынан 90̊ озып отырады. Сыйымдылық кедергі: Х_с=1/ωС; u=1/c ₀ʃ^πίdt. Сыйымд-қ кедергіде ток векторы кернеу вект-н 90̊-қа озады.

30.Үшфазалы тізбектер. Үшфазалы тізбектің үшбұрышша жалғануы.Үшбұрышты жалғану кезінде қорек көзінің бір орамының басын екінші қорек көзінің орамының соңымен жалғастырады. Фазалы орамдарының әр жұбының ортақ нүктелері және қабылдағыштар тармақтарының әр жұбының ортақ нүктелерін сызықты сымдармен жалғастырады. Қабылдағыштары бар жұлдызшаның сәулелері немесе үшбұрыштың тармақтары фазалы кедергілер д.а.(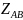 , ,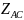 , ,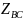 , 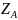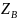). Фазалы орамдарға келтірілетін ЭҚК фазалы ЭҚК д.а(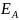 , ,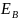 , , , 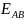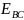).Қорек көздеріндегі кернеулермен токтар-фазалы кернеулер, фазалы токтар д.а. Сызықты сымдар арқылы өтетін токтар мен кернеулер сызықты токтар және сызықты кернеулер д.а. Фазалардың жұлдызшы жалғануы кезінде сызықты токтар фазалы токтарға тең болады = , = , = . 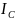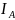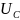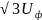Фазалардың үшбұрышты жалғануы кезінде фазалы кернеулер сызықты кернеулерге тең болады. = , = , = .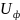