7. Массообменные процесы

7.1. Основы массопередачи

Движущая сила массообменных процессов. Различные вещества могут находиться в различных фазовых состояниях. Например, вода может представлять собой твердую фазу — лед. При обычном давлении и температуре выше вода — жидкость. При высокой температуре вода обращается в пар — паровую фазу. Газы — сильно перегретые пары соответствующих веществ. Различные фазы могут вступать во взаимодействие друг с другом. При этом взаимодействии происходит обмен веществами, растворенными в фазах.

Когда стружку — мелко изрезанную сахарную свеклу — промывают, сахар, содержащийся в клеточной жидкости, переходит в воду. Этот переход обусловлен разностью концентрации сахара в клеточной жидкости и воде. Скорость перехода сахара из стружки в воду будет падать по мере увеличения концентрации сахара в воде и уменьшения его концентрации в стружке. Наконец, эти концентрации станут равными и процесс прекратится.

Движущая сила массообменных процессов — разность концентраций.

При растворении сахара в воде вещество — сахар — переходит из твердой фазы в жидкую. При очистке жидкостей или газов с помощью активированного угля вещество переходит из жидкой или газовой фазы в твердую. При разбавлении растворов вещество переходит из одной жидкой фазы в другую.

Основное уравнение массопередачи. Коэффициент массопередачи. Процесс переноса сахара из стружки в воду в соответствии с основным кинетическим уравнением (1.11) можно описать следующим образом:

(7.1)

или

, (7.2)

где:

— масса вещества, перешедшего из одной фазы в другую, кг; — кинетический коэффициент, учитывающий сопротивление в процессе переноса; — средняя разность концентраций, кг/кг; кмоль/кмоль; кг/м³ и т. д.; — площадь межфазовой поверхности, через которую осуществляется перенос вещества, м²; — продолжительность процесса.

Уравнение (7.2) называют основным уравнением массопередачи.

Коэффициент получил название коэффициента массопередачи.

Размерность его зависит от размерности, принятой для концентрации. Например, если размерность кг/м³, то

.

Физический смысл коэффициента массопередачи следует из его определения:

Коэффициент массопередачи показывает, какое количество вещества переносится через 1 м² поверхности фазового раздела за 1 с при разности концентраций, равной единице.

Коэффициент массопередачи не зависит от площади поверхности, времени и разности концентраций. Он зависит от свойств участвующих в процессе веществ и характера взаимодействия фаз.

Диффузия. Закон Фика. Коэффициент молекулярной диффузии.

Процессы массопередачи называют диффузионными, так как перенос вещества из области с большей концентрацией в область с меньшей осуществляется в результате диффузии.

Представим себе некоторый объем жидкости, покоящийся в сосуде (рис. 7.1), на дне которого лежит растворяемое вещество. Выделим в этом объеме сечение 1, концентрация растворяемого вещества в котором равна и сечение 2 с концентрацией . Если , то вещество в количестве переносится из сечения 1 в сечение 2. Этот перенос в неподвижной жидкости или газе происходит в результате теплового движения молекул. Скорость переноса зависит от скорости и характера молекулярного движения, т. е. от свойств растворенного вещества и растворителя.

Разность концентраций изменяется в рассматриваемом объеме неодинаково по разным направлениям. Наибольшая скорость изменения концентрации наблюдается в направлении нормали и выражается градиентом концентрации:

(7.3)

Знак «минус» в уравнении (7.3) показывает, что вещество переносится в сторону, противоположную направлению градиента концентрации.

Уравнение (7.3) можно переписать по-другому:

. (7.4)

Уравнение (7.4) — отражение закона молекулярной диффузии Фика, который формулируется следующим образом:

Количество вещества, переносимого за счет разности концентраций, прямо пропорционально градиенту концентрации, площади поверхности, через которую происходит перенос, и продолжительности процесса.

Коэффициент в уравнениях (7.3) и (7.4) учитывает свойства среды и переносимого вещества и называется коэффициентом молекулярной диффузии.

Размерность коэффициента молекулярной диффузии зависит от размерности, принятой для измерения концентрации. Например, если концентрацию измерять в кг/м³, то размерность составит:

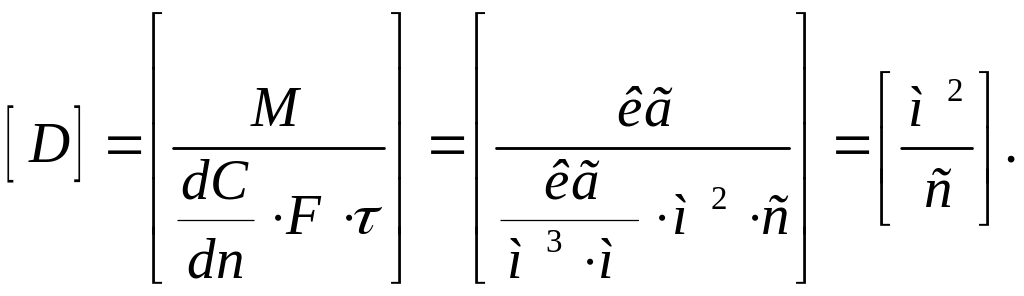
Совпадение размерностей коэффициента молекулярной диффузии , коэффициента температуропроводности и кинематического коэффициента вязкости является случайным и не связано с физическим смыслом этих величин.

Отметим, что закон молекулярной диффузии Фика — аналог закона теплопроводности Фурье.

Конвективный перенос вещества. Из личного опыта каждый знает, что скорость переноса вещества можно значительно увеличить путем перемешивания фаз. Именно так мы поступаем, стремясь побыстрее растворить сахар в стакане чая. При перемешивании к молекулярному диффузионному переносу добавляется очень эффективный перенос вихрями жидкости или газа, образующимися при перемешивании. Такой механизм переноса называют конвективным, а чтобы подчеркнуть диффузионную природу, его называют еще вихревой диффузией.

Вихревая диффузия намного эффективнее молекулярной. Продемонстрируем это на примере.

Возьмем два прозрачных стакана, заполненных водой (рис. 7.2

В каждый стакан бросим несколько кристалликов перманганата калия. Кристаллики упадут на дно, оставив за собой заметный окрашенный след.

Рис.

7.2. Сравнение молекулярной и вихревой диффузии

Теперь с помощью стеклянной палочки перемешаем воду в правом стакане, оставив в покое левый стакан. При перемешивании частицы воды, окружающие кристаллики на дне и уже окрашенные перманганатом калия, переходят вверх, окрашивая остальную воду, а на смену им к кристалликам приходят свежие, еще не окрашенные частицы воды. Движущая сила процесса переноса массы с поверхности кристаллика в воду возрастает, и все повторяется вновь. Можно предположить, что при достаточно интенсивном перемешивании каждая частица воды последовательно побывает у поверхности кристаллика и получит свою долю вещества. Через некоторое время кристаллики полностью растворятся, вода в правом стакане равномерно окрасится и процесс переноса вещества прекратится, так как концентрации в любой точке объема станут одинаковыми. Будет достигнуто состояние равновесия.

В левом стакане за это же время никаких изменений практически не произошло. Окрашен только нижний, прилегающий к кристалликам слой воды. Конечно, через некоторое время и в левом стакане кристаллики полностью растворятся, а жидкость равномерно окрасится. Но для этого потребуется не один десяток часов.

Диаграмма равновесия. Только что мы установили, что процесс переноса вещества прекратится, как только будет достигнута равновесная концентрация в системе. В данном случае после полного растворения кристалликов система состоит из одной фазы и равновесная концентрация установилась в пределах этой фазы. В случае многофазных систем равновесные концентрации в каждой из фаз будут различными, но вполне определенными для каждой фазы в данных условиях. Можно сказать, что при данных температуре и давлении разные фазы обладают различными удерживающими способностями по отношению к одному и тому же веществу.

Рассмотрим равновесие между газовой и жидкой фазами при постоянных температуре и давлении. Пусть — концентрация вещества в газе, а — концентрация этого же вещества в жидкости. Заметим, что если концентрации и измерять одинаковыми единицами и откладывать их на графике в одинаковом масштабе, диаграмма равновесия на рис. 7.3 будет представлять собой квадрат. Если жидкость обладает большей удерживающей способностью, то кривая равновесия расположится ниже диагонали квадрата. Чтобы подчеркнуть, что речь идет о равновесных концентрациях, будем писать индекс «р» — равновесная. Запись означает, что любой концентрации соответствует своя равновесная концентрация , и наоборот.

Достижение межфазного равновесия не следует понимать как прекращение всякого молекулярного движения и связанного с ним переноса вещества. При равновесии количество вещества, переносимого из газовой фазы в жидкую, равно количеству этого вещества, переносимого из жидкой фазы в газовую.

Материальный баланс массообмена. Уравнение рабочей линии. Рассмотрим участок вертикального аппарата, в котором в противотоке взаимодействуют две фазы (рис. 7.4). Пусть жидкая фаза перемещается сверху вниз, изменяя концентрацию поглощаемого вещества от „ в верхнем сечении до в нижнем. Газовая фаза перемещается снизу вверх, изменяя концентрацию от до .

Допустимо предположить, что переход поглощаемого вещества из газа в жидкость ведет к изменению концентрации в фазах, но практически не изменяет расходы жидкого и газового потоков. Поэтому будем полагать, что количество жидкости, входящей в выделенный участок аппарата и выходящей из него, остается постоянным и равным . Также не изменяется количество входящего и выходящего газа.

Количество вещества, которое отдаст газ, определится:

(7.5)

Это же количество вещества поглотит жидкость:

(7.6)

Уравнение материального баланса для выделенного участка аппарата получим, приравнивая правые части уравнений,

(7.7)

Соотношение между количествами взаимодействующих фаз (удельный расход) получим, поделив правую часть уравнения (7.7) на левую:

(7.8)

В пределах рассматриваемого участка между верхним и нижним сечениями произвольно выберем сечение с текущими переменными концентрациями и . Напишем уравнение материального баланса для части аппарата между верхним сечением и сечением .

(7.9)

Решая уравнение (7.9) относительно у, получим

(7.10)

Уравнение (7.10) называют уравнением рабочей линии процесса массообмена. Оно устанавливает зависимость между неравновесными, рабочими концентрациями фаз в любом сечении аппарата.

Перепишем уравнение (7.10), подставив в него значение из уравнения (7.8):

(7.11)

Уравнение (7.11) в координатах представляет собой прямую линию, проходящую через точки ( ) и ( ) на диаграмме равновесия (см. рис. 7.3). В нашем случае рабочая линия расположена выше линии равновесия, так как мы полагали, что вещество переходит из газовой фазы в жидкую.

Особенности массообмена на границе раздела фаз. Процессы массообмена можно разделить на две группы. Первую группу составляют процессы, в которых жидкая фаза взаимодействует с паровой, газовой или другой жидкой фазой. Ко второй группе относятся процессы, в которых присутствует твердая фаза, взаимодействующая с паровой, газовой или жидкой фазой. Процессы переноса для каждой из этих групп существенно различают

Рассмотрим взаимодействие жидкой фазы , перемещающейся сверху вниз, и газовой фазы , перемещающейся снизу вверх (см. рис. 7.4). По аналогии с переносом теплоты можно предполагать, что в результате трения на границе раздела фаз скорость уменьшится, а в жидкости и газе образуются пленки, в которых не будет перемешивания. Эта гипотеза о существовании двух пленок на границе раздела фаз получила название двухплёночной диффузионной модели.

Двухплёночная модель предполагает наличие сопротивления переносу вещества в обеих фазах. В последующем в выражении коэффициента массопередачи мы воспользуемся именно этой моделью. Если предполагать, что в одной из фаз сопротивлением переносу можно пренебречь, можно воспользоваться одноплёночной моделью.

Помимо этих двух сравнительно простых моделей в теории массопередачи используют и другие, более сложные модели, с разной степенью точности удовлетворяющие результатам экспериментальных исследований.

Вернемся к переносу вещества через две пограничные пленки (см. рис. 7.5). Если предположить, что вещество переходит из газа в жидкость, весь процесс переноса можно разделить на четыре этапа.

Первый этап — перенос вещества из ядра газового потока к границе раздела фаз. Если интенсивность перемешивания в ядре потока достаточно высокая, то перенос на первом этапе обеспечивается за счет вихревой диффузии, скорость переноса высокая, а сопротивление незначительно.

Второй этап — перенос вещества через пограничную пленку в газовой фазе за счет молекулярной диффузии.

Третий этап — перенос вещества через пограничную пленку в жидкой фазе за счет молекулярной диффузии.

Четвертый этап — перенос вещества, прошедшего через пограничную пленку, в ядро потока жидкости. Сопротивление переносу на этом этапе зависит от гидродинамических характеристик движения жидкости.

Уточним, что в конечном итоге скорость переноса вещества из фазы в фазу будет определяться наибольшим сопротивлением, возникающим на любом из четырех этапов переноса.

На рис. 7.5 справа условно показаны изменения концентрации распределяемого вещества в фазе от в ядре потока до на границе поверхности раздела фаз. С другой стороны, концентрация в фазе изменяется от на границе поверхности раздела фаз до в ядре потока жидкости. На границе раздела фаз предполагается равновесие, т. е. , а .

Закон массоотдачи Щукарева. По аналогии с законом теплоотдачи Ньютона русским ученым А. Н. Щукаревым был сформулирован закон массоотдачи:

Количество вещества, переходящего из одной фазы в другую прямо

пропорционально разности концентраций в фазе и на границе раздела фаз, площади поверхности контакта фаз и продолжительности процесса.

Для установившегося процесса массоотдачи закон Щукарева можно записать для газовой фазы :

(7.12)

и для жидкой фазы :

, (7.13)

где:

и — коэффициенты массоотдачи в фазах и , соответственно; размерность коэффициентов массоотдачи совпадает с размерностью коэффициента массопередачи (см. подраздел этой главы «Основное уравнение массопередачи. Коэффициент массопередачи») и зависит от размерности, принятой для концентрации.

Выражение коэффициентов массопередачи через коэффициенты массоотдачи. Пусть условия равновесия для процесса на рис. 7.5 слева изображаются прямой линией с угловым коэффициентом , уравнение которого запишется:

. (7.14)

Если предположить, что на границе раздела фаз достигаются условия равновесия, то концентрацию в уравнении (7.14) можно рассматривать как равновесную концентрацию , т. е. условие равновесия в данной точке можно представить уравнением:

. (7.15)

Воспользуемся двумя последними уравнениями и выразим концентрацию в фазе через концентрацию в фазе :

и .

Подставляя концентрации Хр _г и х в уравнение (7.13), получим:

. (7.16) Определим движущую силу из уравнений (7.12) и (7.16):

(7.17)

. (7.18)

Сложив левые и правые части уравнений (7.17) и (7.18), получим:

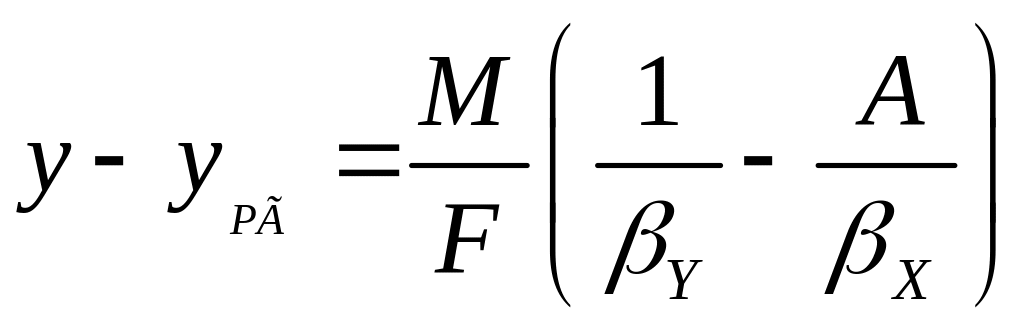. (7.19)

Напишем основное уравнение массопередачи в фазе :

. (7.20)

Решим уравнение (7.20) относительно движущей силы:

. (7.21)

Сравнивая равенства (7.19) и (7.21), приходим к выводу, что:

, (7.22)

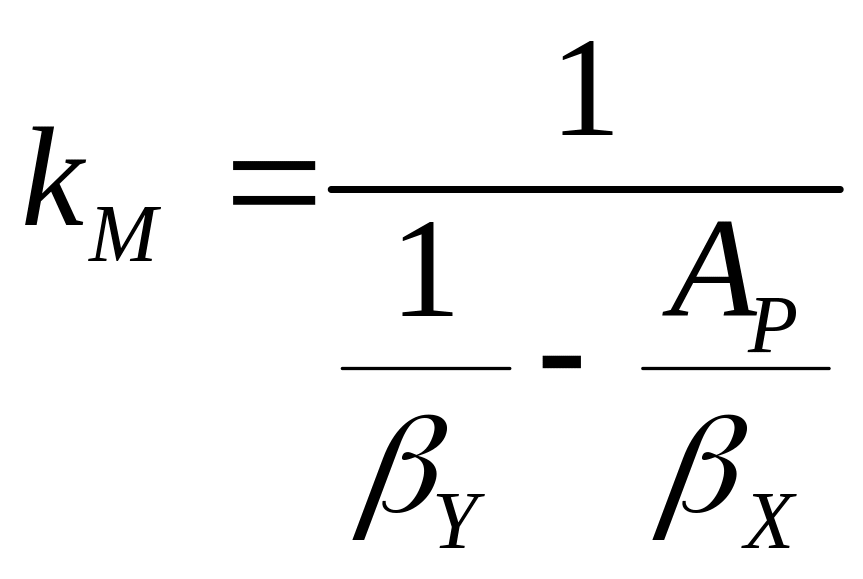. (7.23)

В уравнении (7.23) первое слагаемое знаменателя правой части представляет собой сопротивление переносу в фазе , а второе — сопротивление в фазе . Если коэффициент массоотдачи намного больше коэффициента , то сопротивлением в газовой фазе можно пренебречь и принять

. (7.24)

Если, наоборот, , можно пренебречь сопротивлением в жидкой фазе и тогда .

Сделанные выводы справедливы для случая, когда условия равновесия представлены прямой . Если условия равновесия представлены кривой, то будет изменяться по высоте аппарата. В этом случае аппарат разбивают на участки, для которых кривую равновесия возможно заменить прямой, т. е. полагать и постоянными на каждом участке.

Повторяя проделанный вывод, заменив концентрацию в фазе концентрацией в фазе и подставив и в уравнение (7.13), получим другое выражение для :

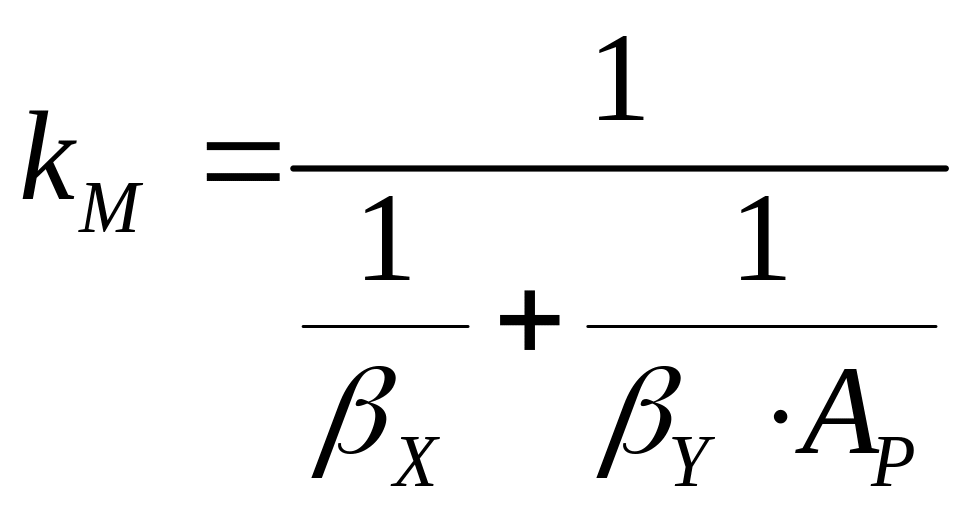. (7.25)

В отличие от коэффициента теплопередачи коэффициент массопередачи имеет два написания. Это связано с возможностью выражения движущей силы через разность концентраций как в одной, так и в другой фазе.

Аналогия в переносе теплоты и массы. Определение коэффициентов массоотдачи. Ранее мы уже ссылались на аналогичность описания процессов тепло- и массоотдачи. Теперь проведем более подробный сравнительный анализ законов, описывающих переносы теплоты и массы, и воспользуемся результатами этого анализа для написания критериальных уравнений массоотдачи.

Сравним основные уравнения тепло- и массопередачи:

и .

Как видим, основные уравнения аналогичны и различаются только движущей силой.

Аналогичны законы теплопроводности и молекулярной диффузии:

и .

Аналогичны законы теплоотдачи и массоотдачи:

и .

Аналогично определяют среднюю движущую силу:

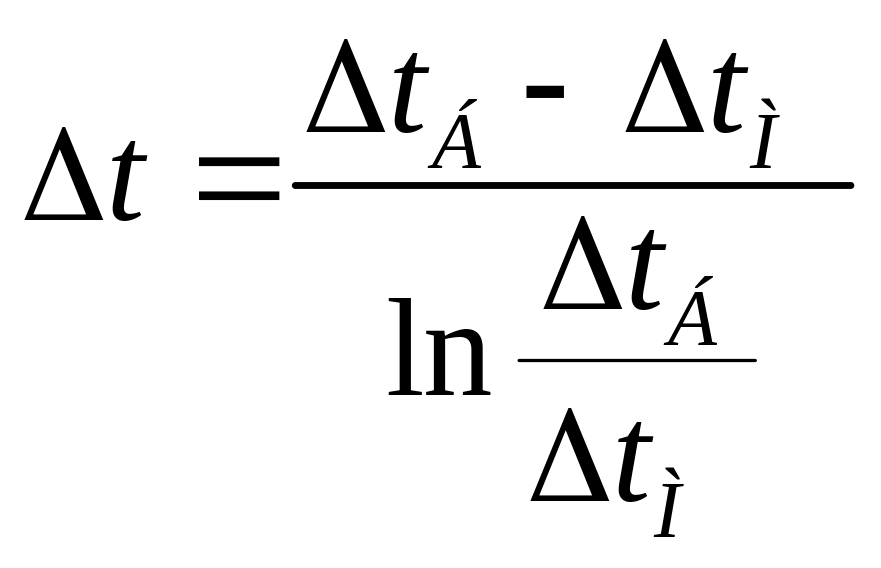и ;

и .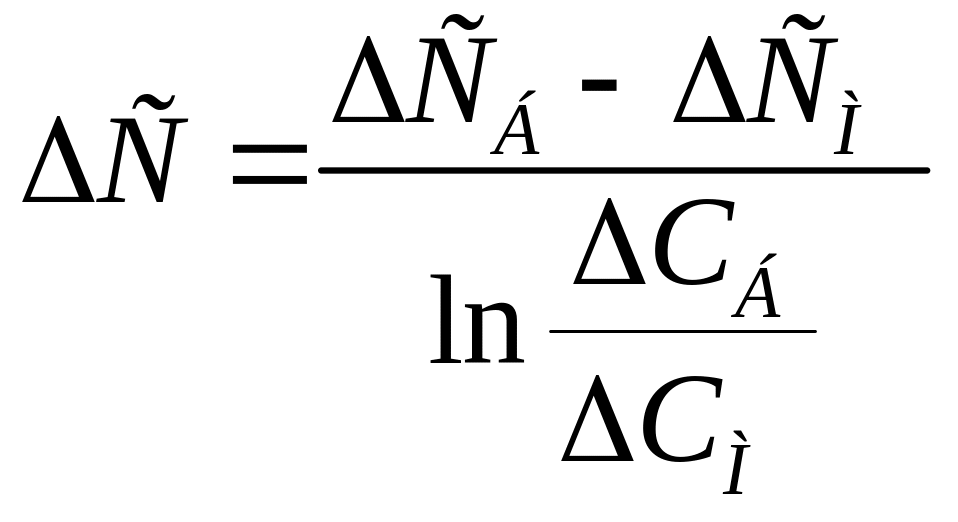

Внешние проявления аналогии опираются на аналогию физических процессов переноса. Воспользуемся аналогией в описании процессов массоотдачи.

Подобно процессу теплоотдачи, где коэффициент теплоотдачи определяется через критерий Нуссельта:

,

коэффициент массоотдачи определяется через диффузионный критерий Нуссельта:

(7.26)

где:

— характерный размер; D — коэффициент молекулярной диффузии.

Диффузионный критерий Нуссельта характеризует массообмен на границе раздела фаз.

Аналогично процессам теплоотдачи критериальное уравнение массоотдачи имеет вид:

. (7.27)

Здесь критерии , и имеют тот же физический смысл, что и в процессах теплоотдачи; — диффузионный критерий Прандтля, характеризует физические свойства веществ, участвующих в процессе:

, (7.28)

где:

— кинематический коэффициент вязкости.

Диффузионный критерий Фурье

, (7.29)

как и аналогичный тепловой критерий, характеризует неустановившиеся процессы массоотдачи.

Как и при теплообмене, симплексы и др. характеризуют геометрическое подобие в системах.

В процессах, где вещество переносится из твердой фазы, используют диффузионный критерий Био:

, (7-30)

где:

— коэффициент массопроводности или коэффициент внутренней диффузии.

Критерий Био — мера сравнения скоростей внешней и внутренней диффузии вещества, извлекаемого из твердой фазы.

Структура потоков и распределение времени пребывания в аппара­те. Модели движения потоков. В современных промышленных аппаратах, иногда имеющих весьма сложную конфигурацию, потоки претерпевают сильную деформацию, в результате которой увеличивается неравномерность распределения скорости по живому сечению потока. Даже при ламинарном движении в трубе скорость жидких частиц в сечении различна и распределяется по параболическому закону [см. уравнение (3.54)]. В центре трубы частицы движутся с наибольшей скоростью, а у стенок — с наименьшей. Следовательно, и в этом простейшем случае время пребывания частиц в трубе неодинаково.

В аппарате, изображенном на рис. 7.6, в «углах» образуются так называемые застойные зоны, время пребывания в которых во много раз может превосходить время, в течение которого через аппарат пройдет основной поток.

Слишком короткое время пребывания одних частиц и чрезмерно продолжительное пребывание других в рабочем объеме ведет к неравномерному нагреву или охлаждению, к неравномерности протекания химических, биохимических и микробиологических превращений. Это не только приводит к снижению качества продукции, но и значительно уменьшает производительность аппарата.

Из-за невозможности рассчитать скорости движения частиц в некоторых частях аппарата распределение частиц потока по времени их пребывания определяют экспериментально. Для этого в поток, поступающий в аппарат, вводят индикатор (красители, соли, радиоактивные вещества) и измеряют его концентрацию в выходящем потоке в течение времени . Полученные результаты представляют в виде кривых , получивших название кривых отклика. Кривые отклика характеризуют распределение частиц по времени их пребывания в аппарате. Полученные таким образом данные используют в технологических расчетах.

Сопоставление и обобщение многочисленных и различных кривых отклика привело к созданию двух теоретических моделей движения потоков: модели идеального вытеснения и модели идеального перемешивания.

Модель идеального вытеснения предполагает, что частицы в каждом сечении потока движутся параллельно друг другу с одинаковой скоростью подобно поршню. Поэтому такое движение потока еще называют поршневым.

В модели идеального вытеснения время пребывания всех частиц в аппарате одинаково и постоянно.

Индикатор, импульсно введенный в начальное сечение потока, через некоторое время целиком окажется в выходном сечении, сохранив свою начальную концентрацию . Это значит, что концентрация его в выходном сечении через время от момента ввода мгновенно возрастает от нуля до (рис. 7.7, а).

Если площадь поперечного сечения аппарата (м²), его высота (м), а постоянная скорость движения частиц (м/с), то время пребывания

. (7.31)

Помножив числитель и знаменатель выражения (7.31) на , получим:

. (7.32)

Время пребывания всех частиц жидкости в аппарате равно отношению рабочего объема аппарата к объемному расходу жидкости .

К модели идеального вытеснения приближается структура потока в аппаратах с длинными трубками небольшого диаметра или в аппаратах, заполненных зернистой насадкой.

Модель идеального перемешивания предполагает, что во всех точках рабочего объема аппарата концентрация индикатора одинакова. Если на входе в аппарат импульсно вводится индикатор, то сразу же в результате совершенного перемешивания концентрация индикатора в выходном сечении, как и в любой точке внутри аппарата, станет равной . Затем концентрация будет уменьшаться, так как происходит вымывание индикатора свежей жидкостью, поступающей в аппарат (рис. 7.7, б).

При расходе поток жидкости за время унесет из аппарата количество индикатора, равное . За это же время количество индикатора в объеме аппарата уменьшится на величину . Приравняем эти количества, учитывая знаком «минус» уменьшение концентрации:

. (7.33) Разделим переменные и получим следующее дифференциальное уравнение:

. (7.34)

Заметим, что среднее время пребывания жидкости в аппарате

.

Перепишем уравнение (7.34) с учетом последнего замечания:

. (7.35)

Проинтегрируем уравнение (7.35) в пределах изменения концентрации от до за время от нуля до , получим:

. (7.36)

По уравнению (7.36) можно рассчитать концентрацию индикатора в любой момент времени и количество индикатора, унесенного из аппарата потоком жидкости за это время. Это уравнение показывает также, что полное вымывание индикатора из рабочего объема аппарата практически невозможно, так как при , как это показано на рис. 7.7, б.

В реальных аппаратах структура потоков не соответствует теоретическим моделям. Жидкость, проходя через аппарат, частично перемешивается в поперечном и продольном направлениях.

Кривая отклика для реальных аппаратов имеет вид кривой на рис. 7.7, в. Индикатор, импульсно введенный на входе потока, появляется на выходе лишь по истечении времени . Концентрация индикатора на выходе постепенно возрастает до , а затем убывает, асимптотически приближаясь к нулю при .

Таким образом, в реальных процессах вначале кривая отклика (левая её часть до ординаты ) как бы напоминает кривую модели идеального вытеснения. Разница состоит в том, что в теоретической модели концентрация мгновенно достигает максимального значения, а в реальной этот процесс растянут по времени от до .

С другой стороны, правая часть реальной кривой отклика напоминает кривую теоретической модели идеального перемешивания.

Для математического описания процессов в многоступенчатых или секционированных аппаратах используют ячеистую модель (рис. 7.7, г). Согласно этой модели аппарат состоит из последовательно работающих ячеек, в каждой из которых достигается идеальное перемешивание. В то же время перемешивания между отдельными ячейками нет.

Среднее время пребывания жидкости в каждой ячейке одинаково и равно . Для произвольно выбранной і-й ячейки концентрация индикатора

(7.37)

Система, составленная из уравнений (7.37), написанных для каждой из ячеек, имеет следующее решение:

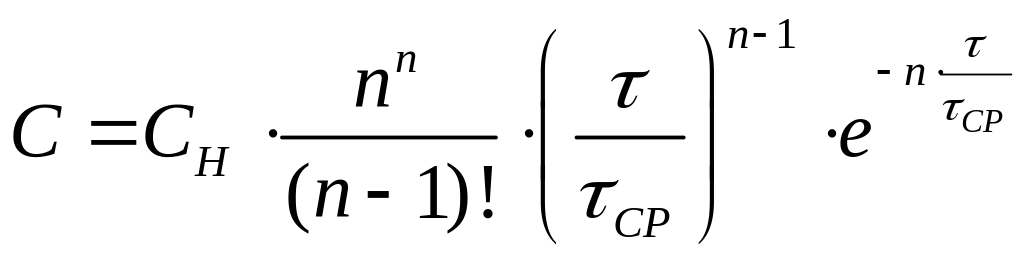. (7.38)

Уравнение (7.38) позволяет определить концентрацию индикатора при импульсном вводе в любой момент времени в любой ячейке.

При ячеистая модель переходит в модель идеального перемешивания, а при — в модель идеального вытеснения.

Для несекционированных аппаратов применяют диффузионную модель. Эта модель полагает, что отклонение распределения времени пребывания частиц от распределения при идеальном вытеснении обусловлено обратным перемешиванием. Учитывая существенное влияние этого явления на перенос, остановимся на нём подробнее.

В противоточном аппарате (см. рис. 7.4) выделим участок между сечениями 1 и 2. Как уже отмечалось, скорость массоотдачи из одной фазы в другую определяется характером движения фаз. Чем выше турбулентность в фазах и на границе раздела фаз, тем выше степень перемешивания и выше скорость переноса.

С другой стороны, сове ршенное перемешивание в выделенном объеме аппарата приведет к выравниванию концентраций, т. е. будет достигнуто равенство:

и .

Другими словами, пройдя между сечениями 1 и 2, ни одна из фаз не изменит своей концентрации, а значит, никакого переноса массы не будет достигнуто. Перенос массы осуществится, если

, и ,

а для этого необходимо ограничить перемешивание в каждой из фаз, т. е. ограничить продольное перемешивание. Имея в виду вихревую и диффузионную природу продольного переноса, его интенсивность оценивают коэффициентом продольного перемешивания . Этот коэффициент входит в критерий Пекле для продольного перемешивания:

. (7.39)

Здесь — средняя скорость потока, м/с; — высота (длина) аппарата, м.

Размерность коэффициента продольного перемешивания совпадает с размерностью коэффициента диффузии.

Критерий — аналог известного диффузионного критерия и теплового критерия . Величина его зависит от конструкции и размеров аппарата, характера взаимодействия фаз и определяется опытным путем. Для модели идеального вытеснения, где продольного перемешивания нет, , а . Для модели идеального перемешивания и .

На практике встречаются случаи, когда ни одна из предложенных здесь моделей не адекватна реальным условиям в аппарате. Поэтому в специальной литературе описаны другие, более сложные модели движения потоков.

Контрольные вопросы и задания. 1. Приведите примеры процессов массопередачи. 2. Почему вещество, распределяемое в жидкой или газовой среде, переходит из области с большей концентрацией в область с меньшей концентрацией? 3. Почему, чтобы растворить сахар в стакане чая, его перемешивают ложечкой? 4. В чем проявляется аналогия в переносах теплоты и массы? Где эта аналогия не соблюдается? 5. От чего зависит скорость процесса массопередачи? 6. От чего зависит величина коэффициента массопередачи? Поясните его физический смысл. 7. Как определяют движущую силу в процессах массопереноса? 8. Как вычисляют коэффициенты массоотдачи? 9. Какая модель движения потока соответствует многоступенчатому процессу?