2. Оптимальное управление портфелем ценных бумаг

2.1. Предварительные понятия

Определение: Стремление разнообразить набор ценных бумаг называется диверсификацией.

Определение: Набор ценных бумаг называется инвестиционным портфелем.

Определение: Наилучший в «смысле» заданного критерия набор ценных бумаг называется оптимальным портфелем.

Определение. Периодом владения (holding period) называется отрезок времени, в течение которого предполагается владеть ценной бумагой.

Определение. Доходность ценной бумаги определяется следующим образом. Пусть ценная бумага i в момент приобретения стоила S_i, а в момент периода владения ценная бумага стоит S_i^’. В течение периода владения по ценной бумаге может быть получен дополнительный доход P_i (например, дивиденды). Доходностью ценной бумаги называется величина .

Доходность ценной бумаги будем рассматривать как случайную величину. Обозначим математическое ожидание этой случайной величины , вторые центральные моменты -

При i = j имеем дисперсию доходности ценной бумаги: .

Построим матрицу: , которая называется ковариационной матрицей доходности.

Для получения оценок величин используют модели рынка ценных бумаг.

Простейшая модель рынка ценных бумаг описывается формулой , где r – случайная величина, называется индексом рынка ценных бумаг, с математическим ожиданием и дисперсией ; - некоторые числа, характеризующие i­-ю ценную бумагу; - независимые случайные величины с нулевыми математическими ожиданиями (то есть ) и дисперсиями .

Предполагается, что величины r и взаимно независимы.

1. Доходность портфеля ценных бумаг. Пусть в начале периода владения портфелем ценных бумаг, портфель стоил W₀ денежных единиц, в конце периода владения портфелем стоит W₁, в течение периода владения получается дополнительный доход P.

Определение: Доходностью портфеля ценных бумаг называется величина .

Покажем, как связаны доходность портфеля и доходность отдельных ценных бумаг. Предположим, что в портфель входит n₁ ценных бумаг № 1, n₂ ценных бумаг № 2, … Тогда .

Введем обозначение: x_i – доля стоимости i-й ценной бумаги в портфеле:

.

Доли удовлетворяют условию нормировки, т.е. . Очевидно,

, .

Тогда

Таким образом, .

Найдем характеристики случайной величины :

;

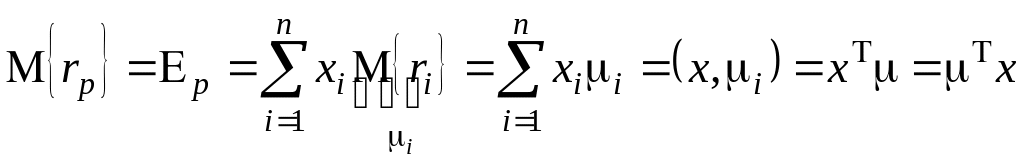Это квадратичная форма, где С – положительно определенная матрица, , .

В дальнейшем используем такие обозначения: - СКО портфеля ценных бумаг.

Пример: Найдем формулы для средней доходности и дисперсии портфеля в случае простейшей модели рынка ценных бумаг, когда

, ,

В этой формуле первое слагаемое называется рыночной компонентой дисперсии портфеля, второе – собственной дисперсией портфеля.

Сводка основных формул

- средняя доходность портфеля

- дисперсия доходности портфеля

- СКО доходности портфеля

, - условие нормировки

2.2. Задача инвестора

Это многокритериальная задача (2 критерия).

Так как критерии являются противоречивыми, то решение находится виде компромисса. Иногда задача решается путем сведения к однокритериальной задаче, т.е. к задаче вида:

Это задача квадратичного программирования.