Пластическая и упругая деформация

В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.

За счет наличия деформационных способностей все известные материалы обладают набором полезных свойств – пластичностью, хрупкостью, упругостью, прочностью и другими. Исследование этих свойств достаточно важная задача, позволяющая выбрать или изготовить необходимый материал. Кроме того, само по себе наличие деформации и его детектирование часто бывает необходимо для задач приборостроения, для этого применяются специальные датчики называемые экстензометрами.

Закон Гука

Закон пропорциональности удлинения пружины приложенной силе был открыт английским физиком Робертом Гуком (1635-1703г.)

Научные интересы Гука были столь широки, что он часто не успевал доводить свои исследования до конца. Это давало повод к острейшим спорам о приоритете в открытии тех или иных законов с крупнейшими учеными ( Гюйгенс, Ньютоном и др.). Однако закон Гука был настолько убедительно обоснован многочисленными экспериментами, что тут приоритет Гука никогда не оспаривался.

Теория пружины Роберта Гука:

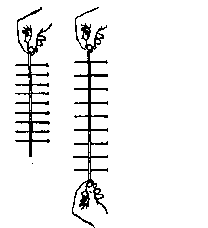
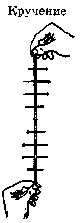
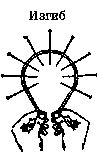
Закон гука

Сила упругости прямо пропорциональна величине деформации.

Закон Гука справедлив при малых ( упругих) деформациях тел.

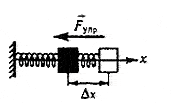
Модуль силы Гука:

F упр = k | x |

где k -коэффициент упругости или жесткость пружины (ед.изм. в СИ - 1 Н/м ) х - удлинение пружины или величина деформации пружины ( ед.изм. в СИ - 1м) Fупр - сила упругости (ед.изм. в СИ - 1Н)

Модуль упругости

МОДУЛИ УПРУГОСТИ(от лат. modulus — мера), величины, характеризующие упругие св-ва материалов при малых деформациях. При растяжении силой F цилиндрич. образца длиной l с площадью поперечного сечения 5 имеет место линейная зависимость между норм. напряжением в поперечном сечении s=F/S и относит. удлинением e=Dl/l, т. <е. s=Еe. Константа материала Е наз. м о д у л е м Ю н г а или м о д у л е м п р о д о л ь н о й у п р у г о с т и. При растяжении относит. уменьшение поперечных размеров образца — e' пропорц. e. Величина v=-e'/e, наз. коэффициентом Пуассона. При крученни тонкостенного трубчатого образца касат. напряжение т в поперечном сечении пропорц. деформации сдвига у, т. е. t=Gg. Константа материала G наз. м о д у л е м с д в и г а. В изотропном материале значения Е, G, v не зависят от направления, в к-ром вырезан из среды испытуемый образец. При сжатии изотропного тела произвольной формы равномерным давлением р в нём возникает однородное гидростатич. напряжённое состояние, при к-ром s11=s22=s33=- р, s12=s23=s31=0 и гидростатич, деформация e11=e22=e33=e, e12=e23=e31=0, причём 3e=q, где q — относит. изменение объёма пропорц. давлению, т. е. - p=Kq или s=3Ke, где s= 1/3(s11+s22+s33) — среднее напряжение. Константа К наз. м о д у л е м о б ъ ё м н о й у п р у г о с т и (иногда — модулем всестороннего сжатия).

В обобщённом Гука законе вводится ещё два М. у.— постоянные Ламе l и m, причём в изотропном материале независимых М. у. только два (напр., l и m или Е и v). Между М. у. имеют место равенства:

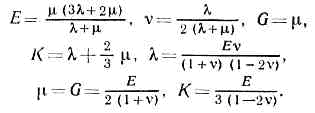
Для большинства металлов v»0,3. Значение v=0,5 соответствует механически несжимаемому материалу. В стали E»2•106 кгс/см2, G»8•105 кгс/см2; в меди E»0,9•106 кгс/см2, G»4•105 кгс/см2; в алюминии E»0,75•106 кгс/см2, G»2,7•105 кгс/см2; в граните E»0,8•106 кгс/см2, G»3•105 кгс/см2.

В анизотропном материале упругие св-ва определяются 21 М. у. В ряде материалов (монокристаллы, направленно армированные композиты и т. <п.) имеются плоскости симметрии упругих св-в. При этом число независимых М. у. уменьшается.

М. у. зависят от темп-ры; на величину М. у. для данного материала влияют: термообработка, радиоактивное облучение, скорость деформации и др. внеш. факторы.

МОДУЛИ УПРУГОСТИ

- величины, характеризующие упругие свойства материала. В случае малых деформаций упругого тела связь между компонентами напряжения s₁₁, s₂₂, ..., s₃₁ и компонентами относит. деформации e₁₁, e₂₂, ... , e₃₁ в нек-рой точке тела представляется шестью линейными соотношениями (см. Гука закон):

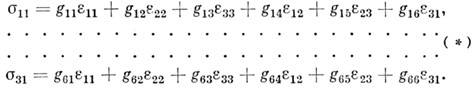
Коэф. g₁₁, g₁₂, ..., g₆₆ наз. М. у. и имеют размерность напряжения, т. е. единицы силы, отнесённой к единице площади, поскольку e_ij - безразмерные величины. Физ. смысл M. у. выявляется при рассмотрении осн. элементарных типов напряжённого состояния упругого тела: одностороннего нормального напряжения, чистого сдвига и всестороннего нормального напряжения. Для каждого из этих напряжённых состояний зависимость между напряжением и соответствующей ему 

деформацией определяется простейшей ф-лой: напряжение равно произведению соответствующей деформации на M. у. Одностороннему нормальному напряжению s, возникающему при простом растяжении (сжатии), соответствует в направлении растяжения модуль продольной упругости E (модуль Юнга). Он равен отношению нормального напряжения к относит. удлинению, вызванному этим напряжением в направлении его действия: E =s/e и характеризует способность материалов сопротивляться деформации растяжения.

Напряжённому состоянию чистого сдвига, при к-ром по двум взаимно ортогональным площадкам действуют только касат. напряжения т, соответствует модуль сдвига G. По величине он равен отношению касат. напряжения т к величине угла сдвига g, определяющего искажение прямого угла между плоскостями, по к-рым действуют касат. напряжения: G= т/g и представляет способность материала сопротивляться изменению формы при сохранении его объёма.

Всестороннему равному нормальному напряжению s, возникающему при гидростатич. давлении, соответствует модуль объёмного сжатия К (объёмный M. у.). Он равен отношению величины нормального напряжения к величине относит. объёмного сжатия, вызванного этим напряжением: К =s/q (где q = e₁₁ + e₂₂ + e₃₃ - относит. изменение объёма) и характеризует способность материала сопротивляться изменению его объёма, не сопровождающемуся изменением формы.

К пост. величинам, характеризующим упругие свойства материала, относится коэф. Пуассона v. Величина его равна отношению абс. значения относит. поперечного сжатия сечения e' (при одностороннем растяжении) к относит. продольному удлинению e, то есть v = |e'|/e. Величины M. у. и коэф. Пуассона для нек-рых материалов приведены в табл. 1. Для однородного изотропного тела, напр. мелкозернистого ме-таллич. поликристалла с беспорядочной ориентировкой зёрен (т. е. не имеющего текстуры), M. у. и коэф. Пуассона одинаковы по всем направлениям. Величины E, G, К и v связаны соотношениями:

Теплоемкость. Теплопроводность и тепловые расширения твердых тел

ТЕПЛОЁМКОСТЬ

количество теплоты, поглощаемой телом при нагревании на 1 градус (1°С или 1К); точнее — отношение кол-ва теплоты, поглощаемой телом при бесконечно малом изменении его темп-ры, к этому изменению. Т. ед. массы в-ва (г, кг) наз. удельной Т., 1 моля в-ва — молярной (мольной) Т. Ед. Т. служат Дж/(кг•К), Дж/(моль•К), Дж/(м3•К) и внесистемная ед. кал/(моль•К).

Кол-во теплоты, поглощённой телом при изменении его состояния, зависит не только от начального и конечного состояний (в частности, от их темп-ры), но и от способа, к-рым был осуществлён процесс перехода между ними. Соответственно от способа нагревания тела зависит и его Т. Обычно различают Т. при пост. объёме (cv) и Т. при пост. давлении (ср), если в процессе нагревания поддерживаются постоянными соответственно его объём или давление. При нагревании при пост. давлении часть теплоты идёт на производство работы расширения тела, а часть — на увеличение его внутренней энергии, тогда как при нагревании при пост. объёме вся теплота расходуется на увеличение внутр. энергии; в связи с этим cp всегда больше, чем cv. Для газов (разреженных настолько, что их можно считать идеальными) разность мольных Т. ср-cv=R, где R — универс. газовая постоянная, равная 8,314 Д ж/(моль•К), или 1,986 кал/(моль•К). У жидкостей и тв. тел разница между ср и cv сравнительно мала.

Из 1-го и 2-го начал термодинамики следует, что ср= Т(дS/дТ)р, а cv=T(дS/дT)v, т. е. Т. пропорц. производной от энтропии S системы по темп-ре Т при соответствующих условиях.

Теор. вычисление Т., в частности её зависимости от темп-ры тела, не может быть осуществлено при помощи чисто термодинамич. методов и требует применения методов статистической физики (знания микроструктуры в-ва). Для газов вычисление Т. сводится к вычислению ср. энергии теплового движения отд. молекул. Это движение складывается из поступат. и вращат. движений молекулы как целого и из колебаний атомов внутри молекулы. Согласно классич. статистике, на каждую степень свободы поступат. и вращат. движений приходится в мольной Т. (сv) газа величина, равная R/2, а на каждую колебат. степень свободы — R; это правило наз. равнораспределения законом. Ч-ца одноатомного газа обладает всего тремя поступат. степенями свободы, соответственно его Т. сv должна составлять 3R/2 (т. <е. <ок. 12,5 Дж/(моль•К), или 3 кал/(моль•град)), что хорошо согласуется с опытом. Молекула двухатомного газа обладает тремя поступательными, двумя вращат. и одной колебат. степенями свободы, и закон равнораспределения приводит к значению сv=7R/2; опыт показывает, что Т. моля двухатомного газа (при обычных темп-рах) составляет 5R/2. Ото расхождение теории и эксперимента связано с тем, что при вычислении Т. необходимо учитывать квантовые эффекты, т. е. пользоваться квантовой статистикой. Согласно квантовой механике, всякая система ч-ц, совершающих колебания или вращения (в т. ч. молекула газа), может обладать лишь определёнными дискретными значениями энергии. Если энергия теплового движения в системе недостаточна для возбуждения колебаний определённой частоты, то эти колебания не вносят своего вклада в Т. системы (соответствующая степень свободы оказывается «замороженной» — к ней неприменим закон равнораспределения). Темп-ра Т, при достижении к-рой закон равнораспределения оказывается применимым к вращат. или колебат. степени свободы, определяется квантовомеханич. соотношением Т ->hn/k, где n — частота колебаний.

Интервалы между вращат. уровнями энергии двухатомной молекулы (делённые на k) составляют всего неск. К и лишь для такой лёгкой молекулы, как молекула водорода, достигают сотни К. Поэтому при обычных темп-рах вращат. часть Т. двухатомных (а также многоатомных) газов подчиняется закону равнораспределения. Интервалы же между колебат. уровнями энергии достигают неск. тысяч К, и поэтому при обычных темп-рах закон равнораспределения неприменим к колебат. части Т. Вычисление Т. по квантовой статистике приводит к результату, что колебат. Т. быстро убывает при понижении темп-ры, стремясь к нулю. Этим объясняется то обстоятельство, что уже при обычных темп-рах колебат. часть Т. практически отсутствует и Т. моля двухатомного газа равна 5R/2 вместо 7R/2.

При достаточно низких темп-рах Т. вообще должна вычисляться с помощью квантовой статистики. Как оказывается, Т. убывает с понижением темп-ры к нулю при Т ®0 в согласии с т. н. принципом Нернста (третьим началом термодинамики).

В тв. (кристаллич.) телах тепловое движение атомов представляет собой малые колебания вблизи определённых положений равновесия (узлов крист. решётки). Каждый атом обладает, т. о., тремя колебат. степенями свободы, и, согласно закону равнораспределения, мольная Т. тв. тела (Т. крист. решётки) должна быть равной 3nR, где n — число атомов в молекуле. В действительности, однако, это значение — лишь предел, к к-рому стремится Т. тв. тела при высоких темп-рах. Он достигается уже при обычных темп-рах у мн. элементов, в т. ч. металлов (n=1, т. н. Дюлонга и Пти закон) к у нек-рых простых соединений (NaCl, MnS(n=2), PbCl2(n=3) и др.); у сложных соединений этот предел фактически не достигается, т. к. раньше наступает плавление в-ва или его разложение.

ТЕПЛОЁМКОСТЬ ср НЕК-РЫХ ГАЗОВ (в Дж/(моль•К), ЖИДКОСТЕЙ И ТВЁРДЫХ ТЕЛ (в кДж/(кг•К) ПРИ ATM. ДАВЛЕНИИ И ПРИ t=25°С

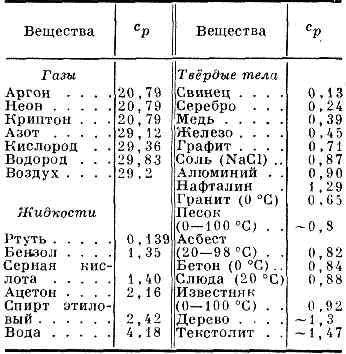
При низких темп-рах решёточная составляющая Т. тв. тела оказывается пропорц. кубу абс. темп-ры (Дебая закон теплоёмкости). Критерием, позволяющим различать высокие и низкие темп-ры, явл. сравнение их с характерным для каждого данного в-ва параметром — т. <н. характеристической, или дебаевской, темп-рой qД. Эта величина определяется спектром колебания атомов в теле и тем самым существенно зависит от его крист. структуры (см. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ). Обычно 6д — величина порядка неск. сот К, но может достигать (напр., у алмаза) и тысяч К (см. ДЕБАЯ ТЕМПЕРАТУРА).

У металлов определённый вклад в Т. дают также и эл-ны проводимости (т. н. электронная Т.). Эта часть Т. может быть вычислена с помощью квантовой статистики Ферми, к-рой подчиняются эл-ны. Электронная Т. металла пропорц. первой степени абс. темп-ры. Она представляет собой, однако, сравнительно малую величину, её вклад в Т. металла становится существенным лишь при темп-рах, близких к абс. нулю (порядка неск. К), когда решёточная Т. (= Т3) становится пренебрежимо малой. У крист. тел с упорядоченным расположением спиновых магн. моментов атомов (ферро- и антиферромагнетиков) существует дополнит. магн. составляющая Т. При темп-ре фазового перехода в парамагн. состояние (в Кюри точке, или, соответственно, Нееля точке) эта составляющая Т. испытывает резкий подъём -наблюдается «пик» Т., что явл. характерной особенностью фазовых переходов II рода.

ТЕПЛОЁМКОСТЬ

кол-во теплоты; поглощаемой телом при нагревании на 1 градус (1 °С или 1 К); точнее - отношение кол-ва теплоты, поглощаемой телом при бесконечно малом изменении его темп-ры, к этому изменению. Т. единицы массы вещества наз. удельной Т., 1 моля вещества-молярной (мольной) Т. Единицами Т. служат Дж/(кг · К), ДжДмоль · К), Дж/(м ³ · К) и внесистемная единица кал/(моль·К).

Кол-во теплоты, поглощённой телом при изменении его состояния, зависит не только от начального и конечного состояний (в частности, от их темп-ры), но и от способа, к-рым был осуществлён процесс перехода между ними. Соответственно от способа нагревания тела зависит и его Т. Обычно различают Т. при пост. объёме (C_V )и Т. при пост. давлении ( С _P), если в процессе нагревания поддерживаются постоянными соответственно объём тела или давление. При нагревании при пост. давлении часть теплоты идёт на производство работы расширения тела, а часть - на увеличение его внутренней энергии, тогда как при нагревании при пост. объёме вся теплота расходуется на увеличение внутр. энергии; в связи с этим С _Р всегда больше, чем C_V. Для газов (разреженных настолько, что их можно считать идеальными) разность мольных Т. С _P - C_V = R, где R- универсальная газовая постоянная, равная 8,314 Дж/(Дмоль·К) или 1,986 калДмоль·К). У жидкостей и твёрдых тел разница между С _Р и C_V сравнительно мала. Т. С _Р нек-рых веществ и материалов приведены в табл. 1 и 2.

Из 1-го и 2-го начал термодинамики следует, что   т. е. Т. пропорц. производной отэнтропии S системы по темп-ре Т при соответствующих условиях.

Теплопроводность