8.Математический маятник. Постановка и решение задачи о движении математического маятника.
Математический
маятник-
это идеализированная система, состоящая
из материальной точки массой
,
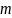подвешенной на растяжимой невесомой
нити , колеблющаяся под действием силы
тяжести.
Математический маятник можно представить как частный случай физического маятника.
-
дуга
-
смещение
Дифф.
Уравнение математического маятника:
или
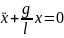
Решение:
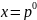
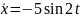
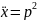
9.Энергия системы , совершающей гармонические колебательные движения.
Кинетическая
энергия-
материальной точки, совершающей
прямолинейные гармонические колебания,
равна:
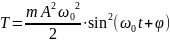
Потенциальная
энергия- материальной
точки, совершающей гармонические
колебания под действием упругой силы
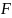равна:
Полная
энергия
находится с помощью суммирования П
и
.
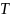полная
энергия прямо
пропорциональна
амплитуде колебаний .
10.Физический маятник. Подстановка и решение задач о движении физического маятника.
Физический
маятник- это
твердое тело, совершающее под действием
силы тяжести колебания вокруг неподвижной
горизонтальной оси , проходящей через
точку о , не совпадающую с центром масс
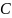тела:
Вращающий момент М :
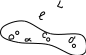приблизительно
равно
- расстояние между ней и центром масс маятника
-
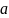угловое смещение
частота:
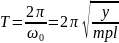
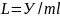– формула
ФМ
– длина от точки О до точки О между ними С
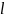– длина
от точки О до точки
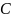
11.Пружинный маятник. Подстановка и решение задач о движении пружинного маятника.
Пружинный
маятник- это
груз массой
, подвешенный на абсолютно упругой силы
:
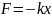где
-жесткость
пружины.
Уравнение
движения маятника в отсутствие сил
трения :
,
Частота
пружинного маятника совершающий
гармонические колебания по закону:
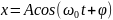
Где
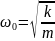период
маятника :
Потенциальная
энергия пружинного маятника:
12.Решение уравнения затухающих колебаний пружинного маятника.
Для
пружинного маятника массой
, совершающего малые колебания под
действием упругой силы :
сила трения пропорциональна скорости
:
-
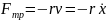коэффициент сопротивления
При
данных условиях закон движения маятника
будет иметь вид:
Используя
формулу :
и принимая , что коэффициент затухания:
Получим
дифференциальное уравнение затухающих
колебаний маятника:
13.Решения уравнения затухающих колебаний физического маятника.
14.Логарифмический декремент колебаний и добротность системы.
и
-амплитуды двух последовательных
колебаний , соответствующих моментам
времени , отличающимися на период , то
отношение:
–декремент
затухания а
его логарифм:
– называется
логарифмическим
декрементом затухания , где
–
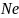число
колебаний, совершаемых за время уменьшения
амплитуды в
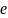раз.
Логарифмический декремент затухания- постоянная величина для данной колебательной системы.
Для
характеристики колебательной системы
пользуются понятием добротность
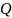которая при малых значениях логарифмического
декремента:
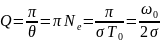
Из
формулы следует , что добротность
пропорциональна числу колебаний
совершаемых системой за время релаксации.
Добротность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.