8. Декомпозиція у моделюванні та системному аналізі.

У наукових дослідженнях велику роль відіграють методи аналізу і синтезу. Ще у XVII ст. Р. Декарт сформулював суть аналітичного методу як розбиття задачі на стільки частин, скільки потрібно для того, щоб її легко розв'язати. Успішність та значення аналізу полягають не тільки в тому, що ціле розбивають на прості частини, а в тому, що, об'єднуючи і синтезуючи ці частини, можна знову утворити ціле.Аналіз і синтез доповнюють, однак не замінюють одне одного. Системні дослідження сполучають обидва вказані методи. Операції розкладання цілого на частини та об'єднання їх у ціле, тобто операції аналізу і синтезу в системних дослідженнях називають декомпозицією та агрегуванням. При застосуванні декомпозиції задачу поділяють на підзадачі, систему - на підсистеми, цілі - на підцілі тощо. Повторюючи цей процес, можна створити ієрархічну деревоподібну структуру поділу. Звичайно, через складність об'єкта, слабку структурованість операцію декомпозиції виконує кваліфікований експерт. Різні експерти можуть давати різні переліки - дерева декомпозиції. Це залежить від їхньої компетентності та методики застосовування. Основою декомпозиції є модель системи. Тому повна декомпозиція (тобто те, наскільки повний список частин цілого) залежить від завершеності моделі, її повноти. З метою забезпечення певної повноти та можливості розширення змістовної моделі, рекомендовано здійснювати логічне замикання списку її елементів компонентою "все інше". Ця компонента буде "мовчазною", коли до неї зачислено все неістотне, проте її наявність постійно нагадує експертові, що, можливо, він не врахував чогось важливого. У процедурі декомпозиції важливо передбачити можливість внесення поправок і доповнень до моделі, використовуючи, наприклад, елемент "все інше" або розукрупнення моделі. Послідовність дій при декомпозиції зображено на рис. Якщо декомпозиція спричинює результат (підціль, підфункцію, підзадачу), який не підлягає подальшому розкладові, тобто простий зрозумілий результат, то його називають елементарним. У деяких задачах (математичних, технічних) елементарність можна класифікувати за певною формальною ознакою. Визначення елементарності справа експертів.

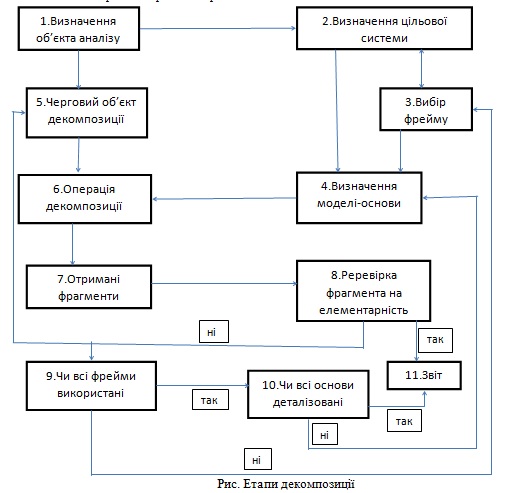
Ускладнення, які виникають під час декомпозиції, трапляються переважно через неінформованість експертів у певних галузях (це потребує додаткових експертів), неповне розуміння системи.

Якщо в науці складність через нерозуміння розцінюється як тимчасове і тому терпиме, то в управлінні діловими, адміністративними, політичними справами нерозуміння часто є неприпустимим.

Іноді недосконалість декомпозиції систем і проектів зумовлена тим, що в її основу покладено тільки позитивні складові, а негативними нехтують. Тому під час розробки проекту експерти повинні виявити усі його можливі негативні наслідки.

9. Декомпозиція односекторної моделі економіки

Декомпозиція (дезагрегування), а також агрегування деякої математичної моделі системи взагалі є справою творчою, яка потребує не меншого мистецтва, ніж сам процес складання базової початкової моделі.

Наведемо дезагрегацію оптимізаційної макроекономічної моделі національної економіки. Вона спричинює оптимізаційну динамічну модель багатогалузевої економіки.

Нехай економіка має довільну кількість n галузей. Кожну галузь описано власним рівнянням відтворення виробничих фондів (капіталів) з припущенням (для спрощення задачі) щодо швидкого використання інвестицій без урахування запізнення на приріст виробничого капіталу та на амортизаційні відрахування, тобто для кожної i-ої галузі:

, (1)

де - інтенсивність валових інвестицій в i-ій галузі; - коефіцієнт амортизаційних відрахувань i-ої галузі; - основний виробничий капітал i-ої галузі.

Як і в одногалузевій економіці, при відомому рівні виробничих капіталів у початковий момент часу t₀

Kⁱ (to)=K_oⁱ, і = (2)

виробничі можливості галузей обмежено виробничими функціями галузей Fⁱ(t, Kⁱ(t), Lⁱ(t)), тобто для інтенсивного виробництва X (t) i-ої галузі справедлива нерівність:

0≤ X^і(t)≤Fⁱ(t, Kⁱ(t), Lⁱ(t)), to ≤ t ≤tj, i = , (3)

де Lⁱ (t) - трудові ресурси i-ої галузі.

Міжгалузеві зв'язки багатогалузевої економіки в динамічному варіанті можна подати подібно до статичної моделі багатогалузевої економіки Леонтьєва за допомогою балансових рівнянь виду:

(4)

Різниця полягає у тому, що технологічні коефіцієнти галузей економіки, які складають її технологічну матрицю, та інтенсивність кінцевих продуктів Yⁱ є функціями часу a_ij(t), Yⁱ =Yⁱ(t).

Крім того, до рівнянь необхідно додати балансові рівняння

(5)

де dij - структурні коефіцієнти основних виробничих фондів;

Cⁱ(t) - інтенсивність невиробничого споживання продукції i- ої галузі.

Трудові ресурси Lⁱ обмежені нерівністю: (6)

де L_max(t) - загальна кількість трудових ресурсів економіки в момент часу t.

З економічних міркувань випливають ще такі обмеження:

Iⁱ(t) ≥ 0, Cⁱ(t) ≥ , Kⁱ(t) ≥ 0, i= , (7)

де - мінімальний рівень невиробничого споживання продукції i-ої галузі, необхідний суспільству.

У моделі вважають відомою інформацію щодо початкових значень виробничих капіталів , коефіцієнтів амортизації галузей , матриці прямих виробничих витрат A=(a_ij(t)), матриці структури фондів сумарних трудових ресурсів , які визначають за демографічним прогнозом та виробничими функціями галузей Fⁱ(t, Kⁱ, Lⁱ).

В оптимізаційній задачі пошуку найкращого розвитку економіки на період часу [t₀,t₁]потрібно визначити багатовимірну функцію V(t):

V(t)=(X(t), Y(t), I(t), C(t), K(t), L(t)), t є[to,tj] яка має шість компонент

X(t)=Xⁱ(t), (i= 1, 2,…, n);

Y(t)=Yⁱ(t), (i= 1, 2, ..., n);...; L(t)=Lⁱ(t), (i= 1, 2,..., n),

та для якої сумарна дисконтована корисність споживання невиробничої продукції економіки J(V) досягає максимуму:

де U(t, C(t))=U(t, C¹(t),...,Cⁿ(t)) - функція, яка визначає корисність вектора інтенсивності невиробничого споживання C(t)=(Cⁱ(t)) (i= 1, 2, ..., n) у момент часу t для суспільства загалом (або функція корисності інтенсивності споживання C);

D(t) - функція дисконтування.

Нагадаємо, що компоненти функції V мають задовольняти умови (1)-(7). Зауважимо, що введення до моделі виробничих функцій дає змогу врахувати можливості взаємного заміщення праці та виробничого капіталу в галузях і залежність продуктивності від фондоозброєності галузей.