60. Графи та їхнє застосування.

Графи використовують у сіткових моделях та методах планування, у теорії алгоритмів, у теорії інформації, соціології, хімії, фізиці, біології, математиці. Останніми роками все більше коло економіко-математичних задач для свого вирішення залучають методи теорії графів. Доброю ілюстрацією цього є вирішення задач оптимізації потоків у мережах.

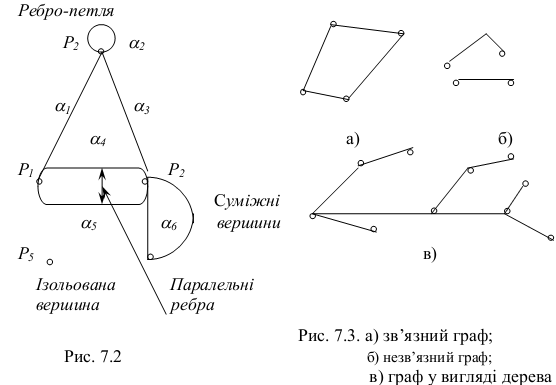
Граф G = G(V, E) – це сукупність множини V вершин точок) і множини ребер E (зв’язків), що з’єднують деякі (або ж усі) вершини. Пари вершин бувають з’єднаними кількома ребрами. Практичне значення переважно мають скінченні графи, в яких кількість вершин є скінченною величиною.

Граф називають орієнтованим, якщо на кожному ребрі стрілкою задано напрям, тобто виокремлено початкову і кінцеву вершини ребра, у протилежному випадку граф називають неорієнтованим. Шляхом у графі називають таку послідовність ребер від деякої початкової вершини p₁ до кінцевої вершини p_n, в якій кожні два сусідніх ребра мають загальну вершину та жодне ребро не трапляється понад один раз. Цикл – це шлях, де початкова та кінцева вершини збігаються. Граф називають зв'язним, коли в ньому існує шлях, який з’єднує будь-яку пару вершин (рис.7.3,а). У протилежному випадку граф називають незв’язним (рис.7.3,б). Зв’язний граф, що не містить циклів, називають деревом (рис.7.3, в).

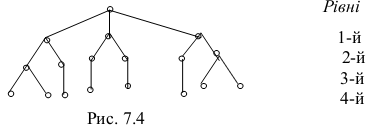
Графи-дерева використовують з метою опису потенційних ігор у теорії ігор, розв’язування важливих прикладних оптимізаційних задач цілочислового програмування, а також для опису ієрархічних структур і систем. Ієрархія означає розширювання частин чи елементів цілого за певним порядком від вищого рівня до нижчого. На рис. 7.4 зображено граф, який відповідає ієрархічній структурі. У ньому виокремлюють кілька рівнів, причому найвищому першому рівню відповідає одна вершина. Таке дерево називають деревом з ієрархічною формою.