54.Застосування дискретного програмування у системному аналізі

Дискретне програмування є розділом математичного програмування, що вивчає задачі, в яких на значення частини чи всіх змінних величин накладено вимогу дискретності.

У термінах дискретного програмування формулюють різноманітні економічні задачі: планування і управління, проектування та розміщення; задачі розміщення, комівояжера

та про призначення; задачі теорії розкладів, чимало інших економічних , військових задач.

Найкраще вивчено задачі лінійного дискретного програмування. Це звичайні задачі лінійного програмування, лише шукані змінні повинні мати дискретне значення. Ці типи моделей відображають задачі з неподільностями. У них змінні величини є фізично неподільними.

Задачі з неоднорідною розривною цільовою функцією:

∑ⁿ_j=1C_j(x_j)→min

∑ⁿ_j=1a_ijx_j≥A_i, i=1,2,…m

x_j≥0 j=1,2,…,n

C_j(x_j)=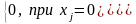

Такі задачі ще називають задачами з постійною складовою.

Серед цих задач найкраще вивчено задачі транспортного типу з фіксованими доплатами. Їхня цільова функція має вигляд:

∑^m_i=1∑ⁿ_j=1 (C_ijx_ij+d_ijy_ij),

де y_ij=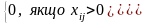

Доброю ілюстрацією економічної задачі, відображеною моделлю дискретного програмування, є варіантна задача розміщення виробництва з такою постановкою:

В m (i=1, 2, …, m) можливих точках розміщення виробництва потрібно розмістити виробництво продукції. Щодо кожної з цих точок існує набір можливих варіантів проектів підприємств. До цих варіантів належать не тільки проекти нових підприємств, але

й варіанти реконструкції діючих підприємств, їхня ліквідація тощо. Загальна їхня кількість дорівнює H (h=1, 2, …, H). Відомо n (j=1, 2, …, n) споживачів продукції, потреба кожного з них становить Bj. Вартість реалізації проекту (враховуючи термін окупності) разом із затратами на випуск продукції дорівнює Aih.

Математична модель цієї задачі має вигляд:

∑^m_i=1∑^H_h=1A_ihx_ih+∑^m_i=1∑ⁿ_j=1t_ijy_ij→min

∑ⁿ_j=1y_ij=∑^H_h=1A_ihx_ih, i=1,2,..m

∑ⁿ_j=1y_ij=B_j, j=1,2,..n

∑^H_h=1x_ih=1, i=1,2,..m

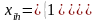
де xih – цілочислова змінна, яка вказує на прийняття h-го проекту в і-ій точці можливого розміщення виробництва; yij – транспортні зв’язки і-го підприємства (виробника продукції) і j-го споживача цієї продукції; tij – затрати на перевезення одиниці продукції від і-го виробника до j-го споживача. Умови (7.52) і (7.53) забезпечують прийняття в кожній точці розміщення виробництва лише одного з можливих проектів підприємств.

Найпоширенішими методами розв’язування таких задач є:метод відсікання, комбінаторні методи, наближені методи.

Виникнення дискретного програмування пов’язують з опублікуванням американськими вченими Фулкерсоном-Джонсоном і Данцігом ідеї методу відсікання, проте розвиток методів розв’язування задач дискретного програмування почався після створення Гоморі першого алгоритму відсікання.

55.Застосування динамічного програмування у системному аналізі

Динамічне програмування - розділ математичного програмування, який розглядає багатокрокові методи пошуку розв’язків. Розв’язування задачі математичного програмування з допомогою методів динамічного програмування здійснюється поетапно, тобто динамічно і послідовно.

Основним методом динамічного програмування є метод рекурентних співвідношень, створений американським вченим Р. Белманом у 50-х роках ХХ ст., в основі якого закладено принцип оптимальності: якщо керування процесом оптимальне, то воно оптимальне для процесу, який залишився після здійснення першого кроку. Передісторію процесу і параметри керування на попередніх кроках не беруть до уваги.

Математичне формулювання принципу оптимальності Белмана виражено рівняннями, розв’язок яких визначає оптимальну поведінку в керуванні процесом. Для числового відшукання оптимальних параметрів керування ефективним є метод послідовного аналізу варіантів, розроблений на початку 60-х років ХХ ст. в Інституті кібернетики НАН України

українськими вченими В.С. Міхалевичем і Н.З. Шором, суть якого полягає у послідовному конструюванні конкурентоспроможних варіантів.