52. Застосування лінійного та нелінійного програмування у системному аналізі

1)Одним з головних розділів математичного програмування є лінійне програмування. Це область математики, що вивчає задачі відшукання екстремуму (максимум, мінімум) лінійної функції на області допустимих значень змінних, окресленої обмеженнями у вигляді лінійних рівнянь та нерівностей, які пов’язують ці змінні.

До задач лінійного програмування зводиться широке коло задач управління функціонуванням економічних систем.

Термін лінійне програмування започаткували 1951 р. американські учені Дж. Данціг і Т. Купманс стосовно шуканих змінних, які в економічному розумінні інтерпретують як програму чи план функціонування економічного об’єкта.

Загальну задачу лінійного програмування сформульовано так: потрібно знайти змінні x₁, x₂, …, x_j, …, x_n, які надають екстремального (мінімального, максимального ) значення цільовій функції: 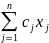(7.1) і задовольняють обмеження : 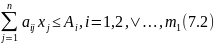; ; 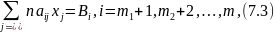xj>=0 , j=1, 2, …, n, (7.4) де c_j (j=1, 2, …, n); a_ij (i=1, 2, …, m; j=1, 2, …, n); A_i, B_i (i=1, 2, …,m) – заздалегідь відомі величини. Лінійне програмування є найбільш вивченим розділом математичного програмування .

Задачами лінійного програмування є транспортна задача, теорії ігор, положення теорії двоїстості та інші.

Лінійне програмування знаходить своє застосування у різних сучасних і класичних областях математики: теорії графів, комбінаториці, теорії наближення функцій, теорії лінійних нерівностей та інших.

2)Важливим розділом математичного програмування є нелінійне програмування. Цей розділ математичного програмування вивчає методи відшукання розв’язків багатовимірних екстремальних задач з обмеженнями, причому функціональні залежності у цих задачах не вважають лінійними. Суть загальної задачі нелінійного програмування полягає у визначенні n-вимірного вектора x=(x₁, x₂, …, x_n) з заданими функціями f(x), g1(x), g2(x), …, gm(x), який надавав би функції f(x) глобального екстремуму і задовольняв би умови: g_i(x) 0, i=1, 2, …, m; x_j 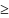0, j=1, 2, …, n, які означають множину M допустимих значень вектора X.

Нелінійне програмування охоплює дуже широке коло задач математичного програмування. Важливим для пошуку розв’язання задачі нелінійного програмування є метод множників Лагранжа, який передбачає побудову функції Лагранжа: F(x,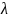 )=f(x)+ 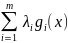де число 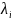– множники Лагранжа.

З метою визначення вектора x* , який належить множині M і надає мінімального значення функції f(x), потрібно знайти m чисел 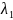, , 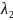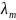і n чисел x₁, x₂, …, x_n вектора x* ,які задовольняють систему m+n рівнянь:

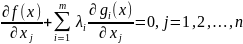
g_I(x)=0, i=1 ,2,…, m.

Для розв’язку цієї системи потрібно, щоб хоча б один із визначників m-го порядку матриці

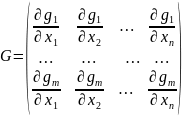не дорівнював нулю.

53.Застосування блокового програмування у системному аналізі

Блокове програмування – розділ лінійного програмування, який вивчає методи зведення розв’язування задач лінійного програмування великого обсягу до розв’язування послідовності задач меншої розмірності. Основу блокового програмування становить метод декомпозиції. Американські математики Дж. Данциг і Ф. Вулф 1960 р. вперше спробували формалізувати розв’язок математичних моделей великої розмірності, розробивши так званий принцип розкладу для задач лінійного програмування. На цьому принципі базується запропонований ними метод блокового програмування. Суть цього методу зводиться до наступного. Розглядаючи структуру деяких реальних економічних задач, можна зауважити, що вони складаються з декількох часткових задач, пов’язаних певними загальними обмеженнями. Прикладом такого випадку є ситуація розвитку виробництва декількох галузей на одній території. Ці галузі можуть не залежати одна від одної, і їхній розвиток лімітований різними умовами, проте територія у них одна, а це означає, що трудові, енергетичні, природні ресурси, транспортна мережа у них спільні. Спільні у них і екологічні проблеми. Аналогічні ситуації можуть траплятися і з однією галуззю, коли виробництво її продукції мало пов’язано між собою, однак існує певне число спільних обмежень, які накладаються на розвиток галузі загалом. У такому випадку матриця умов задачі оптимального розвитку регіону чи галузі набуває спеціальної, так званої блоково-діагональної структури у вигляді:

Де Ω - – число видів продукції, виробництво яких слабо пов’язане між собою; A^(w) = ||a_ij^(w)|| - матриця коефіцієнтів затрат-випуску продукції групи w розмірності n_xm_w n - число обмежень у виробництві продукції групи w , які впливають і на інші групи продукції, виробництво яких ми оптимізуємо у регіоні загалом. Таку структуру матриці коефіцієнтів затрат-випуску задачі оптимізації розвитку виробництва продукції даного регіону у загальному вигляді можна записати так: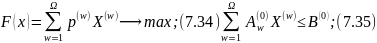

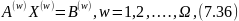
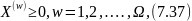
Де Х = (Х⁽¹⁾_, Х⁽²⁾ , …, Х^(w)_,…., X^(Ω)) – розв’язок задачі (7.34) - (7.37);

B^(w) _- обмеження, властиві тільки групі продуктів w , представлених вектором - стовпчиком розмірності n_w; B^(w) B⁽⁰⁾ – обмеження спільні для всіх видів продукції, предствалених вектором, стовпчиком розмірності n. Основне положення, на якому ґрунтується метод блокового програмування, полягає у наступному: виходячи з того, що обмеження кожного блоку утворюють випуклі множини, будь-який розв’язок окремого блоку можна представити у вигляді лінійної комбінації його базисних розв’язків:

X^(w) = 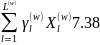. Виходячи з цього, задача (7.34)-(7.37) розпадається на координуючу задачу:

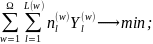7.39

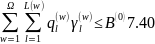
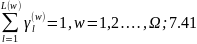
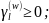l=1,2,…..L^(w); w = 1,2,….Ω; 7.42

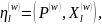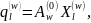Де 7.43 7.44

І підзадачі:

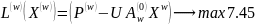
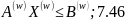X^(w) ≥0, 7.47

Де U = (U₁, U₂ , …., U_j,…….,U_n) - вектор двоїстих оцінок умов (7.40).

Реалізуючи метод блокового програмування, спочатку розв’язують координуючу задачу (7.39)-(7.42), визначають двоїсті оцінки, які відповідають спільним обмеженням (7.40). З їхньою допомогою будують цільові функції окремо для кожної з підзадач. Оптимальні значення цих цільових функцій, отриманих у результаті розв’язування підзадач, використовують з метою перевірки базисного розв’язку координуючої задачі на оптимальність та вибору вектора, який потрібно ввести у базис, для якої даний базисний розв’язок виявиться неоптимальним. З метою перевірки базисного розв’язку координуючої задачі на оптимальність використовують умову:

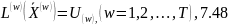
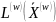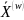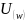- значення цільової функції для оптимального плану підзадачі w, а - оцінка обмеження w у (7.42). Якщо умова (7.48) не виконується, в базис координуючої задачі необхідно ввести вектор з найменшою відносною оцінкою, яку визначають з формули: