51. Застосування математичного програмування у системному аналізі

Математичне програмування - розділ прикладної математики, що вивчає багатовимірні екстремальні задачі з обмеженнями. Назва математичного програмування походить від лінійного програмування, яке є його складовою частиною.

Засвоєння математичного програмування полягає у визначенні вектора Х=(х1,х2,...хm) з певної області М, утвореної умовами fj(x)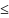 0, j=1, 2, …, m, який надає функції f(x) екстремального (мінімального чи максимального) значення. Функцію f(x) називають цільовою, а множину М множиною допустимих значень векторів. Сформульована задача принципово відрізняється від класичної задачі визначення умовного екстремуму, бо в ній є обмеження у вигляді нерівностей (що робить необхідним визначення екстремуму на границі області М) і тому скористатися класичними методами аналізу функцій практично неможливо. З метою дослідження таких задач розроблено самостійні теорії.Розвиток теорії математичного програмування здійснено шляхом використання особливостей функцій цільових і функцій умов. Серед задач лінійного програмування особливо важливе місце займають задачі транспортного типу, для розв’язання яких, завдяки специфічній структурі обмежень, створено ефективні спеціальні методи – метод потенціалів, розподільчий метод, угорський метод та ін.

Успіхи у розвиткові теорії лінійного програмування сприяли розвиткові інших розділів математичного програмування, які спочатку розвивалися окремо зі своїми особливими задачами та методами. Подальший розвиток цих розділів все більше заповнював прогалини між ними і математичне програмування ставало цілою теорією екстремальних задач. Сьогодні можна виокремити низку основних груп задач і методів їхнього розв’язування.

Опуклі задачі. До цього типу належать задачі, у яких цільова функція і функції умов (задачі математичного програмування) є опуклими. Зокрема, сюди зачислено задачі лінійного програмування та квадратичного програмування, у задач якого цільова функція – квадратична, а функції умов – лінійні. Задачі опуклого програмування мають таку особливість: якщо невеликі зміни допустимого розв’язку не зумовлюють допустимого розв’язку з меншим значенням цільової функції (задача на мінімум), тобто цей допустимий розв’язок є локальним оптимумом, то він же є і глобальним оптимумом. Числові методи розв’язування цього типу задач є ітеративними, їх класифікують у три групи:

1. Методи глобальних переміщень. На першому етапі обирають напрям, за яким здійснюється переміщення, на другому – обирають серед них найкращий допустимий (метод послідовного покращення розв’язку для задач лінійного програмування, метод можливих напрямів для задач опуклого програмування). 2. Методи локальних переміщень. Вони відзначаються тим, що переміщення здійснюється з досить малим фіксованим кроком. 3. Методи послідовного переміщення. Ці методи дають змогу здійснити переміщення в область допустимих розв’язків з-за меж цієї області. Типовим методом є метод проекції градієнта. Методи лінійного і опуклого програмування є основою щодо різноманітних методів розв’язування інших задач математичного програмування.

Неопуклі задачі. При допомозі методів локальних переміщень можна знайти локальний оптимум таких задач. Однак уся складність полягає у тому, щоб серед локальних оптимумів знайти глобальний.

Динамічні задачі. Характерною особливістю цих задач є те, що у їхній постановці і у методах їхнього розв’язування використовують динамічне, тобто поступове і послідовне прийняття рішень. Головним з методів динамічного програмування є метод рекурентних співвідношень Р. Белмана, в основу якого закладено принцип оптимальності: якими б не були первісний стан процесу і управлінські рішення до певного моменту часу, наступні управлінські рішення повинні бути оптимальні для цього процесу у наступні моменти часу. Дискретні задачі. Особливість цих задач – додаткова умова дискретності, зокрема і цілочисловості, накладена на змінні. З метою вирішення цих задач використовують дві групи методів. Перша - для вирішення задач лінійного програмування з додатковими умовами цілочисловості на шукані змінні. При допомозі цих методів спочатку розв’язують задачу, отриману з початкової зняттям умови цілочисловості. А потім, якщо отриманий розв’язок не задовольняє вимоги цілочисловості – скорочують множину допустимих розв’язків. До таких методів належить метод Р. Гоморі і його модифікації. Друга група методів базована на скороченні перегляду варіантів розв’язків. Ці методи називають методами гілок і границь. Вчені Київського інституту кібернетики В.С. Міхалевич і Н.З. Шор розробили ефективний метод послідовного аналізу варіантів, який дає змогу скоротити множину допустимих розв’язків задачі. Стохастичні задачі. Розділ математичного програмування, який вивчає методи розв’язування задач прийняття рішень в умовах ризику і невизначеності і ці задачі використовують випадкові величини, що підлягають певному закону розподілу, називають стохастичним програмуванням. Методи математичного програмування використовують також у вирішенні проблем теорії ігор.