36. Модель національної економіки

Модель національної економіки – тип економіко-математичної моделі, завдяки якій аналізують розміщення виробничих ресурсів і розподіл виробленого національного продукту серед усіх громадян країни. Розміщення ресурсів і розподіл виробленої продукції є головною функцією національної економіки незалежно від того, чи є вона централізованою, чи децентралізованою. Однак у децентралізованій економіці таке розміщення і розподіл відбувається шляхом індивідуальних, конкурентних, конфліктних дій. Проілюструємо це на прикладі моделі конкурентної економіки вальрасівського типу – типічної децентралізованої економічної системи. Формально ця система відзначається такими властивостями: вона налічує скінченне число виробників і споживачів, які діють відповідно до своїх власних інтересів. Усі чинники виробництва – праця і капітал – перебувають у приватній власності споживачів і залучаються у виробництво керівниками виробництва. Вироблену продукцію розподіляють між споживачами. Зауважимо, що це є можливим за умови розв’язання конфлікту між індивідуальними інтересами різних учасників процесу виробництва і споживання. У нашому випадку передбачено усунення конфлікту не вольовими методами, а через конкурентний ринковий механізм, який ґрунтується на регулюючій дії системи цін. Учасники ринку впливати на ціну не мають змоги. Вважається, що існує система цін, за якої розподіл ресурсів і продукції здійснюється вирішенням конфлікту між індивідуальними інтересами. Таку погоджувальну ситуацію називають конкурентною рівновагою. Питання щодо доцільності і живучості децентралізованої економічної системи зводиться до питання існування конкурентної рівноваги. До базової дезагрегованої моделі національної економіки зачислено m споживачів (i=1, 2, ..., m), K виробників (k=1, 2, ..., K) та n категорій продукції (j= 1, 2, ..., n). Кожний споживач має поле переваг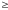 (xi ) і xi 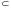Rn , де Хі – множина усіх можливих наборів (x1,x2,...,xп ) споживчих благ (продукції), доступних і-му споживачеві; xj – кількість j -го споживчого блага, доступного і-му споживачеві; Rn – множина наборів споживчих благ, на якій визначено переваги і-го споживача. 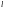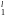Крім цього, і-ий споживач володіє початковою стартовою власністю, визначеною вектором: Q = (Q ,Q ,...,Q ) Rn, j -та компонента якого Q означає кількість j -ої продукції у цій стартовій власності . Кожному виробникові доступна виробничо-технологічна множина y_k . Розподіл виробництва здійснюється (супроводжується) вибором процесу y_e^k з технологічної множини y_k для кожного k=1, 2, …, K. Тоді 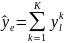виражає l-ий сукупний процес. Ці сукупні процеси становлять сукупну технологічну множину y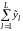 утворену як векторна сума множин 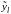, що стає технологічною множиною для національної економіки загалом. Сукупна початкова, стартова власність Q=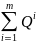 і сукупна технологічна множина Y відбивають сукупну пропозицію {Q}+Y. Початкова власність – це споживчі товари, напівфабрикати, стаціонарне капітальне обладнання, земля, природні ресурси, робоча сила. Розподіл споживання здійснюється шляхом вибору меню споживання (набору споживчих благ) xi Х для кожного і=1, 2, …, m. Сукупним попитом буде: 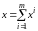. Набір з k+m+1 векторів (x 1 ,x 2 ,...,x m ,y 1 ,y 2 ,...,y k ,p ), який складається зі споживчих меню xi Xi , (i=1, 2,…,m), виробничих процесів yk Yk (k=1, 2, …,K) та n-мірного вектора цін 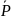, називають конкурентною рівновагою в моделі національної економіки, якщо досягнуто виконання таких умов: 1) максимальний прибуток кожного виробника за заданими цінами:

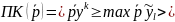для всіх 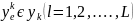(k 1,2,...,K ) ;

2) оптимальний набір споживчих благ серед можливих , які відповідають бюджетному обмеженню:

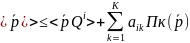
3) збалансованість сукупного попиту і пропозиції:

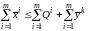
Вектор 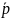називають вектором цін рівноваги. Споживачі і виробники намагаються досягти найкращого свого стану, вважаючи ціни заданими. Умова 1 означає, що кожний виробник досягає свого найбільшого прибутку цілковито за рахунок вибору вектора затрат-випуску з можливих для нього, причому ціни є некерованими.

Виробники сплачують споживачам-акціонерам дивіденди в сумі 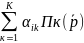. Умова 2 означає, що споживач надає перевагу наборові споживчих благ, узгоджуючи його зі своїм бюджетом і заданими цінами.

За умови позитивних цін на товар (умова 3) попит і пропозиція на нього зрівноважуються . Під час розподілу виробництва і споживання вибір набору споживчих благ зовсім не обов’язково повинен відбуватись з ініціативи індивідуальних споживачів і виробників. Наприклад, за умови цілковито центр алізованої економіки планові органи спонукатимуть до вибору споживчого меню і планів виробництва, які суперечать власним інтересам споживачів і виробників, і внаслідок чого відбуватиметься конфлікт з їхніми міркуваннями щодо власної вигоди. У граничному випадку - економіка з досконалою конкуренцією - ринковий механізм спонукатиме здійснювати розподіл виробництва і споживання відповідно до індивідуальних ініціатив, формуючи систему цін рівноваги.

Моделі економічної динаміки – частковий випадок макроекономічних моделей довготермінового розвитку, формально вони представлені тим чи іншим видом функціонального рівняння. Найвідомішою моделлю економічної динаміки є модель зростаючої економіки, запропонована американським вченим Дж. фон Нейманом.

Основний зміст задачі, описаної моделлю Неймана, полягає у визначенні максимального технологічного темпу зростання 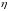, який економічна система може витримати як завгодно довго: 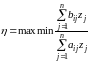де a_ij і b_ij – елементи матриць А і В, відповідно, затрат і випуску розмірності (mхn), які вказують на затрати чи випуск і-ої продукції за умови одиничної інтенсивності j -го технологічного способу; z_j – інтенсивність j -го технологічного способу.

Якщо припустити, що х(t) – n-вимірний вектор затрат у момент t, y(t+ 1) – n-вимірний вектор випуску продукції у момент (t+1) ; z_t - технологічна множина, утворена всеможливими парами (x,y), то технологічно можливу траєкторію можна записати як послідовність {(x,y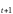 ) z , t=0, 1, 2,…, T-1}. Технологічному темпові зростання відповідає траєкторія {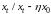 } t=1, 2,…, T, яку називають траєкторією максимально збалансованого зростання, або нейманівською траєкторією. Її ще називають магістраллю, або нейманівським променем. Для замкненої економіки модель Неймана матиме вигляд: →max; BZ AZ.

Максимальне число , за якого виконується умова 3, є технологічним темпом зростання 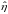. Вектор 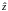, за якого досягнуто , називають оптимальним, він є магістраллю або нейманівським променем.