35. Математичний опис динамічних систем

Якщо розглядати вихід динамічної системи y(t) , наприклад, вектор деякого лінійного простору як реакцію на її входи x(t), то можна записати y(t) як перетворення Ф процесу x(t): y(t) = Ф(x(t)) .

У моделі чорної скриньки Ф є невідомим. У моделі білої скриньки, коли є повна інформація щодо структури системи, Ф відоме. Якщо ми маємо справу з сірою скринькою (тобто інформація щодо структури системи є неповною), виникають різні варіанти щодо Ф . У параметричній моделі перетворення Ф відоме з точністю до деякої сукупності 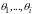. У непараметричній моделі можна вказати тільки деякий клас перетворень П, до якого належить

конкретне перетворення Ф зазначеної системи.

Важливою внутрішньою характеристикою динамічної системи є її стан z(t), значення якого у момент часу t визначає значення виходу системи y(t) .

Стан z(t) розглядають як носій інформації, необхідної для передбачення впливу сучасного на майбутнє системи.

Множину можливих станів системи Z називають фазовим простором системи. Якщо стан Z є вектором z(t) = z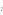 (t), то його компоненти z (t) називають фазовими координатами системи.

До математичної моделі системи зачислено рівняння, які описують залежності виходу системи від її стану, стану системи від входу та закономірності зміни станів системи.

Перша залежність має вигляд: Y(t) = g(z(t),t), t T, (5.1)

де Т – проміжок часу, на якому досліджують систему; g – відображення g: ZхT→Y (g називають відображенням виходу); y – множина значень виходів.

З метою опису другої залежності треба ввести параметричну сім'ю відображень 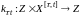(перехідних відображень), для яких: Z(t) = 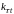(Z( ), X)= q(t, , Z( ), X) (5.2)

Це фактично означає, що висунуто таке припущення: стан у будь-який момент часу t (t> ) однозначно визначається станом Z( ) у момент та відрізком реалізації входу X від до t ( q -відображення входу). Згідно зі співвідношеннями (5.1) і (5.2) модель системи, що відповідає “білій скриньці”, описується множиною входів, станів, виходів, а також зв’язків між ними:

q g

X → Z → Y .

Конкретизуючи множини X, Y, Z, відображення g та q можна отримати різні класи систем та їхніх моделей. Наприклад, система є дискретною або неперервною залежно від того, чи Т є проміжком на множині дійсних R чи у множині натуральних чисел N.

Якщо X, Y, Z – лінійнi простори, а g та q – лінійні оператори, то систему називають лінійною. Якщо простори X, Y, Z – нормовані, і g та q – неперервні, а функція зміни станів z(t) є диференційованою і закон зміни станів (еволюція або рух системи) описано диференційним рівнянням вигляду Z'(t) = f (t, z(t), x(t)), t T, (5.3) то систему називають гладкою.