
- •1. Основні засади системного аналізу
- •2. Поняття системи, її властивості та структура
- •Пов'язані зі структурою
- •Пов'язані з ресурсами та особливостями взаємодії із середовищем
- •3. Взаємодія систем із зовнішнім середовищем
- •4. Класифікація систем
- •5.Особливості, структура та функціонування ек. Систем.
- •6.Особливості, структура та функціонування виробничих(вир.) систем.
- •7.Особливості фінансових систем
- •8. Декомпозиція у моделюванні та системному аналізі.
- •9. Декомпозиція односекторної моделі економіки
- •10. Агрегування в моделях міжгалузевих зв’язків
- •11.Проблема невизначеності та випадковості
- •12.Інформаційні аспекти дослідження систем. Інформація та її передавання
- •13. Поняття управління. Управління і система
- •14. Типи (способи) управління системами
- •15.Прості системи управління
- •16.Системи управління з адаптацією
- •17.Модельні системи управління
- •18.Семіотичні системи управління
- •Етапи управління
- •20.Особливості управління у виробничих системах
- •21. Базова модель прийняття рішень та її структура
- •22. Головні завдання системного аналізу та його основні етапи.
- •Процес виконання системного аналізу
- •23. Формулювання проблеми у системному дослідженні
- •24. Визначення цілей і формування критеріїв у системному дослідженні
- •Генерування альтернатив у системному дослідженні
- •26.Алгоритмізація системних досліджень.
- •27.Проблеми реалізації системних досліджень
- •28.Способи вирішення проблеми та етика системних досліджень
- •29. Поняття моделі та суть методу моделювання.
- •30. Класифікація моделей.
- •31. Головні етапи моделювання економічних процесів
- •32. Моделі типу “життєвий цикл”
- •33. Модель чорної скриньки.
- •34.Статичні і динамічні моделі систем.
- •35. Математичний опис динамічних систем
- •36. Модель національної економіки
- •Статичні матричні макроекономічні моделі
- •Моделі виробничих систем
- •39.Основні характеристики виробничих функцій. Випадок функції Кобба-Дугласа
- •40.Функції виробничих затрат
- •41.Сіткові моделі
- •42.Проблема класифікації методів системного аналізу
- •43.Метод колективної генерації ідей або "мізкової атаки"
- •44.Метод сценаріїв
- •45.Методи експертних оцінок
- •46. Метод Дельфі
- •47. Метод дерева цілей.
- •48. Морфологічні методи (або метод Цвіккі)
- •49. Особливості застосування кількісних методів у системному дослідженні
- •51. Застосування математичного програмування у системному аналізі
- •52. Застосування лінійного та нелінійного програмування у системному аналізі
- •53.Застосування блокового програмування у системному аналізі
- •54.Застосування дискретного програмування у системному аналізі
- •55.Застосування динамічного програмування у системному аналізі
- •56.Статистичні методи у дослідженні систем.
- •57.Теорія масового обслуговування
- •58.Теорія ігор.
- •59.Машинне імітування.
- •60. Графи та їхнє застосування.
21. Базова модель прийняття рішень та її структура
Модель за означенням є наближеним відображенням реальної дійсності, тому очевидним є те, що моделі прийняття рішень охоплюють лише певні, головні параметри, які характеризують основні зв'язки між ними та стан реальної дійсності.n Збільшення кількості параметрів і залежностей між ними зумовлює необхідність спрощення їхньої суті, що, в свою чергу, спричинює зниження рівня системного підходу під час вирішення поставленої проблеми. У випадку математичних моделей можна представити єдиний варіант уникнення протиріччя між рівнем комплексності та змістовності, а саме - обмеження області впливу окремих параметрів і залежностей. Це також сприяє узгодженості усіх моделей на рівні загальнометодологічних і методичних положень теорії прийняття рішень. Представимо узагальнену модель вирішення проблеми, яка може виконувати роль базової, на основі якої можуть розроблятися моделі конкретних проблемних ситуацій. Спочатку опишемо у загальних рисах проблему, зокрема - проблемну ситуацію та її елементи.
Нехай
існує проблемна ситуація V,
щодо якої необхідно прийняти рішення
протягом часу T, і з цією метою виділено
ресурси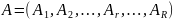 .
Опишемо характеристики, які визначають
зазначену проблемну ситуацію і які
необхідно визначити при постановці
проблеми. Зовнішнє середовище впливає
на ситуацію через некеровані чинники
.
Опишемо характеристики, які визначають
зазначену проблемну ситуацію і які
необхідно визначити при постановці
проблеми. Зовнішнє середовище впливає
на ситуацію через некеровані чинники
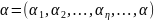 .
Певна
конкретна комбінація їхніх числових
значень визначає одну з п
можливих
станів зовнішнього середовища
.
Певна
конкретна комбінація їхніх числових
значень визначає одну з п
можливих
станів зовнішнього середовища
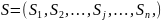 .
Вектор
.
Вектор
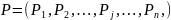 описує
імовірності настання
відповідного
стану. Системи керованих чинників,
комбінація числових значень яких формує
відповідні альтернативи дій, описано
вектором
описує
імовірності настання
відповідного
стану. Системи керованих чинників,
комбінація числових значень яких формує
відповідні альтернативи дій, описано
вектором
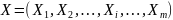 ,
а варіанти дій представлено вектором
,
а варіанти дій представлено вектором
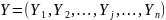 .
Систему цілей також визначено у результаті
постановки задачі - вектором
.
Систему цілей також визначено у результаті
постановки задачі - вектором
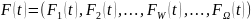 .
Відповідність результатів дій Y
щодо
встановленої мети визначають системою
критеріїв
.
Відповідність результатів дій Y
щодо
встановленої мети визначають системою
критеріїв
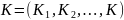 .
Корисність дії
Yj
визначають
функцією корисності.
.
Корисність дії
Yj
визначають
функцією корисності.
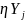 Окрім ресурсних обмежень, представлених
вектором A, враховують також обмеження
юридичні, психологічні, соціальні тощо,
представлені у нашому випадку вектором
B.
Ще
раз зазначимо, що усі ці функції, вектори
і характеристики визначають на етапі
здійснення постановки задачі.
Окрім ресурсних обмежень, представлених
вектором A, враховують також обмеження
юридичні, психологічні, соціальні тощо,
представлені у нашому випадку вектором
B.
Ще
раз зазначимо, що усі ці функції, вектори
і характеристики визначають на етапі
здійснення постановки задачі.
Суть
пошуку рішення полягає у визначенні
оптимального значення вектора
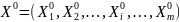 ,
тобто такого, який
забезпечує
розвиток проблемної ситуації у напрямі
обраних цілей з максимальним ефектом.
,
тобто такого, який
забезпечує
розвиток проблемної ситуації у напрямі
обраних цілей з максимальним ефектом.
Економіко-математична модель прийняття рішення в умовах певної невизначеності матиме вигляд:
-
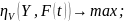 (3.1)
(3.1)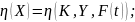 (3.5)
(3.5)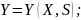 (3.2)
(3.2)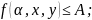 (3.6)
(3.6)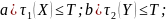 (3.3)
(3.3)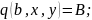 (3.7)
(3.7)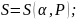 (3.4)
(3.4)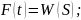 (3.8)
(3.8)
Дамо певні пояснення до наведеної моделі. Цільова функція (3.3) виражає сумарну корисність обраних альтернатив результатів дій і обраної системи цілей.
Рівність (3.4) відображає залежність альтернатив результатів дій від керованих чинників і станів зовнішнього середовища.
Обмеження
(3.5) може мати два варіанти:(3.5,а) - функція
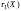 відображає
час отримання рішення X,
який залежить від отримання всієї
інформації, необхідної для постановки
задачі і здійснення процедури вироблення
рішення; якщо відомий час отримання
кожної компоненти
Xi,
то очевидним є представлення цієї умови
у такому вигляді:
відображає
час отримання рішення X,
який залежить від отримання всієї
інформації, необхідної для постановки
задачі і здійснення процедури вироблення
рішення; якщо відомий час отримання
кожної компоненти
Xi,
то очевидним є представлення цієї умови
у такому вигляді:
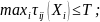 варіант
(3.5, b) вимагає врахування функцією
часу
вироблення рішення і виконання вибраних
варіантів дій у тому випадку, коли
величина Т
має
відповідний зміст.
варіант
(3.5, b) вимагає врахування функцією
часу
вироблення рішення і виконання вибраних
варіантів дій у тому випадку, коли
величина Т
має
відповідний зміст.
Рівність (3.6) відображає функціональну залежність станів зовнішнього середовища від імовірності їхнього настання та некерованих чинників, через які відбувається вплив зовнішнього середовища на проблемну ситуацію.
Корисність рішення X як функція, що залежить від критеріїв оцінки альтернатив, результатів дій і системи цілей, описане рівністю (3.7). Умова (b) враховує обмеженість ресурсів, витрати яких залежать від рішення х , альтернатив результатів дій ¥ і технологій А.
Умова
(3.9) відображає вплив зовнішнього
середовища у вигляді витратних функцій
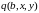 ,
аргументами яких є уже перелічені X,Y,
а
також технологічні коефіцієнти витрат
B.
,
аргументами яких є уже перелічені X,Y,
а
також технологічні коефіцієнти витрат
B.
Залежність (3.10) вказує на те, що цілі залежать від станів S і цю залежність описано функцією W(S).
Базова модель прийняття рішень (3.2) - (3.10) можна використовувати з метою забезпечення управлінської роботи на різних рівнях економічної системи. Зауважимо: чим нижчий рівень управління, тим більша частка таких задач, у яких фактично нескінченною є кількість варіантів дій. Аналогічно змінюється і число альтернатив станів зовнішнього середовища. Така модель дає змогу ефективно розмежовувати місце і роль засобів і технологій на окремих етапах в процесі прийняття рішень.
