
- •Глава 3. Теплогенерация в магнитном поле
- •3.1. Физические основы электромагнитной теплогенерации
- •3.2. Конструкции и принципы расчета индукторов
- •3.2.1. Установки для поверхностной закалки
- •3.3. Установки для сквозного нагрева
- •4. Теплогенерация в электрической дуге
- •4.1. Теоретические основы возникновения электрической дуги
- •4.2. Особенности дуги постоянного и переменного тока
- •5.3. Электрическая дуга как источник тепловой энергии
- •4.4. Особенности горения дуги в вакууме
Глава 3. Теплогенерация в магнитном поле
3.1. Физические основы электромагнитной теплогенерации
Физическая сущность индукционного нагрева заключается в том, что в материале, помещенном в переменное электромагнитное поле, возникает вихревое электрическое поле, электродвижущая сила которого i прямо пропорциональна скорости изменения магнитного потока Ф во времени
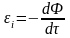 .
.
Под его воздействием носители электрических зарядов приходят в движение, образуя вихревые токи, вызывающие разогрев проводящей среды.
Электромагнитное поле создают индуктором, представляющим собой многовитковую цилиндрическую катушку (соленоид), выполненную из медной профилированной трубки, охлаждаемую водой. Через индуктор пропускают переменный электрический ток, в результате чего вокруг индуктора возникает изменяющееся во времени переменное магнитное поле. Это первое превращение электромагнитного поля.
Нагреваемый материал помещают внутрь индуктора. Изменяющийся поток магнитной индукции, созданный соленоидом, пронизывает нагреваемый материал и индуктирует в нем электрическое поле. Линии напряженности этого поля расположены в плоскости, перпендикулярной направлению магнитного потока, и имеют замкнутый контур. Под действием электрического поля в материале возникают токи проводимости, носящие вихревой характер. Это второе превращение энергии электромагнитного поля.
Энергия индуцированного переменного электрического поля в нагреваемом материале необратимо переходит в тепловую. Подобное тепловое рассеивание энергии определяется возникновением в материале вихревых токов. Благодаря выделяющейся теплоте материал нагревается. Это третье превращение энергии электромагнитного поля, причем энергетическое соотношение этого превращения описывается законом Джоуля – Ленца
 ,
,
где q – интенсивность объемной теплогенерации; – удельное электрическое сопротивление; Е – напряженность электрического поля.
На величину напряженности вихревого электрического поля в нагреваемом материале влияет частота питающего тока, т.е. частота изменений во времени магнитного потока. Отсутствие замкнутого магнитопровода в индукционных установках значительно увеличивает магнитный поток рассеяния. Число магнитных силовых линий, пронизывающих нагреваемый материал, будет очень мало, а это обстоятельство требует соответствующего увеличения частоты изменения во времени электромагнитного поля. Вот почему для эффективной работы индукционных установок необходимо использовать токи повышенной, а в остальных случаях и высокой частоты.
Рассмотрим участок бесконечно длинной электромагнитной системы, представляющей сплошной металлический цилиндр с однородными по объему свойствами, помещенный в поле цилиндрического индуктора, обтекаемого переменным синусоидальным током. Возникающая на поверхности индуктора цилиндрическая электромагнитная волна падает на боковую поверхность металла и несет энергию, величина которой определяется вектором Умова–Пойтинга. Среднее (за период) значение вектора потока энергии, проникающей через единицу боковой поверхности металла, определятся выражением
 ,
(3.1)
,
(3.1)
где
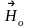 и
и
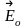 – векторы напряженности соответственной
магнитного и электрического полей у
поверхности металлического цилиндра,
являющиеся комплексными величинами.
– векторы напряженности соответственной
магнитного и электрического полей у
поверхности металлического цилиндра,
являющиеся комплексными величинами.
Для того чтобы получить среднее (по модулю) значение |S| в любой точке внутри цилиндра (т.е. распределение по радиусу внутренних источников тепла), необходимо в выражение (3.1) подставить модульные значения |Н| (r) и |Е| (r) в соответствующей точке.
Распределение напряженностей электрического и магнитного полей в толще металла, представленное на рис., было получено в результате решения уравнений электромагнитного поля (уравнений Максвелла), записанных в дифференциальной форме. По оси ординат отложены абсолютные значения модулей |Н| и |Е|, отнесенные к модулям |Но| и |Ео| на поверхности, а по оси абсцисс – отношение текущего радиуса r к радиусу цилиндра R2. При этом аргументом является относительный радиус нагреваемого цилиндра
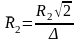 ,
(3.2)
,
(3.2)
где – величина, имеющая размерность длины и характеризующая степень затухания электромагнитного поля в металле по мере проникновения в глубь. Эту величину принято называть глубиной проникновения тока. Согласно теории электромагнитного поля для плоского массивного проводника
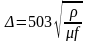 ,
(3.3)
,
(3.3)
которое показывает, что затухание поля зависит от частоты поля f, удельного электрического сопротивления и магнитной проницаемости металла .
С точки зрения физики процесса причиной затухания электромагнитной волны является превращение энергии электромагнитного поля в тепловую энергию, вследствие чего и происходит нагрев проводника.
Поскольку плотность
тока
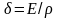 ,
то кривые рис.б дают также и картину
затухания плотности тока. Для цилиндра
с большой величиной относительного
радиуса
,
то кривые рис.б дают также и картину
затухания плотности тока. Для цилиндра
с большой величиной относительного
радиуса
 (а также и для пластины относительно
большой толщины) уменьшение плотности
тока от поверхности вглубь проводника
на расстояние х происходит по
экспериментальному закону
(а также и для пластины относительно
большой толщины) уменьшение плотности
тока от поверхности вглубь проводника
на расстояние х происходит по
экспериментальному закону
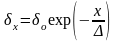 ,
(3.4)
,
(3.4)
где о – действующее значение плотности тока на поверхности.
Отмеченное неравномерное распределение плотности тока по сечению проводника (так называемый поверхностный эффект) существенно затрудняет выполнение электрических и тепловых расчетов при индукционном нагреве. Поэтому для практических расчетов было принято, что в пределах выделяется вся тепловая энергия в результате прохождения электромагнитной энергии через поверхность тела. В действительности, как показывают расчеты, в слое толщиной выделяется 86,5% всей мощности, проникающей в металл, а остальное количество тепла проходит в более глубокие его слои.
В дальнейшем все величины, относящиеся к индуктору, будем обозначать индексом «1», к нагреваемой садке – индексом «2» и к воздушному зазору между индуктором и садкой – индексом «3».
Приведенный на рис. 2 характер изменения Н и Е позволяет найти поток электромагнитной энергии S в любой точке нагреваемого цилиндра. Окончательно выражение для S запишется в виде
 ,
(3.5)
,
(3.5)
где Но – максимальное (амплитудное) значение напряженности магнитного поля; а и р – вспомогательные функции, представленные на рисунке 3.
При

 .
.
Поскольку Sо является величиной комплексной, в результате решения (3.1) получаются две составляющие энергии: действительная часть вектора дает величину потока активной энергии, выделяемой в металле в виде тепла
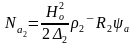 ,
(3.6)
,
(3.6)
а мнимая часть – величину рассеяния потока энергии переменного магнитного поля (реактивной энергии)
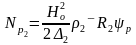 .
(3.7)
.
(3.7)
Если известна
действующая сила тока I1
в индукторе с числом витков 1,
то переходя от амплитудных Но к
действующим значениям Н (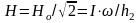 ),
после простых преобразований получим
следующие выражения для активной и
реактивной мощностей в нагреваемой
цилиндрической садке высотой h2
),
после простых преобразований получим
следующие выражения для активной и
реактивной мощностей в нагреваемой
цилиндрической садке высотой h2
 ,
(3.8)
,
(3.8)
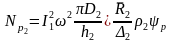 .
(3.9)
.
(3.9)
Поскольку активная, реактивная и полная мощность могут быть выражены через силу тока и сопротивление
 ,
,
становится возможным записать выражения для определения активного, реактивного и полного сопротивлений цилиндрической садки:
 (3.10)
(3.10)
Индуктор, создающий электромагнитное поле, чаще всего наматывают из медной трубки, образуя катушку (соленоид) с числом витков , между которыми наносится изоляция толщиной bиз. При высоте индуцирующего провода (трубки) hтр толщина изоляции учитывается коэффициентом заполнения индуктора
 .
(3.11)
.
(3.11)
Для многовиткового индуктора высотой h1 с числом витков и коэффициентом заполнения kз.и. при протекании по нему тока I1 теория электромагнитного поля дает следующие выражения для расчета активной мощности, теряемой в индукторе
 ,
(3.12)
,
(3.12)
и реактивной мощности в металле индуктора
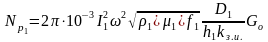 ,
(3.13)
,
(3.13)
где
Fo и
Go –
вспомогательные функции от аргумента
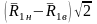 ,
приведенные на рис.4.
,
приведенные на рис.4.
График
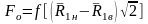 на рис.4 позволяет найти оптимальное
значение толщины индуцирующего провода,
обеспечивающее минимум электрических
потерь в индукторе. Функция Fo
имеет минимум при
;
откуда с учетом аналогичного выражения
(3.2), получим
на рис.4 позволяет найти оптимальное
значение толщины индуцирующего провода,
обеспечивающее минимум электрических
потерь в индукторе. Функция Fo
имеет минимум при
;
откуда с учетом аналогичного выражения
(3.2), получим
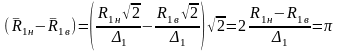 ,
,
и оптимальная толщина индуцирующего провода
 .
(3.14)
.
(3.14)
Поскольку индуктор выполняется из водоохлаждаемых полых трубок, под bи.опт следует понимать толщину стенки трубки, обращенную к нагреваемой заготовке, а не весь радиальный размер трубки.
При выполнении условия bи1,571 активное r1 и реактивное х1 сопротивления индуктора примерно равны и могут быть определены по выражению
 ,
(3.15)
,
(3.15)
где
 – расчетный диаметр индуктора.
– расчетный диаметр индуктора.
Коэффициент полезного действия индукционной установки для нагрева металла
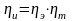 ,
,
где э – электрический КПД; т – термический КПД.
Под электрическим
КПД системы индуктор – загрузка понимают
отношение активной мощности, выделяющейся
в садке
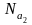 ,
к суммарной активной мощности индуцирующей
системы, складывающейся из мощности
и
активных потерь в индукторе
,
к суммарной активной мощности индуцирующей
системы, складывающейся из мощности
и
активных потерь в индукторе
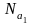 ,
т.е.
,
т.е.
 .
(3.16)
.
(3.16)
С учетом выражений 3.8 и 3.12 для случая нагрева сплошного цилиндра при допущении, что h2h1.
 .
(3.17)
.
(3.17)
На рисунке показан
характер зависимости электрического
КПД в функции относительного радиуса
нагреваемого цилиндра
(для условий нагрева стального цилиндра
с
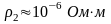 и 2=1, что
соответствует его температуре около
850 оС, медным индуктором с
и 2=1, что
соответствует его температуре около
850 оС, медным индуктором с
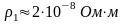 и 2=1). Как
видно, э в
сильной степени зависит от
в диапазоне 0<
<2.
Полагая, что точка перегиба кривых
соответствует значению
=2,5,
можно оценить минимальное значение
частоты электромагнитного поля fmin,
Гц допустимое с точки зрения нагрева.
и 2=1). Как
видно, э в
сильной степени зависит от
в диапазоне 0<
<2.
Полагая, что точка перегиба кривых
соответствует значению
=2,5,
можно оценить минимальное значение
частоты электромагнитного поля fmin,
Гц допустимое с точки зрения нагрева.
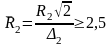 ,
или
,
или
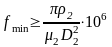 .
(3.18)
.
(3.18)
Анализ выражения (3.18) показывает, что на величину э оказывают влияние конструктивные параметры индукционной установки и физические свойства нагреваемых материалов и материала индуктора.
С уменьшением
зазора между индуктором и металлом (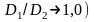 э
увеличивается. При конструировании
длинных индукторов необходимо обеспечивать
более высокие значения коэффициента
заполнения kз.и.
индуктора.
э
увеличивается. При конструировании
длинных индукторов необходимо обеспечивать
более высокие значения коэффициента
заполнения kз.и.
индуктора.
Наиболее целесообразно нагревать сплавы металлов, особенно ферромагнитные, как имеющие высокое удельное электрическое сопротивление 2. С другой стороны, сам индуктор обычно выполняют из меди (немагнитного материла с 1=1 и низким удельным электрическим сопротивлением 1).
Из выражения (3.18) также следует, что для достижения высокого КПД при снижении диаметра нагреваемой заготовки частота должна повышаться. Так, при D2=0,2м достаточно высокое значение э достигается при f150-200Гц, при D2=0,1м величина f600-800Гц и при D2=0,02 м f=7-8 кГц.
Под термическим КПД понимают отношение
 ,
(3.19)
,
(3.19)
где Nм – полезная мощность, выделяемая в металле; Nпот – мощность тепловых потерь всей установкой.
Величина активной мощности, поглощаемая нагреваемой заготовкой, определяется выражением (3.8)
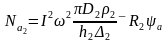 .
.
Поскольку при ярко
выраженном поверхностном эффекте
произведение
 ,
а также используя в выражении (3.8) вместо
2 его значение
из формулы (3.1), получим
,
а также используя в выражении (3.8) вместо
2 его значение
из формулы (3.1), получим
 .
(3.20)
.
(3.20)
Здесь К – коэффициент,
обобщающий неменяющиеся величины в
(3.8) в процессе нагрева, а выражение
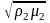 часто называют коэффициентом поглощения
мощности, поскольку он характеризует
интенсивность поглощения электромагнитной
энергии садкой в зависимости от ее
свойств. Свойства эти меняются при
нагреве садки по мере повышения ее
температуры. Относительная магнитная
проницаемость 2
для ферромагнитных материалов при
изменении температуры от комнатной до
650-700 оС меняется мало, а затем при
достижении определенной температуры
750-800 оС, называемой точкой Кюри,
она падает скачком до величины, равной
магнитной проницаемости вакуума =1
(приведенные значения 2
для стали соответствуют малым значениям
Но10-4
А/м). При этом удельное электрическое
сопротивление возрастает примерно в 5
раз. Соответственно этому глубина
проникновения тока 2,
при переходе через точку Кюри резко
возрастает (в 10 раз) и для стали, потерявшей
магнитные свойства, ее называют горячей
глубиной проникновения тока. Подставив
в выражение (3.3) значения =к=10-6
часто называют коэффициентом поглощения
мощности, поскольку он характеризует
интенсивность поглощения электромагнитной
энергии садкой в зависимости от ее
свойств. Свойства эти меняются при
нагреве садки по мере повышения ее
температуры. Относительная магнитная
проницаемость 2
для ферромагнитных материалов при
изменении температуры от комнатной до
650-700 оС меняется мало, а затем при
достижении определенной температуры
750-800 оС, называемой точкой Кюри,
она падает скачком до величины, равной
магнитной проницаемости вакуума =1
(приведенные значения 2
для стали соответствуют малым значениям
Но10-4
А/м). При этом удельное электрическое
сопротивление возрастает примерно в 5
раз. Соответственно этому глубина
проникновения тока 2,
при переходе через точку Кюри резко
возрастает (в 10 раз) и для стали, потерявшей
магнитные свойства, ее называют горячей
глубиной проникновения тока. Подставив
в выражение (3.3) значения =к=10-6
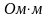 и =1 получим
и =1 получим
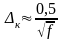 ,
м. (3.21)
,
м. (3.21)
Индекс «к» указывает, что значение соответствующих величин относится к температуре выше точки Кюри.
Прогреваясь от слоя к слою, от поверхности внутрь, сталь теряет свои магнитные свойства, в результате чего характер распределения плотности тока резко меняется; металл становится как бы двухслойным. Поверхностный слой, прогретый выше температуры магнитного превращения стали, толщиной хк имеет более равномерное распределение плотности тока, а следовательно, и равномерное выделение энергии в нем. В остальной массе металла, не потерявшей магнитные свойства, плотность тока резко убывает, характеризуя существенное снижение выделяемой энергии. Если задаваемая величина прогреваемого слоя металла хк<к, то будет иметь место глубинный режим нагрева, используемый при закалке металла. Если хк>к, то тепло в глубь металла передается, главным образом, теплопроводностью и данный режим нагрева называется поверхностным. Время нагрева, при том же перепаде температуры в нагреваемом слое, резко увеличивается и примерно соответствует нагреву с внешними источниками тепла.
