23. Баланс потужностей.

У будь-якому електричному колі активна потужність, що генерується джерелами, дорівнює активній потужності, яка споживається всіма приймачами (навантаженнями). Можна показати, що і сума реактивних потужностей, які віддаються, дорівнює сумі реактивних потужностей, що споживаються.

Для електричного кола, що містить q вузлів, можна записати за першим законом Кірхгофа (q-1) рівняння:

,  ;

де позитивні напрями всіх струмів прийняті від k-го вузла до вузлів - 1, 2, 3,...q.

Помножимо кожне з цих рівнянь на комплексне значення напруги з позитивним напрямом від відповідного вузла до q-го вузла та додамо ці добутки:

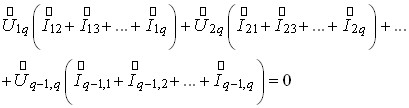
З урахуванням того, що    будемо мати:

Сума контурних потужностей, спожитих всіма витками електричного кола, дорівнює нулю. Отже, дорівнюють нулю алгебраїчні суми дійсних та уявних частин потужностей (тобто активних та реактивних потужностей).

Оскільки від’ємні потужності є потужностями, що віддаються (вважали, що   та   співпадають за напрямом), то звідси і витікає закон балансу як активних, так і реактивних потужностей.

24. Частина електричного кола, яка розглядається по відношенню до будь-яких двох пар її виводів,називається чотириполюсником.

Коефіцієнти чотириполюсників

Чотириполюсник можна охарактеризувати напругами та струмами на його виводах:  .

Довільну пару цих величин можна вважати незалежною а іншу пару – залежною. Співвідношення між напругами та струмами на вході та виході чотириполюсника можуть бути описані в вигляді шести різних систем (форм) рівнянь: Y, Z, A, B, H, G (число сполучень з 4-х по два). Для кожної системи рівнянь (параметрів чотириполюсника) є своя найбільш придатна область застосування, яка визначається структурою кола, значеннями елементів та способами з’єднання виводів з зовнішнім колом.

Y – форма запису рівнянь чотириполюсника

Нехай незалежними змінними є   та  , а залежними – струми  . Система рівнянь буде мати такий вигляд:

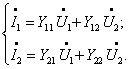
Для систем Y, Z, H, G форми за позитивні напрями струмів та напруг прийняті такі, що відповідають прямій передачі. Коефіцієнти рівнянь комплексні, але крапки ставити не прийнято.

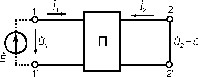
Параметри чотириполюсників доцільно визначати, використовуючи режим короткого замикання.

Нехай ?? (к. з. на виході).

При цьому:

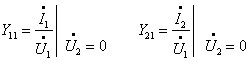
Якщо підключити джерело до виводів 2 – 2’, а 1 – 1’ закоротити, отримаємо:

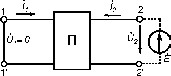
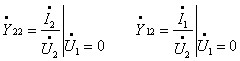
У загальному випадку чотириполюсник характеризується чотирма коефіцієнтами.

Для оборотних чотириполюсників за умови     , буде лише три незалежних коефіцієнта.

Визначимо умови симетричності чотириполюсника. Розглянемо чотириполюсник зі зворотною передачею сигналів. Підставимо   в Y – систему рівнянь замість ,  ,   :

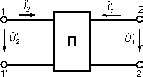
   або 

Для симетричних чотириполюсників буде тільки два незалежних коефіцієнта, оскільки Y11 = Y22 (з-за умови симетрії чотириполюсника).

Рівняння чотириполюсників звичайно записують у матричній формі:

.

Z – форма запису рівнянь чотириполюсника

Виразимо напруги , через струми . Знайдемо розв’язок системи Y - параметрів:

  .

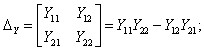
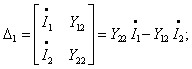
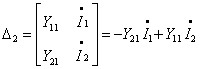Тоді будемо мати:

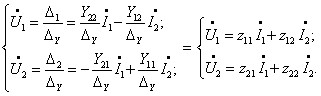
Отримали зв’язок між «Y» та «z» параметрами чотириполюсників:

.

Для того, щоб коефіцієнти однієї форми визначити через коефіцієнти іншої форми, необхідно виразити які-небудь дві однакові величини у цих формах запису та порівняти їх. Зв’язок між різними параметрами чотириполюсників подають у вигляді таблиць.

- параметри чотириполюсників можна легко визначити з дослідів у режимі холостого ходу:

.

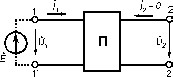
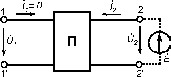
Y11 та z11, Y22 та z22 не є взаємно оберненими величинами, тому що вони визначаються для різних режимів (к. з., та х.х.)

z12 = z21 - умова оборотності;

z11 = z22 - умова симетрії.

У матричній формі: 

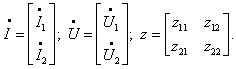
А – форма запису рівнянь чотириполюсника

Позитивні напрямки струмів та напруг відповідають указаним на рисунку.

Визначимо з системи «Y» – форми , через , . Для цього з другого рівняння знаходимо та підставляємо у перше рівняння:

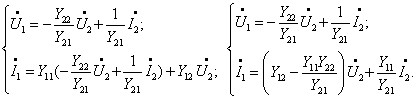
З урахуванням напрямку струму будемо мати:

.

У матричній формі:

 

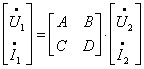
«А» - форма запису рівнянь.

Визначник системи

;

Y12 = Y21 - для оборотних чотириполюсників.

Умова оборотності чотириполюсників через коефіцієнти «А» форми:

AD – BC = 1.

Умова симетрії: А = D.

Параметри «А» форми чотириполюсників також можна визначити з дослідів холостого ходу та короткого замикання:

 

       .

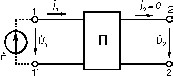
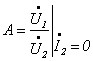
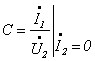
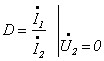Інші системи рівнянь мають вигляд:

     

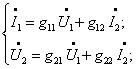
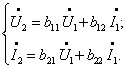
H - форма G - форма B - форма

25. Параметри холостого ходу та короткого замикання

Коефіцієнти Y11 та Y22 є вхідними провідностями чотириполюсника, визначеними зліва та справа при замкнених протилежних виводах. Відповідно z11 та z22 є вхідними опорами чотириполюсника при розімкнених виводах. Таким чином можемо записати:

.

Цих параметрів достатньо для складання рівнянь оборотного чотириполюсника, тому що тільки три з них є незалежними. У загальному випадку для опису необоротного чотириполюсника параметрів холостого ходу та короткого замикання вже недостатньо. Покажемо, що лише три з чотирьох параметрів незалежні.

.

Звідси отримуємо рівність:

. 

Таким чином будь-який з параметрів холостого ходу та короткого замикання можна виразити через три інших.

Якщо чотириполюсник симетричний, то  , тобто він характеризується лише двома параметрами.

Параметри холостого ходу та короткого замикання можуть бути виражені через будь-яку систему коефіцієнтів чотириполюсника, наприклад через «А» – параметри:

.

В свою чергу будь-яка система коефіцієнтів оборотного чотириполюсника може бути виражена через параметри холостого ходу та короткого замикання.

Наприклад:

,

або             .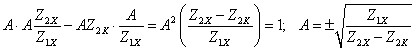

Для коефіцієнта А можуть бути знаки «+» або «-» в залежності від позитивних напрямів струмів та напруг.

Схеми заміщення чотириполюсників

На базі рівнянь чотириполюсника можуть бути побудовані різні схеми заміщення, які полегшують дослідження загальних властивостей розглядуваного кола.

На практиці найбільш часто використовують «Т» або «П» – подібні схеми заміщення. Спочатку розглянемо схеми заміщення оборотних чотириполюсників (містять лише пасивні елементи).

 

 

Схеми заміщення оборотних чотириполюсників

Виразимо параметри схеми заміщення  через «А» коефіцієнти чотириполюсника. Записуємо рівняння А – форми для «Т» – подібної схеми:

             .

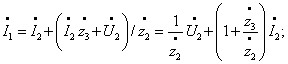
Тобто можна записати:

Звідси маємо:

.

Тоді для  буде мати місце:

.

Параметри  можна визначити через коефіцієнти «Z» – форми (струм  має протилежний відносно позначеного на рисунку напрямок):

      

.

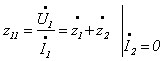
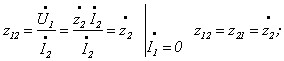
Тоді будемо мати :

.

Аналогічно можна виразити параметри «Т» – подібної схеми через інші системи «Y», «H», «G», «B».

Розглянемо «П» – подібну систему заміщення.

 

.

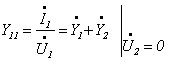
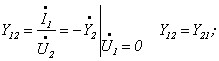
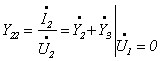Тоді будемо мати

.

Пасивний П-подібний чотириполюсник може бути перетворений у Т-подібний (або навпаки) за правилом перетворення трикутника в еквівалентну зірку.

Треба відзначити, що П та Т-подібні схеми заміщення чотириполюсників, які містять реактивні елементи, фізично можна реалізувати тільки тоді, коли параметри R, L, Сдодатні. Чотириполюсник без реактивних елементів завжди фізично можна реалізувати.